- Research Article
- Open access
- Published:
Combined Data Association and Evolving Particle Filter for Tracking of Multiple Articulated Objects
EURASIP Journal on Image and Video Processing volume 2011, Article number: 642532 (2011)
Abstract
This paper proposes an approach for tracking multiple articulated targets using a combined data association and evolving population particle filter. A visual target is represented as a pictorial structure using a collection of parts together with a model of their geometry. Tracking multiple targets in video involves an iterative alternating scheme of selecting valid measurements belonging to a target from a clutter or other measurements that all fall within a validation gate. An algorithm with extended likelihood probabilistic data association and evolving groups of populations of particles representing a multiple-part distribution is designed. Variety in the particles is introduced using constrained genetic operators both in the sampling and resampling steps. We explore the effect of various model parameters on system performance and show that the proposed model achieves better accuracy than other widely used methods on standard datasets.
1. Introduction
Tracking articulated targets is a central problem in computer vision, with applications including robotics and surveillance. The problem of multiple articulated target tracking (MATT) deals with tracking a variable number of targets, each consisting of the same number of different constituent body parts, given noisy measurements at every instant of time from a dynamic scene, and simultaneously maintaining correct target identities irrespective of any visual perturbations [1–4]. However, these tasks are complicated by the nonrigid variation within the general class of objects that we wish to track (e.g., people, animals, etc.), appearance variations of targets, and the presence of occlusions. Different methods have been proposed in the literature to cope with these challenges, for example, [2, 5–7]. The pictorial structure approach proposed in [6] is an appealing approach for people modelling in view its simplicity and generality. A different, limb-based structure model is developed in [5], particularly suited for the detection and tracking of multiple people in crowded scenes.
The problem of MATT can be divided into the subproblems of estimation and data association. A popular approach to solving this estimation problem is to build linearised filters such as the extended Kalman filter (EKF) [8], under a Gaussian noise assumption. Consequently, sufficient statistics from such linearised filters are used for data association. However, with nonlinear models in the state equation and non-Gaussian noise assumption, such linearised models often lead to inaccurate solutions or even face divergence. The sequential Monte Carlo (SMC) methods, such as the particle filters (PFs) [9] have proven their potential for the estimation of nonlinear systems, with non-Gaussian noise assumption and multimodal distributions.
In this paper, we propose an approach combining evolving population particle filtering with extended likelihood data association for MATT applications. To account for the uncertainty in the origin of the measurement, the extended likelihood data association method [10] incorporates local attribute information of measurements weighted by probabilistic data association (PDA) for correctly identifying the measurement from the target as against the clutter. On the other hand, the evolving population particle filter, provides iterative convergence of groups of particles through a specified kernel by introducing variety in the population using constrained genetic operators in both the sampling and resampling steps.
One of the main novelties of the method is that it conveniently integrates data association into evolving population particle filtering, thus allowing particles to regenerate both in sampling and resampling steps by simultaneously disregarding particle measurement that account for clutter within a specified validation gate. Our results suggest that the proposed integrated approach can considerably improve performance when compared individually to a Markov chain Monte Carlo (MCMC) combined data association technique or a generic particle filter (non-MCMC filter). Second, the geometrical constraints imposed by the picture structure representing the target are intrinsically modeled into the particle regeneration process through constrained genetic operations. Furthermore, some of the system parameters (such as the size of the validation gate) are learned from the data rather than specified by hand.
The remaining part of the paper is organised in the following way. Section 2 makes an overview of related works. Section 3 presents the proposed approach for multiple articulated object tracking. Results are given in Section 4. Finally, conclusions are summarised in Section 5.
2. Related Work
MATT is a highly challenging area of research within computer vision and tracking communities. The high degree of freedom of multiple articulated regions together with the interdependencies between them and with other targets requires efficient techniques able to cope effectively with the dynamic changes of the objects. In general, motion tracking of articulated objects in video consists of two distinct steps: detection and tracking. During the detection process, we aim to segment the human objects and their constituent body parts from the frames of the video sequences. In tracking, we are spatially locating these detected regions in time. A number of techniques have been proposed for the detection and tracking phases [2, 11–13]. In our paper, we assume a standard procedure applied for the detection step and propose a novel tracking methodology.
Tracking in recent years is often considered as a dynamic system estimation problem [14]. A number of different techniques have been proposed [15] in the past to estimate the variables of such dynamic systems. Some of the important methods include the Kalman filter [16], and unscented Kalman filter [17]. These methods assume that the posterior probability density of the system model is Gaussian. This assumption is more often restrictive and does not always suit different applications. In order to cope with the nonlinearity, extended techniques such as unscented Kalman filter [18], extended Kalman filter [19], approximation grid filter, and particle filters [17, 20] have been recommended. A particle filter approximates the posterior state probability density using a set of particles and propagating these particles over time with appropriate weighting coefficients often produces efficient tracking. Particle filters are robust to nonlinear, non-Gaussian systems with multi-modal distributions. However, even with a large population of particles, there may be no or little number of particles near the actual correct state. The second main drawback of particle filter methods is degeneracy. The problem of degeneracy refers to some particles having negligible weight as against the weight being concentrated on few others. Resampling techniques are employed to tackle degeneracy issues but sometimes when applied improperly can lead to sample impoverishment [21].
Population-based methods [22–24] are techniques that generate a collection of samples in parallel as against single independent or dependent samples. We can conveniently categorize these population-based methods into (a) MCMC type of methods and (b) methods based on importance sampling and resampling ideas. While MCMC methods are directed by theoretical convergence based on iterations, sampling/resampling techniques rely on processing a number of samples in parallel and sequential Monte. The population MCMC methods apply population moves that exchange variables between population members in order to generate the new target density. An example of a population move is the exchange move that swaps information between chains in a population. Similar types of moves are realised in the genetic algorithms, with the crossover, mutation, and exchange steps. In contrast, the sequential Monte Carlo methods [25] were constructed to sample from a sequence of related target distributions, using resampling techniques on the samples from previous target density. Commonly used resampling techniques include multinomial resampling [26], residual resampling technique [25], and stratified resampling [25].
One of the other main issues of MATT applications is the presence of multiple parts of the body and multiple targets that share similar feature characteristics, thus leading to uncertainty in the origin of measurements. Data association (DA) methods [27, 28] are used for correctly identifying the measurement that originated from the target from clutter of other multiple noisy measurements. It is assumed that the clutter is a model of false detections whose statistical properties are significantly different from those of the targets. Data association is of crucial importance to our problem because of the requirement to relate each measurement to the correct body part of the correct object of interest. There has been extensive studies in data association [10, 27, 29–36]. Most methods are restricted by assumptions on the number of targets, statistical properties of observations, and number of possible measurements.
In order to tackle the problem of MATT, it is important to combine estimation techniques and data association so that robust tracking is possible.
3. The Combined Data Association with Evolving Population Particle Filter for Multiple Articulated Object Tracking
In our proposed technique, we formulate MATT as an estimation problem combined with data association. Let us begin by denoting the total number of targets in our scene to be  . We represent each target
. We represent each target  as a pictorial structure using a collection of
as a pictorial structure using a collection of  parts as in [6]. The objective of the proposed technique is to estimate the state vector
parts as in [6]. The objective of the proposed technique is to estimate the state vector  of each target
of each target  at time instant
at time instant  by recursively updating the posterior distribution of each target
by recursively updating the posterior distribution of each target  based on a set
based on a set  of measurements at time
of measurements at time  . The movement of each target is described by a general nonlinear state space model and estimated using the prediction step:
. The movement of each target is described by a general nonlinear state space model and estimated using the prediction step:

and update/filtering step

where,  is the dynamic model of state evolution and
is the dynamic model of state evolution and  is the likelihood of any measurement
is the likelihood of any measurement  given the state
given the state  .
.
The proposed technique is meant to track multiple targets by taking into consideration the geometrical constraints of the various parts which represents the target before evaluating the marginal distribution. An evolving population Markov chain Monte Carlo (EPMCMC) filter is developed that encapsulates constrained evolution of the populations using specific genetic operators and robust association of measurements to targets incorporating local attribute information using the expected likelihood data association method [10]. The developed approach can be summarised as follows:
-
(1)
initialisation: using pictorial structure type models as in [7], we localise all the
 targets along with the configuration of their
targets along with the configuration of their  parts,
parts, -
(2)
for iterations
 ,
,-
(a)
evolve particles using constrained genetic operators as in EPMCMC filter,
-
(b)
the expected likelihood data association provides an efficient solution for data association of each object into the particle weights of the EPMCMC filter.
-
(a)
In the following sections, we describe the two steps in detail before outlining how they are integrated within the proposed framework.
3.1. EPMCMC Filter
The EPMCMC filter algorithm proceeds in three distinct steps. The first step involves initialising the populations of particles from their respective proposal distributions. Let  ,
,  represent the population of particles for target
represent the population of particles for target  (each particle is a configuration vector containing the position and speed of the
(each particle is a configuration vector containing the position and speed of the  body parts for the target) at time instant
body parts for the target) at time instant  . So, during initialisation:
. So, during initialisation: 

 , where
, where  is the distribution of particles around the initial localisation of different body parts of target
is the distribution of particles around the initial localisation of different body parts of target  . During initialisation, we also evaluate the initial weights of particles
. During initialisation, we also evaluate the initial weights of particles  and normalise the weights to get
and normalise the weights to get  .
.
The EPMCMC filter iterates between the resampling and sampling steps. The resampling step is usually performed only when the effective sample size (ESS) is less than a predefined threshold  and is measured as
and is measured as  . During the resampling step, we perform local evolution of particles; that is, particles from the same population belonging to the same part of the target are combined iteratively using steps of crossover, mutation, or exchange. This approach introduces variety in particles by regenerating a unique and good population. Here, we also recalculate weights of particles in each population using a relevant likelihood metric and normalise them. An illustration of the genetic moves involved in the EPMCMC filter is presented in Figure 1.
. During the resampling step, we perform local evolution of particles; that is, particles from the same population belonging to the same part of the target are combined iteratively using steps of crossover, mutation, or exchange. This approach introduces variety in particles by regenerating a unique and good population. Here, we also recalculate weights of particles in each population using a relevant likelihood metric and normalise them. An illustration of the genetic moves involved in the EPMCMC filter is presented in Figure 1.
In the sampling step, we perform global evolution of particles, that is, iteratively evolving particles from different populations belonging to different parts of the target using the steps of crossover, mutation, or exchange. However, the main difference from local evolution of particles is that in the global evolution we enforce geometrical constraints into the evolution, process. These geometrical constraints are derived from the pictorial structure model of the target and are based on the neighbourhood structure of every part of the target. When subjecting the particles to evolution using genetic operators, we allow particles of one part to be influenced by only the particles of its neighbours. For example, when performing the crossover operation, between two particles  and
and  , we crossover chromosomes only based on the neighbourhood relationships that parts share with each other. That is, we restrict crossovers between the arms of one particle to the legs of the other and encourage crossovers between arms of one part together with the torso of the other, as these are neighbouring regions of the elastic pictorial structure model.
, we crossover chromosomes only based on the neighbourhood relationships that parts share with each other. That is, we restrict crossovers between the arms of one particle to the legs of the other and encourage crossovers between arms of one part together with the torso of the other, as these are neighbouring regions of the elastic pictorial structure model.
In addition, we evaluate the likelihood of each particle based on how well the image data supports the proposed hypothesized candidate parts. We map this support as the weighted summation of two subsequent terms: the first one indicates the goodness of fit of the part with the image data, and the second one measures the goodness of fit of pairs of candidate parts as connected in the pictorial structure model.
The proposed EPMCMC filter is given in Algorithm 1, the population MCMC move is presented in Algorithm 2, and the details for each step of the genetic algorithm (crossover, mutation, and exchange) are given in the next subsection.
Algorithm 1: The proposed evolving population Markov chain Monte Carlo filter.
-
(1)
Initialisation: at
 generate initial samples
generate initial samples  and their respective weights
and their respective weights 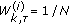 .
. -
(2)
Sampling
-
(i)
For
 .
. -
(ii)
For each sample
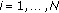 .
.Draw
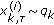 , where
, where  is the
is the  th sample at
th sample at  th time instant and
th time instant and  is a known transition prior at time
is a known transition prior at timeinstant
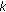 .
. -
(iii)
Move the populations of samples by
 , using the genetic transition kernel
, using the genetic transition kernel 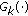 according to
according tocrossover, mutation or exchange steps as described below.
-
(iv)
Evaluate weights
 from the likelihood as presented in the next subsection and normalise the weights
from the likelihood as presented in the next subsection and normalise the weightsto obtain
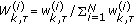 .
.
-
(i)
-
(3)
Resampling
-
(i)
If
 , where the
, where the 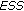 is measured as
is measured as 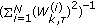 and
and  is some threshold.
is some threshold.-
(a)
For
 iterations
iterations-
(a1)
Resample using one of the standard resampling techniques such as residual resampling.
-
(a2)
Perform population MCMC based moves to samples as mentioned in Section 3.1.1.
-
(a3)
Recompute the weights
 and normalise the weights to obtain
and normalise the weights to obtain  .
.
-
(a1)
-
(b)
End
-
(a)
-
(ii)
Increment the time instant
 .
. -
(iii)
Iterate steps (2). and (3).
-
(i)
Algorithm 2: Population MCMC moves.
-
(1)
Initialisation
-
(i)
Select
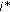 resampled particles from each population
resampled particles from each population 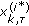 , where
, where 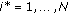 .
.
-
(i)
-
(2)
Iterate steps (2) and (3).
-
(3)
-
(a)
Mutation
Perform Mutation as illustrated in Section 3.1.3.
-
(b)
CrossOver or Exchange Move Perform CrossOver or Exchange moves as illustrated in Section 3.1.2 or Section 3.1.4, respectively. Accept the move based on the Metropolis-Hastings rule, for example, from the probability
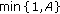 as described in Section 3.1.4.
as described in Section 3.1.4.
-
(a)
3.1.1. Resample Moves
In the resample move step, equally weighted particles are chosen, and population MCMC is applied. We summarise the population MCMC algorithm as shown in Algorithm 2.
3.1.2. Crossver
In the proposed framework, the state vector is represented as a string of bits. The crossover point  is a random point on the string of bits of length
is a random point on the string of bits of length  . The crossover operator cannot be applied to all parts of the state vector. Some parts of the state vector may not undergo any changes, and thus for such components, the probability of crossover
. The crossover operator cannot be applied to all parts of the state vector. Some parts of the state vector may not undergo any changes, and thus for such components, the probability of crossover  is zero. This leaves the crossover being operated only on components that are expected to undergo random changes. The crossover operator functions on two distinguished offsprings (paired particles), for example,
is zero. This leaves the crossover being operated only on components that are expected to undergo random changes. The crossover operator functions on two distinguished offsprings (paired particles), for example,  ,
,  . The algorithm for crossover is described below:
. The algorithm for crossover is described below:
-
(i)
draw a uniform random number
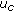 for every component
for every component 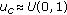 , and if
, and if 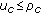 , then perform crossover,
, then perform crossover, -
(ii)
(ii)estimate a crossover point
 based on a uniform random integer between 1 and the length of the component
based on a uniform random integer between 1 and the length of the component  ,
, -
(iii)
generate two offsprings
 (3)
(3)
where  and
and  refers to the length of the samples
refers to the length of the samples  and
and  , respectively.
, respectively.
For simplicity in the remaining derivation, we will omit the index  . For crossover, the proposal distribution
. For crossover, the proposal distribution  can be expressed as a product of the proposals for the two offsprings
can be expressed as a product of the proposals for the two offsprings

Then, in the crossover operation, performed with the two offsprings  and
and  , the particle weight can be expressed in the form
, the particle weight can be expressed in the form

Then, the recursive weights can be written as

Here,  is the likelihood function for the
is the likelihood function for the  th offspring,
th offspring,  is the likelihood function of the
is the likelihood function of the  th offspring and
th offspring and  and
and  are the weights at
are the weights at  th time instant, for the
th time instant, for the  th and
th and  th offspring, respectively.
th offspring, respectively.
Hence, in the case of the crossover, where there are paired particles with the same weight, we marginalise one of them and express the weights as a function of the proposal PDF of the other PDF.
3.1.3. Mutation
A probability of mutation  is initially defined for each component. Such a probability is chosen in order to make sure that components that need no stochastic fluctuations could be prohibited from undergoing mutation operation. For such components, the probability of mutation
is initially defined for each component. Such a probability is chosen in order to make sure that components that need no stochastic fluctuations could be prohibited from undergoing mutation operation. For such components, the probability of mutation  is considered zero. The components are assumed as a vector string of binary units. According to the proposed mutation mechanism,
is considered zero. The components are assumed as a vector string of binary units. According to the proposed mutation mechanism,
-
(i)
draw a uniform random number
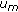 for every component
for every component 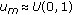 , and if
, and if 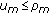 , then perform mutation,
, then perform mutation, -
(ii)
(ii)estimate a mutation point
 based on a uniform random integer between 1 and length of the component
based on a uniform random integer between 1 and length of the component  ,
, -
(iii)
flip the mutation point
 .
.
The weights are of the form

where,  is a uniform random number. During mutation, samples that undergo mutation are mutually independent. Therefore, the updated proposal distribution at time
is a uniform random number. During mutation, samples that undergo mutation are mutually independent. Therefore, the updated proposal distribution at time  is a factor of the proposal distribution at the previous iteration
is a factor of the proposal distribution at the previous iteration  .
.
3.1.4. Exchange
Consider two independent chains of samples, for example,  and
and  . For their target distributions
. For their target distributions  and
and  , respectively, the swap of information between these two chains can be performed with a Metropolis-Hastings step. The swap occurs with probability
, respectively, the swap of information between these two chains can be performed with a Metropolis-Hastings step. The swap occurs with probability  , where
, where

The genetic transition kernel combines the effectiveness of samples between various populations to create more efficient groups of samples.
3.2. Expected Likelihood Probabilistic Data Association (ELPDA)
Since the state vector  for target
for target  consists of the states for all body parts
consists of the states for all body parts  , a data association problem needs to be resolved. In our work, we adopt the expected likelihood data association method from [10]. For the set of available measurements, we assume that one of the measurements originates from the target, and the rest are due to spurious clutter. In the case of tracking the pictorial structure of the human target, colour histograms are used for matching and the corresponding measurement equation is highly nonlinear. The data association problem is considered with respect to the whole pictorial structure (the whole graph) representing the target, for example, with respect to
, a data association problem needs to be resolved. In our work, we adopt the expected likelihood data association method from [10]. For the set of available measurements, we assume that one of the measurements originates from the target, and the rest are due to spurious clutter. In the case of tracking the pictorial structure of the human target, colour histograms are used for matching and the corresponding measurement equation is highly nonlinear. The data association problem is considered with respect to the whole pictorial structure (the whole graph) representing the target, for example, with respect to  .
.
We adapt the weights of particles  in the move step of the EPMCMC filter specified in Section 3.1.
in the move step of the EPMCMC filter specified in Section 3.1.
Let  denote the number of available measurements at time step
denote the number of available measurements at time step  . The measurements at time step
. The measurements at time step  are denoted as
are denoted as  , where
, where  . If
. If  denotes any association event, then
denotes any association event, then  is a particular association event that assigns the
is a particular association event that assigns the  th measurement to target
th measurement to target  . According to [10], the conditional probability density function
. According to [10], the conditional probability density function  of the association event
of the association event  that the
that the  th measurement within the validation gate is the measurement that originated from the target is given by
th measurement within the validation gate is the measurement that originated from the target is given by

for the set of  measurements
measurements  that fall within the validation gate. We expand the conditional probability from above using the Bayesian rule to get
that fall within the validation gate. We expand the conditional probability from above using the Bayesian rule to get

If the incorrect measurements have a uniform probability density function within the gating volume  , and with the assumption of a normal measurement error for a correct measurement, we can rewrite
, and with the assumption of a normal measurement error for a correct measurement, we can rewrite

where  is the probability of gating,
is the probability of gating,  is the covariance matrix of the innovation vector
is the covariance matrix of the innovation vector  . Finally, it has been shown [10] that the probability
. Finally, it has been shown [10] that the probability  of association events can be computed as
of association events can be computed as

where  is the detection probability,
is the detection probability,  is the probability mass function of the number of incorrect measurements,
is the probability mass function of the number of incorrect measurements,  refers to the probability that a target is detected and its measurements fall within the gate, and
refers to the probability that a target is detected and its measurements fall within the gate, and  is the measurement error covariance matrix.
is the measurement error covariance matrix.
Finally, we approximate the weights of the particles based on the computed expected likelihood using

where  .
.
4. Results
In this section, we perform systematic experiments evaluating (1) the accuracy of our proposed EPMCMC + ELPDA method with the EPMCMC + PDA algorithm and with a generic particle filter framework with a joint probabilistic data association (JPDA PF) proposed in [37, 38] and (2) the influence of the system parameters on the model including the geometric constraints, number of parts being tracked, the radius of the validation gate. We demonstrate our results on videos containing human targets, where the pictorial structure of the target is modeled as a graphical model of the parts of the body. The transition prior is assumed to be a constant velocity model [8] applied jointly with the pictorial structure for each target. The pictorial structure is represented as rectangles for each body part, and the state vector consists of the position and speed for the centre of each body part. To evaluate the performance of the models, we compute the root mean square error distance (RMSE) between the estimated center point of every part and its manually labeled counterpart. The results are presented in the form of a cumulative RMSE for all the targets in the video.
4.1. Multiple People Tracking
To track multiple people (together with their multiple body parts) in video, we use the CAVIAR [39] data set sequences. The CAVIAR dataset contains over 80 video sequences with one or more targets moving in real-time scenarios. We have chosen 11 videos from the data set at varying levels of complexity in terms of the motion characteristics, occlusion, and clutter (due to illumination changes). We have further divided the 11 selected sequences in 17 short clips with varying number of targets. Table 1 elaborates on the chosen sequences and the clips that have been extracted from these sequences along with the details of the frames, number of targets, the level of occlusion, and the presence of clutter. The tracked people have been manually annotated in these clips using a maximum 10-point model consisting of the centers of the head (1 point), torso (1 point), arms (2 points for each arm), and legs (2 points for each leg). We would like to particular highlight that the frames are of resolution 384 × 288 captured at 25 frames per second. The scales of the human targets are fairly small in comparison with the resolution of the image, and thus in some of the images, a 10-point model gives a dense set of labeled ground-truth which is unusable; therefore, in such sequences, we use a 6-point model. We use the method of [7, 40] to initialise the multiple body parts composed multiple targets in first frame of each video using the pictorial structure model. For all our experiment described below unless mentioned otherwise, the number of Monte Carlo cycles is fixed to 100, the number of particles used is 500, and the size of the validation gate is 15. All our experiments are conducted on an Intel Duo Core processor with 3 GB RAM.
4.2. Comparison of Proposed with Related Techniques
One of the main novelties of the proposed EPMCMC + ELPDA method is its integration of expected likelihood into the weights of EPMCMC. The following experiments compares the accuracy of the proposed algorithm with the combined EPMCMC and PDA filter. We present the trajectories of two targets tracked by both techniques in Figure 3 and sample image frames from the corresponding tracked torso of the two targets in Figure 2. We also present some sample image frames of tracked torso's of multiple targets (four targets) from a different video sequence in Figure 4. The combined RMSE curves (in Figures 5 and 6) indicates that our technique has better accuracy than the baseline method. The mean combined RMSE values recorded for increasing Monte Carlo cycles are 2.5369 and 4.2667 for target 1 and 3.2547 and 4.3737 for target 2 using the proposed and baseline strategies, respectively. In terms of the computational demand, our algorithm takes 3419 msec on an average per image frame as against the combined EPMCMC and PDA methods that take 2169 msec (implemented in MATLAB). This is mainly due to the computation of the expected likelihood of all measurements that fall within the validation gate. We have also found that the cumulative error in the localisation of the target reduces by approximately 39% for an increased 1.2 seconds in the processing time. We presume that the tradeoff between the time taken for processing as against the accuracy of our technique acceptably good. A detailed analysis of the computation time per image frame across various different video clips is summarised in Table 1.
Trajectory of multiple targets (a) using proposed method (red/blue), (b) using baseline method (magenta/black) and (c) using Non-MCMC baseline method (green/blue), the JPDA PF proposed in [37, 38]. Proposed method (EPMCMC + ELPDA) outputBaseline method (EPMCMC + PDA) outputNon-MCMC baseline method (JPDA PF) output
4.3. Effect of Changing System Parameters
We study the effect of different changing system parameters and compare them between the proposed EPMCMC + ELPDA and the EPMCMC + PDA model. We do not compare our results to the generic particle filter framework, as these parameters are particularly relevant to the parts-based models. First, we examine the effect of increasing the number of targets being tracked on the performance of the models. Figure 7 suggests that increasing the number of targets from 1 to 2 decreases the accuracy of the proposed EPMCMC + ELPDA model, but increasing the targets beyond this does not significantly alter its accuracy.
Secondly, we investigate the effect of increasing the number of parts of each target that is used for tracking. In the lower levels of the model, we have a smaller collection of more salient parts representing the target followed by increasing number of lesser important parts. In the following experiment, we examine the impact of increasing the number of parts representing the target by comparing the model with level one (1 part: torso), level two (2 parts: head and torso), level three (6 parts: head, torso, two hands, and two legs), and level four (10 parts-head, torso, four for hands, and four for legs). The plot in Figure 8 suggests that increasing the representation of the target (using a larger subset of parts) increases accuracy.
In Figure 9, we present the results showing the effect of increasing the size of the validation gate against the accuracy of EPMCMC + ELPDA technique. The cumulative RMSE curves demonstrating the effect of increasing the size of the validation gate indicate that with increase gate size, accuracy increases, but beyond this, it does not improve the performance further.
Finally, in Figure 10, we demonstrate the effect of geometric constraints being enforced in the measurement of the likelihood against the accuracy of EPMCMC + ELPDA technique. The cumulative RMSE curves prove beyond doubt that with appropriate geometrical constraints on the pictorial structure model accuracy increases.
4.4. Failure Modes
In this subsection, we highlight some of common failure modes of the proposed framework. We attribute the missed detections of our proposed framework to three main conditions. First, when the object(s) of interest are subject to a high degree of self occlusion due to articulation of body parts, our framework fails to match the pictorial structure well to the image data and subsequently fail during tracking. The illustrations in Figure 11(a) show a scenario from our test set, where tracking multiple body parts accurately was highly difficult due to the aforementioned conditions. In such test sequences, we have resorted to models containing lower number of distinguishable body parts. In Figure 11(b), we highlight the second mode of failures that are mainly caused due to rapid changes in illumination conditions. Finally, we also describe conditions such as the image acquisition perspective and scale of the object(s) of interest as other causes for missed detections in Figure 11(c).
Failure modes of the proposed EPMCMC + ELPDA model: (a) complex occlusion example; (b) rapid change in illumination conditions; (c) image acquisition perspectives. Complex occlusion of body parts of a single targetObject navigating in areas with rapid illumination changesChanging the image acquisition perspective and small object scale
5. Conclusion
We have proposed an innovative method for combining extended likelihood data association with evolving population particle filtering for robust and accurate multiple target tracking. The evolving population filter introduces variety in the population of particles by combining them in both the sampling and resampling steps using constrained genetic operations. The extended likelihood data association filters those measurements that belong to the target from a clutter of other noisy measurements analysed within the validation gate. System parameters such the radius of validation gate are reestimated during each iteration, rather than fixed empirically, resulting in a model that outperforms similar recent methods on standard datasets.
References
Aggarwal JK, Cai Q: Human motion analysis: a review. Computer Vision and Image Understanding 1999, 73(3):428-440. 10.1006/cviu.1998.0744
Forsyth DA, Arikan O, Ikemoto L, O'Brien J, Ramanan D: Computational studies of human motion: part 1, tracking and motion synthesis. Foundations and Trends in Computer Graphics and Vision 2006, 1(2-3):77-254.
Gavrila DM: The visual analysis of human movement: a survey. Computer Vision and Image Understanding 1999, 73(1):82-98. 10.1006/cviu.1998.0716
Moeslund TB, Granum E: A survey of computer vision-based human motion capture. Computer Vision and Image Understanding 2001, 81(3):231-268. 10.1006/cviu.2000.0897
Andriluka M, Roth S, Schiele B: People-tracking-by-detection and people-detection-by-tracking. Proceedings of the 26th IEEE Conference on Computer Vision and Pattern Recognition (CVPR '08), June 2008
Felzenszwalb PF, Huttenlocher DP: Pictorial structures for object recognition. International Journal of Computer Vision 2005, 61(1):55-79.
Ramanan D, Forsyth DA, Zisserman A: Tracking people by learning their appearance. IEEE Transactions on Pattern Analysis and Machine Intelligence 2007, 29(1):65-81.
Bar-Shalom Y, Li XR: Estimation and Tracking: Principles,Techniques and Software. Artech House, Norwood, Mass, USA; 1993.
Ristic B, Arulampalam S, Gordon N: Beyond the Kalman Filter: Particle Filter for Tracking Applications. Artech House, London, UK; 2004.
Marrs A, Maskell S, Bar-Shalom Y: Expected likelihood for tracking in clutter with particle filters. Signal and data Processing of Small Targets, April 2002, Proceedings of SPIE 4728: 230-239.
Cucchiara R, Grana C, Piccardi M, Prati A: Detecting moving objects, ghosts, and shadows in video streams. IEEE Transactions on Pattern Analysis and Machine Intelligence 2003, 25(10):1337-1342. 10.1109/TPAMI.2003.1233909
Gerónimo D, López AM, Sappa AD, Graf T: Survey of pedestrian detection for advanced driver assistance systems. IEEE Transactions on Pattern Analysis and Machine Intelligence 2010, 32(7):1239-1258.
Yilmaz A, Javed O, Shah M: Object tracking: a survey. ACM Computing Surveys 2006., 38(4):
Zhou S, Chellappa R, Moghaddam B: Adaptive visual tracking and recognition using particle filters. Proceedings of the IEEE International Conference on Multimedia & Expo (ICME '03), July 2003 560-566.
Gandhi T, Trivedi MM: Pedestrian protection systems: issues, survey, and challenges. IEEE Transactions on Intelligent Transportation Systems 2007, 8(3):413-430.
Jung S, Wohn K: Tracking and motion estimation of the articulated object: a hierarchical Kalman filter approach. Real-Time Imaging 1997, 3(6):415-432. 10.1006/rtim.1997.0078
Ristic B, Arulampalam S, Gordon N: Beyond the Kalman Filter: Particle Filter for Tracking Applications. Volume 2. Artech House, Norwood, Mass, USA; 2004.
Briers M, Maskell S, Wright R: A Rao-Blackwellised unscented Kalman filter. In Proceedings of the 6th International Conference on Information Fusion, 2003, Queensland, Australia. ISIF; 55-61.
Bizup D, Brown D: The over-extended Kalman filter—use it! In Proceedings of the 6th International Conference on Information Fusion, 2003, Queensland, Australia. ISIF; 40-46.
Schultz D, Fox D, Hightower J: People tracking with anonimous and ID-sensors using Rao-Blackwellised particle filters. Proceedings of the International Conference on Artificial Intelligence (IJCAI '03), 2003
Wan E, van der Merwe R: The unscented Kalman filter. In Kalman Filtering and Neural Networks. Edited by: Haykin S. John Wiley & Sons, New York, NY, USA; 2001:221-280.
Cappé O, Guillin A, Marin JM, Robert CP: Population monte carlo. Journal of Computational and Graphical Statistics 2004, 13(4):907-929. 10.1198/106186004X12803
Iba Y, Coffa S: Population-based monte carlo algorithms. Journal of Computational and Graphical Statistics 2000, 13(4):157-1933.
Jasra A, Stephens DA, Holmes CC: On population-based simulation for static inference. Statistics and Computing 2007, 17(3):263-279. 10.1007/s11222-007-9028-9
Cappe O, Douc R, Moulines E: Comparison of resampling schemes for particle filtering. Proceedings of the 4th International Symposiumon Image and Signal Processing and Analysis (ISPA '05), 2005, Croatia
Hol J, Shön T, Gustaffsson F: On resampling algorithms for particlefilters. Proceedings of the Nonlinear Statistical Signal Processing Workshop, September, 2006, Cambridge, UK
Blackman S, Popoli R: Design and Analysis of Modern Tracking Systems. Artech House Radar Library; 1999.
Salmond D, Fisher D, Gordon N: Tracking and identification forclosely spaced objects in clutter. In Proceedings of the European Control Conference, July 1997, Brussels, Belgium. IEEE;
Kirubarajan T, Bar-Shalom Y: Probabilistic data association techniques for target tracking in clutter. Proceedings of the IEEE 2004, 92(3):536-556. 10.1109/JPROC.2003.823149
Li XR: Engineer's guide to variable-structure multiple-model estimation for tracking. In Multitarget-Multisensor Tracking: Applications and Advances. Volume 3. Edited by: Bar-Shalom Y, Blair WD. Artech House, Norwood, Mass, USA; 2002:499-567.
Maskell S, Rollason M, Gordon N, Salmond D: Efficient particle filtering for multiple target tracking with application to tracking in structured images. Image and Vision Computing 2003, 21(10):931-939. 10.1016/S0262-8856(03)00087-8
Bar-Shalom Y, Dale Blair W: Multitarget-Multisensor Tracking: Applications and Advances. Volume 3. Artech House, Norwood, Mass, USA; 2000.
Briers M, Maskell S, Philpott M: Two-dimensional assignment with merged measurements using Lagrangian relaxation. Signal Processing of Small Targets, 2003, Proceedings of SPIE 283-292.
Horridge P, Maskell S: Real-time tracking of hundreds of targets with efficient exact JPDAF implementation. Proceedings of International Conference on Information Fusion, 2006
Maskell S, Briers M, Wright R: Fast mutual exclusion. Signal Processing of Small Targets, 2004, Proceedings of SPIE
Pao LY: Multisensor multitarget mixture reduction algorithms for tracking. Journal of Guidance, Control, and Dynamics 1994, 17(6):1205-1211. 10.2514/3.21334
Jaward MH, Mihaylova L, Canagarajah N, Bull D: A data association algorithm for multiple object tracking in video sequences. Proceedings of the IEE Seminar on Target Tracking: Algorithms and Applications, 2006, Birmingham, UK 131-136.
Jaward MH, Mihaylova L, Canagarajah N, Bull D: Multiple objectstracking using particle filters in video sequences. Proceedings of the IEEE Aerospace Conference, 2006, Big Sky, Mont, USA
CAVIAR test case scenarios 2005, http://homepages.inf.ed.ac.uk/rbf/
Ramanan D, Forsyth DA: Finding and tracking people from the bottom up. Proceedings of the IEEE Computer Society Conference on Computer Vision and Pattern Recognition (CCVPR '03), June 2003 467-474.
Acknowledgments
The authors acknowledge the support of UK MOD Data and Information Fusion Defence Technology Centre under the Tracking Cluster Project no. DIFDTC/CSIPC1/02. The authors would also like to sincerely thank Professor Simon Godsill for his useful advices and discussions on sequential population Monte Carlo methods. They acknowledge the support from the (European Community's) Seventh Framework Programme (FP7/2007–2013) under Grant no. 238710 (Monte Carlo-based Innovative Management and Processing for an Unrivalled Leap in Sensor Exploitation).
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Bhaskar, H., Mihaylova, L. Combined Data Association and Evolving Particle Filter for Tracking of Multiple Articulated Objects. J Image Video Proc. 2011, 642532 (2011). https://doi.org/10.1155/2011/642532
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1155/2011/642532
 targets along with the configuration of their
targets along with the configuration of their  parts,
parts, ,
,
 generate initial samples
generate initial samples  and their respective weights
and their respective weights 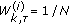 .
. .
.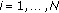 .
.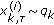 , where
, where  is the
is the  th sample at
th sample at  th time instant and
th time instant and  is a known transition prior at time
is a known transition prior at time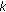 .
. , using the genetic transition kernel
, using the genetic transition kernel 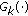 according to
according to from the likelihood as presented in the next subsection and normalise the weights
from the likelihood as presented in the next subsection and normalise the weights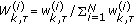 .
. , where the
, where the 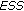 is measured as
is measured as 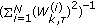 and
and  is some threshold.
is some threshold. iterations
iterations and normalise the weights to obtain
and normalise the weights to obtain  .
. .
. resampled particles from each population
resampled particles from each population  , where
, where 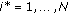 .
.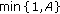 as described in Section 3.1.4.
as described in Section 3.1.4.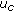 for every component
for every component 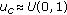 , and if
, and if 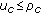 , then perform crossover,
, then perform crossover, based on a uniform random integer between 1 and the length of the component
based on a uniform random integer between 1 and the length of the component  ,
,
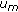 for every component
for every component 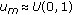 , and if
, and if 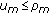 , then perform mutation,
, then perform mutation, based on a uniform random integer between 1 and length of the component
based on a uniform random integer between 1 and length of the component  ,
, .
.








