- Research Article
- Open access
- Published:
Texture Classification for 3D Urban Map
EURASIP Journal on Image and Video Processing volume 2009, Article number: 432853 (2009)
Abstract
This paper proposes a method to control texture resolution for rendering large-scale 3D urban maps. Since on the 3D maps texture data generally tend to be far larger than geometry information such as vertices and triangles, it is more effective to reduce the texture by exploiting the LOD (Level of Detail) in order to decrease whole data size. For this purpose, we propose a new method to control the resolution of the texture. In our method we classify the textures to four classes based on their salient features. The appropriate texture resolutions are decided based on the classification resulsts, their rendered sizes on a display, and their level of importance. We verify the validity of our texture classification algorithm by applying it to the large-scale 3D urban map rendering.
1. Introduction
Three-dimensional urban maps (3D map) have a variety of applications such as navigation systems and disaster management and simulations of urban planning. As the technology that acquires 3D range data and models of cities from the real world has advanced [1–4], more sophisticated visualization of photo-realistic 3D map is becoming available.
In general the 3D map has geometry information of 3D meshes and texture images. Since the amount of the data is huge, its data size often becomes a problem when it is treated in devices including PCs, car-navigation systems, and portable devices. Therefore, the reduction in the volume of data becomes important to make the 3D map applications user friendly.
Many methods on the LOD control of general 3D models have been proposed so far [5–7]. Moreover there exist some visualization techniques [7–12] of terrain data that express the surfaces of a ground with geographical features like mountain district. While these conventional methods assume that a single model is locally smooth and consists of topological manifold that contains a large number of meshes, the city model consists chiefly of buildings. Since the data in the 3D map mostly consist of many small, already simplified meshes (like buildings made of some cuboids), these simplification methods cannot be applied to it. Although some methods on modeling and rendering of the 3D maps have been already proposed [13–15], there exist few methods concerning the reduction of the texture data for the 3D map. In the 3D map, the proportion of the total amount of texture data tends to be much higher than that of geometrical information such as vertices and triangles. For example, in the 3D map we use for a simulation (Figure 10) the whole size of the textures is 461 MBytes in JPEG format, while the geometry information has only 15 MBytes in gzipped VRML. It means that the LOD of the texture has a capability of effectively reducing the whole data size rather than the LOD of the geometry. For this purpose, we propose the technique for controlling the resolution of the texture. Wang et al. [16] propose a method to detect the repetition of content in the textures to reduce storage and required memory. In this paper we focus on urban map rendering from a ground level (as shown in Figure 11) rather than bird's eye view. These systems can be used in car-navigation and human-navigation systems.
In the following sections, we describe the overview of our rendering system with consideration of the level of texture importance. In Section 3, we propose our classification method based on K-Nearest Neighbor approach. Then we show some experimental results to verify the validity of our classification method in Section 4. In Section 5 we summarize the strength of our method.
2. Proposed Method
2.1. Outline
Our 3D map is composed of simplified polygonal meshes (as shown in Figure 3) and textures mapped on the meshes. The textures are made of photographs of real scenes.
In order to reduce rendering cost, it is an efficient stategy that only visible data from a user's viewpoint are loaded and rendered. To implement this, we introduce a representative viewpoint (RV), which is a discrete point in the 3D map used for a reference point of rendering. In our rendering system, we spread RVs all over the map in advance. Using the Z-buffer algorithm, visible objects from each RV are determined. When rendering, we first find the RV closest to a current viewpoint of a user. The objects seen from the RV on the map are found, and then only the visible objects from it are rendered.
To further reuduce the rendering cost, we introduce a method to determine an appropriate resolution for texture. In the framework of our rendering system, first of all, a set of images at multiple resolutions is prepared for all the texture images beforehand. Our strategy is that an appropriate resolution is found for each texture, and the texture at the resolution is loaded. The appropriate resolution is determined for each texture image by two criteria "Level" and "Class". The former considers a look from a specific viewpoint, and the latter evaluates importance of the texture, which we will explain in Section 3. The entire algorithm is depicted in Figure 1.
Note that in our setting, different types of objects are separately saved to different image files, for example, no image includes a billboard and a window simultaneously. Since our classification is done for images directly, the algorithm would fail for images that simultaneously contain objects to be classified to different classes.
2.2. Selection of Representative Viewpoints
In this step we select the representative viewpoints (RVs) on the 3D map. In our framework, we suppose that a user walks on a street of the 3D map. Only rendering from a ground level is considered. Although to make the points equally spaced in the map, one has to define them based on the geometrical form of terrain data, we adopt the following simple procedure to reduce its computational complexity, as we assume the terrain associated with the map is flat.
To select the RVs, the entire map is divided into rectangle areas, and then we set the points on the grids as candidates for the RVs. Figure 2 shows an example of the RVs (note that in actual cases the distance between the lattice points is shorter, and the points are more densely located).
Next, the points in the area thought to be paths when the user actually walks through in the 3D map are selected as the RVs from the candidates on the lattice points in Figure 2. This is done simply by excluding the candidate points in high places such as the tops of the buildings.
2.3. Determination of Visible Objects
A set of the objects that are visible from each of the RVs are determined by using the Z-buffer algorithm [17]. The accuracy of the determination depends on the resolution of the Z-buffer. Increasing the resolution, both of the accuracy and the computational cost increase, and vice versa. We have determined the resolution of the buffer by trial and error. Note that one needs to do this processing to a 3D map only once as preprocessing. For example, Figure 3 depicts the objects judged as "visible" from the RV denoted by the sphere in the middle. The determination is done for all the RVs, and we store the indices of the objects in a list.
2.4. Texture Resolution
In general there is a trade-off between the quality of the texture and its computational cost to load and render it. It is necessary to find an appropriate resolution of the texture that maintains an adequate image quality and low computational cost in order to enhance the efficiency in rendering the 3D map. The determination of the resolution is done for all the textures on the visible objects from each RV. Our previous work [18] defines the "Level" of the importance for each texture, and then based on the level we select an appropriate resolution for the texture among several resolutions prepared in advance. We determine the level by two criteria: (1) the size of the texture on a display and (2) the "look" of the texture. The size of the rendered texture is decided by the following three elements.
-
(i)
The distance
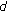 between the RV and the surface where the textures are mapped.
between the RV and the surface where the textures are mapped. -
(ii)
The area
 of the texture in the 3D map.
of the texture in the 3D map. -
(iii)
The number of repeats
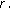
The distance  can be found by the barycentric coordinates of the surface where the texture is mapped and the
can be found by the barycentric coordinates of the surface where the texture is mapped and the  coordinates of the RV. When the surface is slant to the RV, the area of the texture is narrower than the one seen from the front. To take this into account, we first consider a virtual plane
coordinates of the RV. When the surface is slant to the RV, the area of the texture is narrower than the one seen from the front. To take this into account, we first consider a virtual plane  that is perpendicular to the line connecting center of the plane and the RV. The area
that is perpendicular to the line connecting center of the plane and the RV. The area  in the new surface made by projecting each vertex of the surface, where the texture is mapped, to the plane
in the new surface made by projecting each vertex of the surface, where the texture is mapped, to the plane  is calculated. Sometimes one texture is repeatedly mapped on a large surface. The number of the repeats
is calculated. Sometimes one texture is repeatedly mapped on a large surface. The number of the repeats  can be found by the texture coordinate
can be found by the texture coordinate  . Finally the size of the texture is estimated by using
. Finally the size of the texture is estimated by using  , and
, and  .
.
The "look" of the texture is evaluated by (1) the ratio of sharp edges in the texture and (2) the number of colors used in the texture. As for texture with sharp edges, one can easily identify what it is due to its recognizable feature in a real scene and is often used as markers in some applications such as a navigation system. Thus in our framework, we consider that such a texture has high level of importance. Conversely, for a texture without sharp edges the level of importance is considered low and low resolution is enough to express such texture. To distinguish these types of images, we first introduce the ratio of sharp edges. To actually evaluate the edges, first we calculate the intensity  from
from  values:
values:

Then, the edges are detected by applying the Laplacian filter to  . Two thresholds
. Two thresholds  and
and  (
( ) are prepared, and the number of pixels whose absolute values exceed each of the thresholds is counted. Denoting, the numbers of pixels that exceed
) are prepared, and the number of pixels whose absolute values exceed each of the thresholds is counted. Denoting, the numbers of pixels that exceed  and
and  as
as  and
and  respectively, the ratio of the sharp edges
respectively, the ratio of the sharp edges  is given by
is given by

The threshold  is used for saliency detection and
is used for saliency detection and  control a weight on images with smooth background. Of course the two thresholds affect the performance of the algorithm, for example, the smaller
control a weight on images with smooth background. Of course the two thresholds affect the performance of the algorithm, for example, the smaller  put more weights on images with flat background. However the thresholds do not sensitively affect a final result. We choose these thresholds by trial and error.
put more weights on images with flat background. However the thresholds do not sensitively affect a final result. We choose these thresholds by trial and error.
Next we consider the colors of the texture. In this method, the texture composed of the wide variety of colors is considered as "less important" texture, since in many applications including the navigation system, too complex information seldom plays an important role, and it is even unrecognizable from a distance. To evaluate the color complexity, we use the variance  of the RGB histograms. Note that as each bin of the histogram means its frequency, a low variance indicates that the texture contains a wide variety of colors and a small number of colors mean a high variance.
of the RGB histograms. Note that as each bin of the histogram means its frequency, a low variance indicates that the texture contains a wide variety of colors and a small number of colors mean a high variance.
Finally we simply combine the measures

where  is a normalization factor. We use this
is a normalization factor. We use this  for judging the level of importance of the texture.
for judging the level of importance of the texture.
3. Texture Classification
In the previous section, we define the value  that is obtained from the display size and the features of the texture. In our previous report [18], one of the multiple resolutions is assigned according to
that is obtained from the display size and the features of the texture. In our previous report [18], one of the multiple resolutions is assigned according to  of each texture, when actually rendering the 3D map. In the system of [18] , we prepare four levels of the textures, which are simply created by reducing the resolution of an original texture by 1/2, 1/4, 1/8. However with this method, salient texture such as road traffic signs and unremarkable texture like the walls of buildings are treated similarly. To address the problem, we introduce a new LOD control based on the texture classification. We make it possible to control the resolution more reasonably based on image features by classifying the texture into some classes, and then changing the reduction ratio based on the classes. By using this method it becomes possible to make the resolution of the image in one class smaller than the one in an other class even if it has larger
of each texture, when actually rendering the 3D map. In the system of [18] , we prepare four levels of the textures, which are simply created by reducing the resolution of an original texture by 1/2, 1/4, 1/8. However with this method, salient texture such as road traffic signs and unremarkable texture like the walls of buildings are treated similarly. To address the problem, we introduce a new LOD control based on the texture classification. We make it possible to control the resolution more reasonably based on image features by classifying the texture into some classes, and then changing the reduction ratio based on the classes. By using this method it becomes possible to make the resolution of the image in one class smaller than the one in an other class even if it has larger  in (3).
in (3).
3.1. Definition of Class
We first define some classes. Figure 4 shows some examples of the textures that are often used for walls of buildings. These textures mainly have soft edges, and their colors are apt to be saturated. As these types of textures have simple patterns, they rarely have remarkable meaning like letters and marks. Therefore a low resolution is often enough to maintain its visual quality in the 3D map.
On the other hand, the textures with sharp edges and vivid colors shown in Figure 5, unlike in Figure 4, have salient features, and often contain important information. They are often used as landmarks in the application of navigation system. Moreover, a human easily perceives blurring and ringing artifacts when the texture is rendered at a low resolution, which results in a decrease of visual quality. Thus a higher resolution should be allocated for this kind of the textures.
The texture that contains some sharp and soft edges simultaneously like in Figure 6 is located between those in Figures 4 and 5. In other words they are less simple than those in Figure 4 but also less significant than those in Figure 5. The low resolution display will somewhat decrease the quality of such textures. However it will not become a serious problem since those seldom contain significant features.
Some example of the fourth class is shown in Figure 7. The textures with minute and complex structures are not often used as markers and considered less important. And the visual quality of these images are not very much affected by reducing the resolution, since a masking effect of such complex images is higher than smooth images from a psychophysical point of view [19]. Moreover this kind of textures is less compressible due to its granularity, which is inefficient in terms of overall trade-off between data sizes and data visual quality.
In the end, we define the following four classes.
Class 1: walls with soft edges.
Class 2: texture with some clearly outlined objects with smooth background.
Class 3: walls with sharp edges.
Class 4: others.
In our framework, we select the resolution based on these classes besides the levels based on (3). We consider the case that four levels of textures are prepared, where the reduction ratios are 1, 1/2, 1/4, and 1/8, and all the textures are labeled as each of the Levels 1 to 4. Then we classify all of the original texture to Class 1 to 4. For the textures in Class 2, their original images are allocated to the Level 1 and 2 and the images shrunk to a half are allocated to other levels, while for Class 1 the images shrunk to 1/8 are used for all the levels. By this strategy, efficient LOD control of the texture is made possible than the case of only taking (3) into account.
3.2. Classification Method
The K-Nearest Neighbor (K-NN) algorithm is used to automatically classify a large amount of textures. In general the selection of feature vectors greatly affects the accuracy of the classification. Here we introduce two feature vectors based on colors and edges.
The first feature is color moments of color. The color moments have been widely used in conventional image retrieval systems [20, 21]. The first order moment (mean) roughly measures the appearance of images. Although it has been proved to be efficient in the retrieval system, in our application measuring the color difference does not improve this classification, that is, blue and red signboards should be equally treated. On the other hand, the second moment (variance) of the color measures the minuteness and has the capability of discriminating simplicity and complexity of the textures. The third (skewness) and forth (kurtosis) moments may also be applied, but these high-order moments are often sensitive to small changes and may degrade the performance. For the reasons stated above, we adopt the second-order moment for the feature of colors.
The choice of color space is also an important issue. The drawback of directly using the RGB pixel values is that the RGB color space lacks perceptual uniformity. Uniform color spaces such as CIE 1976  and
and  have been successfully used in some retrieval methods. However to transform the RGB space to these uniform spaces, the information of the three primaries and reference white are needed, since they are device independent. Instead the HSV is used in our system. The HSV is suitable for our application since it is easily translated from RGB, and color saturation plays an important role to evaluate the saliency of images. In the end, we calculate the variances of H, S, and V channels with respect to all the pixels, and then the three variances are adopted as the first feature. As the second element for the feature vector, we use the energy of edges derived by the anisotropic diffusion filter [22]. The anisotropic diffusion filter is an iterative nonlinear lowpass operator that flattens smooth regions while keeping sharp edges. At each iteration, one multiplies the weights called "edge-stopping function"
have been successfully used in some retrieval methods. However to transform the RGB space to these uniform spaces, the information of the three primaries and reference white are needed, since they are device independent. Instead the HSV is used in our system. The HSV is suitable for our application since it is easily translated from RGB, and color saturation plays an important role to evaluate the saliency of images. In the end, we calculate the variances of H, S, and V channels with respect to all the pixels, and then the three variances are adopted as the first feature. As the second element for the feature vector, we use the energy of edges derived by the anisotropic diffusion filter [22]. The anisotropic diffusion filter is an iterative nonlinear lowpass operator that flattens smooth regions while keeping sharp edges. At each iteration, one multiplies the weights called "edge-stopping function"  to the difference between a current pixel
to the difference between a current pixel  and its neighbors, and then it is added to the current pixel value. The output at each iteration is expressed by
and its neighbors, and then it is added to the current pixel value. The output at each iteration is expressed by

where  is an iteration number and
is an iteration number and  is a neighborhood of
is a neighborhood of  .
.  is a parameter that controls the smoothing effects. In [22], they introduce two functions for
is a parameter that controls the smoothing effects. In [22], they introduce two functions for  . We adopt one of them:
. We adopt one of them:

where  is a parameter that controls the strength of the edges to remain, and
is a parameter that controls the strength of the edges to remain, and  is the intensity of the edge at site
is the intensity of the edge at site  . When
. When  , the weight
, the weight  becomes small, which reduces the affects of smoothing. Oppositely when
becomes small, which reduces the affects of smoothing. Oppositely when  approaches to 1 and it reduces the difference from its neighbors. Figure 8 illustrates the effect of the anisotropic diffusion. After the operation, we calculate the difference between an original image
approaches to 1 and it reduces the difference from its neighbors. Figure 8 illustrates the effect of the anisotropic diffusion. After the operation, we calculate the difference between an original image  and its smoothed version
and its smoothed version  , and then we adopt the energy of the difference as the second feature
, and then we adopt the energy of the difference as the second feature  , that is,
, that is,

where  is the number of pixels. The role of the feature is to take only sharp edges into consideration.
is the number of pixels. The role of the feature is to take only sharp edges into consideration.
3.3. Rendering
By applying the pre-processing of Sections 2 and 3, all the objects that are visible from each RV are selected, and the classes and levels of all the texture for the RVs are determined. Then we construct the list of the RVs. In the list, each RV has the indices of all the visible objects and textures that belong to the objects. The class and level assigned to the texture are listed as in Figure 9.
When walking through the 3D map, a current position and its closest RV are found, and then loaded are all the textures at the appropriate resolutions that belong to the nine RVs, that is, closest RV and eight neighboring RVs. The reason why the neighboring RVs are loaded is that loading cost can be reduced and scenes can smoothly change when the user moves to the area of another RV.
4. Experimental Results
4.1. Precision of Classification
In our experiment, we use a 3D map with 5140 textures shown in Figure 10. For learning of the K-NN, 400 textures are used for the four classes, and we set  . To evaluate the validity of our classification method, we manually classify the textures to the four classes randomly select 50 textures in each class, and then use them as ground truth. Then, we count the numbers of correctly classified textures and calculate the precision of the classification by
. To evaluate the validity of our classification method, we manually classify the textures to the four classes randomly select 50 textures in each class, and then use them as ground truth. Then, we count the numbers of correctly classified textures and calculate the precision of the classification by

where  is the classes and
is the classes and  and
and  are the number of the textures that are correctly classified and are manually classified as the ground truth (in our experiment
are the number of the textures that are correctly classified and are manually classified as the ground truth (in our experiment  ), respectively. The precision for each class is defined as
), respectively. The precision for each class is defined as

First of all we verify the validity of our feature vector: the moment of the color and the edge energy based on the anisotropic diffusion. The feature vectors in our method are compared with features that are often used for general image retrieval [20, 21, 23–25]. Table 1 shows the comparison in color, as follows.
-
(i)
Var. Hist.: the variance of the color histogram.
-
(ii)
Hist(512): the color histogram quantized to 512 bins.
-
(iii)
CCV: color Coherent Vector proposed in [23].
-
(iv)
Moment: proposed feature vector.
In Table 2 we show the comparison in the features of edges, as follows.
-
(i)
Sharp edges: the cost in (2) that we use to determine the texture level.
-
(ii)
Wavelet coeffs.: quantized wavelet coefficients (high pass outputs of the dyadic wavelet).
-
(iii)
Directionality: the quantized direction of the edges that is obtained by Sobel filter.
-
(iv)
Anisotropic diffusion: proposed feature vector.
Among the feature vectors in colors, our method gives the highest score. For the edges, our method and the wavelet coefficients perform better than others. In Table 3, we show the precision of the combination of the two feature vectors. After experiments for every combination of the vectors in Tables 1 and 2, we have confirmed that our method outperforms others. Note that although it is possible to increase the dimension of vectors to add some features, we have seen little improvement with more vectors.
4.2. Data Size and Quality of 3D Map
We investigate the data size and the quality of the 3D map with and without our resolution control technique. In this experiment, we set the reduction ratio of the resolutions as in Table 4, where 1/2 means that the resolution is reduced by half both in rows and columns. Note that all the texture images are stored in JPEG format.
Figure 11 illustrates a snapshot of the 3D map from some viewpoint, in which our resolution control is not applied, that is, the textures at original resolutions are used. Figure 12 shows the result obtained by our resolution control with the reduction ratio of Table 4.
We adopt the Visual Difference Predictor (VDP) [26] to quantitatively evaluate the visual quality. The VDP is an image assessment tool that models some properties of the HVS, such as nonlinearity, frequency selectivity, direction selectivity, and masking. The VDP outputs a probability map that predicts a probability of error visibility for each pixel. Thus higher values represent that errors are more perceivable. The numerical comparison is shown in Table 5 when it is displayed at the resolutions of  and
and  . The values in VDP75 and VDP95 of this table indicate the ratio of pixels in percentage that have higher probability than 75% and 95% in the probability map. Thus only a few percentages of pixels may be perceptually different. The data size in Table 5 is the total sum of the texture data sizes to load and render for displaying Figures 11 and 12. In practice 25.8 % of data reduction is achieved. The total number of pixels to load can also be reduced by 25%. Note that, however, storage required by the algorithm is larger than the method without the data reduction by 87.5% since we need to prepare the textures of the sizes 1/2, 1/4, and 1/8 as well as the original textures. In the end, it can be seen from Figure 12 and Table 5 that we achieve a rendering quality without any significant visual loss while the amount of the data to load is reduced to one quarter. In other rendering examples we have tested, we have confirmed that our algorithm significantly reduces the data with little visual differences.
. The values in VDP75 and VDP95 of this table indicate the ratio of pixels in percentage that have higher probability than 75% and 95% in the probability map. Thus only a few percentages of pixels may be perceptually different. The data size in Table 5 is the total sum of the texture data sizes to load and render for displaying Figures 11 and 12. In practice 25.8 % of data reduction is achieved. The total number of pixels to load can also be reduced by 25%. Note that, however, storage required by the algorithm is larger than the method without the data reduction by 87.5% since we need to prepare the textures of the sizes 1/2, 1/4, and 1/8 as well as the original textures. In the end, it can be seen from Figure 12 and Table 5 that we achieve a rendering quality without any significant visual loss while the amount of the data to load is reduced to one quarter. In other rendering examples we have tested, we have confirmed that our algorithm significantly reduces the data with little visual differences.
5. Conclusion
In this paper, we proposed the method that controls texture resolutions based on their features. By allocating low resolutions to visually unimportant textures, we reduce the data size to load for rendering without much degradation of quality.
References
Haala N, Brenner C, Anders K: 3D urban GIS from laser altimeter and 2D map data. Proceedings of the ISPRS Commission III Symposium on Object Recognition and Scene Classification from Multispectral and Multisensor Pixels, July 1998, Columbus, Ohio, USA 339-346.
Haala N, Peter M, Kremer J, Hunter G: Mobile LiDAR mapping for 3D point cloud collection in urban areas: a performance test. Proceedings of the 21st International Archives of the Photogrammetry, Remote Sensing and Spatial Information Sciences (ISPRS '08), July 2008, Beijing, China 37, part B5, Commission 5: 1119ff.
Cornelis N, Cornelis K, Van Gool L: Fast compact city modeling for navigation pre-visualization. Proceedings of the IEEE Computer Society Conference on Computer Vision and Pattern Recognition (CVPR '06), June 2006, New York, NY, USA 2: 1339-1344.
Pollefeys M, Nistér D, Frahm J-M, et al.: Detailed real-time urban 3D reconstruction from video. International Journal of Computer Vision 2008,78(2-3):143-167. 10.1007/s11263-007-0086-4
Hoppe H: Progressive meshes. Proceedings of the 23rd Annual Conference on Computer Graphics and Interactive Techniques (SIGGRAPH '96), August 1996, New Orleans, La, USA 99-108.
Hoppe H: View-dependent refinement of progressive meshes. Proceedings of the 24th Annual Conference on Computer Graphics and Interactive Techniques (SIGGRAPH '97), August 1997, Los Angeles, Calif, USA 189-198.
Luebke D, Reddy M, Cohen JD, Varshney A, Watson B, Huebner R: Level of Detail for 3D Graphics. Morgan Kaufmann, San Francisco, Calif, USA; 2003.
Pajarola R: Large scale terrain visualization using the restricted quadtree triangulation. Proceedings of the IEEE Visualization Conference (Vis '98), October 1998, Research Triangle Park, NC, USA 19-26.
Losasso F, Hoppe H: Geometry clipmaps: terrain rendering using nested regular grids. Proceedings of the 31st International Conference on Computer Graphics and Interactive Techniques (SIGGRAPH '04), August 2004, Los Angeles, Calif, USA 769-776.
Hoppe H: Smooth view-dependent level-of-detail control and its application to terrain rendering. Proceedings of the IEEE Visualization Conference (Vis '98), October 1998, Research Triangle Park, NC, USA 35-42.
Cignoni P, Ganovelli F, Gobbetti E, Marton F, Ponchio F, Scopigno R: BDAM—batched dynamic adaptive meshes for high performance terrain visualization. Computer Graphics Forum 2003,22(3):505-514. 10.1111/1467-8659.00698
Cignoni P, Ganovelli F, Gobbetti E, Marton F, Ponchio F, Scopigno R: Interactive out-of-core visualization of very large landscapes on commodity graphics platform. Proceedings of the 2nd International Conference on Virtual Storytelling (ICVS '03), November 2003, Toulouse, France 21-29.
Döllner J, Buchholz H: Continuous level-of-detail modeling of buildings in 3D city models. Proceedings of the 13th ACM International Workshop on Geographic Information Systems (GIS '05), November 2005, Bremen, Germany 173-181.
Hu J, You S, Neumann U: Approaches to large-scale urban modeling. IEEE Computer Graphics and Applications 2003,23(6):62-69. 10.1109/MCG.2003.1242383
Takase Y, Yano K, Nakaya T, et al.: Visualization of historical city Kyoto by applying VR and web3D-GIS technologies. Proceedings of the 7th International Symposium on Virtual Reality, Archaeology and Cultural Heritage (VAST '06), October-November 2006, Nicosia, Cyprus
Wang H, Wexler Y, Ofek E, Hoppe H: Factoring repeated content within and among images. ACM Transactions on Graphics 2008,27(3):1-10.
Foley JD, van Dam A, Feiner SK, Hughes JF: Computer Graphics: Principles and Practice. Addison-Wesley, Reading, Mass, USA; 1995.
Inatsuka H, Uchino M, Okuda M: Level of detail control for texture on 3D maps. Proceedings of 11th International Conference on Parallel and Distributed Systems Workshops (ICPADS '05), July 2005, Fukuoka, Japan 2: 206-209.
Wandell BA: Foundations of Vision. Sinauer Associates, Sunderland, Mass, USA; 1995.
Long F, Zhang HJ, Feng DD: Fundamentals of content-based image retrieval. In Multimedia Information Retrieval and Management. Edited by: Feng D, Siu W, Zhang H. Springer, Berlin, Germany; 2003:1-26.
Flickner M, Sawhney H, Niblack W, et al.: Query by image and video content: the QBIC system. Computer 1995,28(9):23-32. 10.1109/2.410146
Perona P, Malik J: Scale-space and edge detection using anisotropic diffusion. IEEE Transactions on Pattern Analysis and Machine Intelligence 1990,12(7):629-639. 10.1109/34.56205
Pass G, Zabih R, Miller J: Comparing images using color coherence vectors. Proceedings of the 4th ACM International Multimedia Conference, November 1996, Boston, Mass, USA 65-73.
Zhang R, Zhang ZM: A clustering based approach to efficient image retrieval. Proceedings of the 14th International Conference on Tools with Artificial Intelligence (ICTAI '02), November 2002, Washington, DC, USA 339-346.
Goodrum AA: Image information retrieval: an overview of current research. Informing Science 2000,3(2):63-67.
Daly S: The visible difference predictor: an algorithm for the assessment of image fidelity. In Digital Image and Human Vision. Edited by: Watson AB. MIT Press, Cambridge, Mass, USA; 1993:179-206.
Acknowledgments
The authors are grateful for the support of a Grant-in-Aid for Young Sciences (#14750305) of Japan Society for the Promotion of Science, fund from MEXT via Kitakyushu innovative cluster project, and Kitakyushu IT Open Laboratory.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License ( https://creativecommons.org/licenses/by/2.0 ), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Inatsuka, H., Uchino, M., Ueno, S. et al. Texture Classification for 3D Urban Map. J Image Video Proc 2009, 432853 (2009). https://doi.org/10.1155/2009/432853
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1155/2009/432853



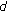 between the RV and the surface where the textures are mapped.
between the RV and the surface where the textures are mapped. of the texture in the 3D map.
of the texture in the 3D map.