- Research
- Open access
- Published:
Handling missing weak classifiers in boosted cascade: application to multiview and occluded face detection
EURASIP Journal on Image and Video Processing volume 2013, Article number: 55 (2013)
Abstract
We propose a generic framework to handle missing weak classifiers at testing stage in a boosted cascade. The main contribution is a probabilistic formulation of the cascade structure that considers the uncertainty introduced by missing weak classifiers. This new formulation involves two problems: (1) the approximation of posterior probabilities on each level and (2) the computation of thresholds on these probabilities to make a decision. Both problems are studied, and several solutions are proposed and evaluated. The method is then applied to two popular computer vision applications: detecting occluded faces and detecting faces in a pose different than the one learned. Experimental results are provided using conventional databases to evaluate the proposed strategies related to basic ones.
1 Introduction
Boosted cascade is a popular technique in the field of object detection. Boosting algorithms are learning algorithms that combine weak classifiers to produce a strong classifier. A weak classifier is a classifier that is slightly better than random to detect objects. A strong classifier is a classifier which is supposed to have high detection performance. When a candidate area is to be processed, each weak classifier is applied to a part of this area (see Figure 1a). In many computer vision detection applications, the algorithm has to handle partial observations, i.e., the object is partially occluded (see Figure 1b) or has to be detected in a pose different than the one learned (see Figure 1c). In such situations, weak classifiers that are in charge of classifying occluded areas tend to corrupt the final decision, i.e., the candidate area will often be classified as a non-object. Existing solutions consist in defining a set of finite occlusion configurations (or a set of pose configurations) and train multiple boosted cascades, one per configuration (see [1] for an example of multiview face detection). In the proposed solution, multiple training is avoided (only one classifier is used) and occluded weak classifiers are considered as missing data. A weak classifier is occluded when the data window of the weak classifier has hit an occluded part of the face.
Subwindows of weak classifier on an upright face, an occluded face, and a turned face. (a) An example of learned weak classifiers. Each one is in charge of classifying a subwindow. In (b), the face is occluded, and the subwindow of h 1 and h 3, filled in red, might be classified as non-face. Similarly, the face in (c) is turned 45°, and all subwindows might be classified as non-face.
Missing data in classification can be divided into two subproblems: (1) missing data at training stage and (2) missing data at testing stage. In this paper, we assume that missing data only occur at testing stage and that training is done with complete data. A recent study on missing data at testing stage can be found in [2] where Saar-Tsechansky and Provost evaluate different methods to handle missing data at testing stage. They compare two kinds of approach: reduced models and predictive value imputation. Their study does not focus on boosted cascades; the solution we propose in this paper is, to our knowledge, the first algorithm that handles missing data in a boosted cascade without modifying the initial training. Most existing solutions are based on learning algorithms that are designed to be robust to missing data. For example, Smeraldi et al. [3] used a modified version of adaptive boosting (AdaBoost) where weak classifiers can abstain when a feature is missing. Another algorithm was proposed by Globerson and Roweis [4] which is built to be robust to feature deletion. In the same way, Dekel and Shamir [5] improved this idea with an algorithm robust to feature deletion and feature corruption. Chen et al. proposed [6] a solution to detect occluded faces using only one upright face classifier, but they lost the cascade structure resulting in a high detection time.
Here we propose a generic solution to the problem of occluded object detection where occluded weak classifiers are considered as unavailable. Unavailable weak classifiers are seen as missing data, and this fact is incorporated in the cascade structure. We evaluate the proposed method for two different applications: (1) detecting occluded faces and (2) detecting faces in a pose different than the one learned. For each application, we explain how weak classifiers can be considered as available or not. Our method differs from former studies [1, 7] in two aspects: the proposed solution does not need the training of multiple classifiers, and, as opposed to existing methods where classifiers are designed to detect objects in a specific pose or with specific occlusions, the proposed solution relies on only one classifier that can adapt to specific poses or occlusions.
Section 2 presents the principle of boosted cascade. A new algorithm that handles missing weak classifiers in a boosted cascade is then detailed in Section 3. Application to occluded faces is presented in Section 4, followed by application to multiview face detection in Section 5. The proposed method is then evaluated in Section 6.
2 Boosted cascade overview
This section presents the principle of boosted cascade. The boosting algorithm was introduced by Schapire [8], and many extensions have been proposed. The main idea is to combine the performance of many weak classifiers to produce a powerful strong classifier. The goal is then to perform binary classification. In this paper, we focus on real boosting algorithms (e.g., Real AdaBoost, LogitBoost, or Gentle AdaBoost) which means that weak classifiers are real-valued functions.
Let be a training set where x i are training examples and y i ∈{-1,1} are their corresponding labels (1 is for the object class, also called positive class). Given this set, a real boosting algorithm iteratively finds T weak classifiers h t to form a strong classifier where x is a sample to be classified. Moreover, sign(h t (x)) gives the label of x predicted by h t , and the value |h t (x)| represents the confidence of the prediction. Each training example x i is an image R i of the object or non-object, and each weak classifier h t is learned on a set of subwindows which correspond to discriminative areas in all images (see Figure 1a for an example of such subwindows).
To speed up classification, Viola and Jones [9] proposed a cascade structure where several strong classifiers are associated into successive levels. The idea is that the first strong classifiers reject most of the negative examples, while the last strong classifiers try to discriminate positive examples from hard negative examples. In such cascades, strong classifiers are slightly changed into where α
j
are thresholds that are fixed during training (without cascade, α
j
=0). The training of a boosted cascade requires five elements: (1) the value f
max, the maximum acceptable false-positive rate per level; (2) the value d
min, the minimum acceptable detection rate per level; (3) the value F, the overall false-positive rate to be achieved, (4) a set of positive images; and (5) a set  of background images that will be used to generate interesting negative examples during training. The training of the level j consists of two steps: (1) applying the current cascaded detector (level 1 to j-1) on
of background images that will be used to generate interesting negative examples during training. The training of the level j consists of two steps: (1) applying the current cascaded detector (level 1 to j-1) on  to generate false-positives and create a set of negative examples and (2) using and to train the strong classifier sign(H
j
-α
j
). This one is designed so that a detection rate of at least d
min and a false-positive rate of at most f
max are achieved. Both parameters d
min and f
max are fixed by the user. These two steps are repeated until the constraint defined by F is satisfied. In this paper, we consider that the training stage is already done: the cascade of strong classifiers is available. The following section presents a generic framework to use this cascade when some weak classifiers h
jt
are missing at testing stage.
to generate false-positives and create a set of negative examples and (2) using and to train the strong classifier sign(H
j
-α
j
). This one is designed so that a detection rate of at least d
min and a false-positive rate of at most f
max are achieved. Both parameters d
min and f
max are fixed by the user. These two steps are repeated until the constraint defined by F is satisfied. In this paper, we consider that the training stage is already done: the cascade of strong classifiers is available. The following section presents a generic framework to use this cascade when some weak classifiers h
jt
are missing at testing stage.
3 Handling missing weak classifiers
This section presents the problem of missing weak classifiers in a boosted cascade, and solutions to this problem are then detailed. To explain our motivation, suppose we want to detect a face occluded by a scarf. In such a situation, all subwindows located on the lower part of the face will overlap the scarf, and thus all associated weak classifiers will tend to classify these subwindows as non-face. On the other hand, subwindows on the upper part of the face are likely to be classified as face. This is why we propose to consider weak classifiers corresponding to features on the lower part of the face as unavailable. Weak classifiers on the upper part of the face remain available. An example with three weak classifiers is given in Figure 2. In this section, it will be assumed that some weak classifiers are available and some are unavailable. We do not focus on why a weak classifier is available or not. These details will be given in Sections 4 and 5 which are dedicated to occluded face detection and to multiview face detection.
Example of a situation where some weak classifiers are missing. The face is occluded by a scarf. Rather than using all weak classifiers, we propose to use only the weak classifiers that should classify the upper part of the face (in green in the figure). The others, in red, are considered as unavailable.
3.1 Naive approach
Suppose that we want to classify a sample x with a strong classifier sign(H-α) where H is made up of a set of weak classifiers . Suppose also that only p<T weak classifiers are available, given by . The set of unavailable weak classifiers is defined as where q=T-p. In such a situation, the easiest strategy to classify x consists in setting all unavailable weak classifiers to zero, i.e., . If we note , the strong classifier becomes sign(H a-α). By applying this principle to all cascade levels, the set of strong classifiers becomes . To sum up, the naive approach consists in setting all unavailable weak classifiers to zero and keeping all cascade thresholds unchanged. This approach will be used as our baseline in the experiments section and will be referred to as 'naive approach’.
3.2 Probabilistic formulation of a boosted cascade
In a real boosting algorithm, the predicted label y∈{-1,1} of a sample x can be seen as a discrete random variable and H(x) can be interpreted as the probability of y being an object given the example x (also called the posterior probability) using the following sigmoid function [10]:
Thus, each cascade level computes P(y j =1|x) where y j is the predicted label of the level j. If a sample x reaches the level j, it means that it has passed all previous levels and is a candidate for an object. This is why we have . When weak classifiers are missing, uncertainty is introduced on each predicted label y j . This uncertainty is not considered in the probability as labels are supposed to be positive. This is why we propose to compute on level j. Thus, the predicted label on level j will also depend on predicted labels of level 1 to j-1. In the rest of the paper, the event will be noted y 1:j =1 to simplify the notation. To compute P(y 1:j =1|x), the following rule is used:
This rule gives:
By applying this rule recursively, we get:
This probabilistic formulation is very close to the one of Lefakis and Fleuret in [11]. Our motivation remains different because they proposed a new learning algorithm based on a probabilistic cascade formulation. In our case, we use a probabilistic formulation to handle the fact that some weak classifiers are missing at testing stage.
In a conventional cascade formulation, each level j applies a strong classifier H j to x and compares H j (x) with a threshold α j . With the probabilistic formulation, all thresholds α j disappear and new thresholds β j are introduced. Indeed, we have P(y j =1|x)≤1, and so:
Equation 6 shows that if P(y 1:j =1|x) is lower than a value β j , the cascade process should stop because will be even smaller. In the proposed framework, a strong classifier is defined as sign(P(y 1:j =1|x)-β j ). The complete modified boosted cascade is then defined by the set of strong classifiers . In the following, we refer to this modified cascade as boosted McCascade for boosted cascade with missing classifiers. Figure 3 sums up the differences between a cascade structure and a McCascade structure. Section 3.4 explains how values are computed, and the following section focuses on the estimation of P(y j =1|x).
Differences between a cascade and a McCascade for the classification of a sample x. In a cascade, all weak classifiers are used. At level j, H j (x) is computed and is compared to the threshold τ j . An occluded face is most of the time rejected because occluded subwindows corrupt the decision on each level. In a McCascade, only a subset of weak classifiers is used. In the figure, only weak classifiers in charge of classifying the upper part of the face are used. At level j, P(y 1:j =1|x) is computed and is compared to the threshold β j . An occluded face is most of the time detected. In contrast to the decision at level j of a cascade, the decision at level j of a McCascade incorporates the decision of previous levels.
3.3 Posterior probability estimation
When weak classifiers are missing, the probability P(y=1|x) can no longer be computed and an approximation must be used. We propose three different approximation strategies to do this:
-
The simplest strategy to estimate P(y=1|x) is to compute a probability based on available weak classifiers. Thus, we define P boost(y=1|x) as:
(7) -
A second strategy, noted P knn(y=1|x), tries to benefit from the initial training. Indeed, each training example x i provides a set of weak classifier values and an associated label y i . All these weak classifier values form a set , and the subset of available weak classifiers form where . The resulting set is used as a training set to approximate P(y=1|x) with the help of the k-nearest neighbor (k-nn) algorithm. Given a sample x, its associated available weak classifier scores are first computed. Then, the k-nn algorithm searches the k nearest neighbors of the point in the space . Considering the labels of the k nearest neighbors, the probability P knn(y=1|x) is computed as:
(8) -
where 1 lpred=1 if the predicate (pred) is true and 1 lpred=0 otherwise. Figure 4 illustrates the computation of P knn(y=1|x) when two weak classifiers are available.
-
An additional strategy, noted P comb(y=1|x), consists in combining the two previous methods as the simplest way:
(9)
Computation of P knn ( y =1|x) . Two weak classifiers are available: and . Applying these weak classifiers on a training database gives the set of points (the red circles are positive points and the blue squares are negative points). Given an unknown sample x, and are computed and the k nearest neighbors of are searched in . In the figure, k=3, and the nearest neighbors are two positive points and one negative point which leads to P knn(y=1|x)=2/3.
3.4 Boosted McCascade threshold estimation
Before a McCascade can be used to classify a sample x, the threshold must be estimated. The threshold estimation can be seen as the training stage of a McCascade. This is achieved through an iterative procedure which uses sets and  from the initial training stage. This procedure is described in Algorithm 1. At iteration j, the threshold β
j
of the level j is computed using the following scheme: all probabilities are first computed. Then, the set of probabilities is sorted and β
j
is chosen among the set of finite values . The function find_optimal_threshold (see line Algorithm 2) finds the threshold that minimizes a cost function defined on false-positive and true-positive rates. Contrary to the initial cascade where each level ensures reaching a true-positive rate of at least d
min with a false-positive rate less than f
max, the McCascade cannot guarantee the same performance. The cost function’s goal is to ensure that each threshold found provides a performance close to the initial cascade performance. Three cost functions are proposed:
from the initial training stage. This procedure is described in Algorithm 1. At iteration j, the threshold β
j
of the level j is computed using the following scheme: all probabilities are first computed. Then, the set of probabilities is sorted and β
j
is chosen among the set of finite values . The function find_optimal_threshold (see line Algorithm 2) finds the threshold that minimizes a cost function defined on false-positive and true-positive rates. Contrary to the initial cascade where each level ensures reaching a true-positive rate of at least d
min with a false-positive rate less than f
max, the McCascade cannot guarantee the same performance. The cost function’s goal is to ensure that each threshold found provides a performance close to the initial cascade performance. Three cost functions are proposed:
-
FP_cost is defined on the false-positive rate f β associated to a threshold β:
(10) -
The false-positive rate f β is computed on the training examples. Using this function means that the threshold found provides a false-positive rate which is as close as possible to f max (it remains greater or equal to f max).
-
TP_cost is defined on the true-positive rate d β associated to a threshold β:
(11) -
The true-positive rate d β is computed on the training examples. The threshold computed with this function will ensure a true-positive rate close to d min (it remains lower or equal to d min).
-
FP_TP_cost is defined on both false-positive and true-positive rates:
(12) -
This last cost function is a compromise between a false-positive rate of f max and a true-positive rate of d min.
A detailed version of find_optimal_threshold with the cost function FP_TP_cost is given in Algorithm 2. Once all the thresholds are estimated, the McCascade can be used to classify any unknown sample x.
Algorithm 1: McCascade threshold estimation

Algorithm 2: find_optimal_threshold

3.5 Cascade and McCascade training time
When a McCascade is created, the threshold must be computed. This step can be seen as the training stage of a McCascade. Compared to the training stage of a cascade, a McCascade needs fewer time to be trained. The training time of a cascade depends on a lot of parameters: number of training samples, number of levels, implementation (C++/MATLAB), …Rather than giving precise training times to compare a cascade and a McCascade, rough estimates are given here to emphasize the fact that a McCascade is faster to train than a cascade.
The training stage of a cascade can be split into three steps:
-
1.
Gather training data. Training data are made up of the positive images and of the background images. This step can last a few seconds if a public database exists. It can also last a few days if images must be manually gathered.
-
2.
Generate false-positives. At the beginning of each level, the negative samples are generated by applying the current classifier to the set of the background images. This step can last a few seconds to a few minutes.
-
3.
Train a cascade level. At each boosting iteration, several weak classifiers are learned (one for each subwindow), and the best one is kept. The number of iteration depends on the classification performance that must be reached. This step can last a few minutes to a few hours.
The training stage of a McCascade can be split into two steps:
-
1.
Generate false-positives. At the beginning of each level, the negative samples are generated by applying the current classifier to the set of the background images. This step can last a few seconds to a few minutes.
-
2.
Fix the level threshold. A probability is computed for each training example, and the threshold is computed according to these probabilities. This step can last a few milliseconds to a few seconds.
An object detector trained with a cascade is designed to detect the object in a specific pose or with specific occlusion. When the object has to be detected in a new pose or with new occlusion, a new object detector has to be designed. Using a cascade means that the three steps must be done again. On the opposite, using a McCascade just requires two steps that are not so time consuming. This is illustrated in Figure 5.
Differences between a cascade and a McCascade when several object detectors must be created. A rough estimate of the execution time is given for each step of the training process. (a) A new cascade must be trained for each new object detector. Each new training can last several hours to several days. (b) A new object detector can be trained using a McCascade. Each training just lasts several minutes.
4 Application to occluded face detection
Occlusions can greatly change the appearance of a face, and an upright face detector will easily fail to detect such faces. A cascaded detector that can deal with occlusions has already been proposed by Lin et al. [7]. Their solution relies on the training of nine cascaded detectors (one main cascade + eight occlusion cascades) that are then combined. This solution exhibits good performance at the cost of a prohibitive training time. On the other hand, Chan et al. [6] also proposed a detector to handle occlusion with only one training. They first train a boosted cascade and then combine all the weak classifiers learned to obtain a detector robust to occlusions. The problem is that the cascade structure is lost, resulting in an extensive execution time. Our solution relies on the use of an upright face detector  and the definition of several occlusion configurations where each occlusion configuration is associated with a McCascade. Each occlusion configuration is associated with a set of occluded weak classifiers from all the weak classifiers of the upright face detector. Based on this set, a McCascade that uses non-occluded weak classifiers can be built. Each McCascade created is called an occlusion cascade. Hence, we build several occlusion cascades which are then combined with the principle of cascading with evidence explained later.
and the definition of several occlusion configurations where each occlusion configuration is associated with a McCascade. Each occlusion configuration is associated with a set of occluded weak classifiers from all the weak classifiers of the upright face detector. Based on this set, a McCascade that uses non-occluded weak classifiers can be built. Each McCascade created is called an occlusion cascade. Hence, we build several occlusion cascades which are then combined with the principle of cascading with evidence explained later.
4.1 Occlusion cascade creation
Several occlusion cascades are created. Each one is in charge of a given occlusion type. To limit complexity, the case of two occlusion types is presented: bottom occlusion (called type  in Figure 6a) and top occlusion (called type
in Figure 6a) and top occlusion (called type  in Figure 6b). In occlusion
in Figure 6b). In occlusion  , the lower third of the face is considered as occluded. In occlusion
, the lower third of the face is considered as occluded. In occlusion  , the upper third of the face is considered as occluded.
, the upper third of the face is considered as occluded.
Let be the occluded area with , the set of occlusion configurations. Let be the region covered by the subwindow associated with the weak classifier h
jt
(see Figure 7). For each occlusion type  , the set of available weak classifiers must be defined to build the associated occlusion cascade. A weak classifier h
jt
is available for occlusion
, the set of available weak classifiers must be defined to build the associated occlusion cascade. A weak classifier h
jt
is available for occlusion  if the area does not intersect . In other words, the associated subwindow is considered as occluded for the occlusion
if the area does not intersect . In other words, the associated subwindow is considered as occluded for the occlusion  if the area intersects . For , two sets and of available weak classifiers are defined:
if the area intersects . For , two sets and of available weak classifiers are defined:
Based on these two sets, two McCascades and can be created. only uses weak classifiers defined in . In the same way, only uses weak classifiers defined in . Finally, thresholds β j of both McCascades are fixed with the help of Algorithm 1.
4.2 Cascading with evidence
To combine the main cascade  and the two occlusion cascades and , the principle of cascading with evidence proposed by Lin et al. [7] is used. When a sample x must be tested, it first goes through the main cascade. At level j of this cascade, in addition to applying the strong classifier H
j
, an additional feature vector ε
j
(x) is also computed:
and the two occlusion cascades and , the principle of cascading with evidence proposed by Lin et al. [7] is used. When a sample x must be tested, it first goes through the main cascade. At level j of this cascade, in addition to applying the strong classifier H
j
, an additional feature vector ε
j
(x) is also computed:
where
The vector ε j (x) is called the evidence of x at level j.
Equation 16 means that only involves weak classifiers over subwindows that do not intersect with . With the evidence vector presented in Equation 15, weak classifiers can now be defined as available or not depending on the occlusion encountered. Indeed, let x be an occluded face example of type  and suppose that the main cascade
and suppose that the main cascade  rejects it at level j because H
j
(x)<α
j
. Before rejecting it, we check the evidence vector of x. In particular, the majority of should be positive, indicating that x is an occluded face of type
rejects it at level j because H
j
(x)<α
j
. Before rejecting it, we check the evidence vector of x. In particular, the majority of should be positive, indicating that x is an occluded face of type  . Based on this fact, weak classifiers that can handle occlusion
. Based on this fact, weak classifiers that can handle occlusion  (i.e., h
jt
verifying ) are defined as available, and x continues the classification process with the McCascade defined on available weak classifiers. Generally speaking, if a sample is occluded of type
(i.e., h
jt
verifying ) are defined as available, and x continues the classification process with the McCascade defined on available weak classifiers. Generally speaking, if a sample is occluded of type  and if this sample is rejected by the main cascade, this sample will be passed to the McCascade . Note that with this principle of cascading with evidence, there is no explicit occlusion detection.
and if this sample is rejected by the main cascade, this sample will be passed to the McCascade . Note that with this principle of cascading with evidence, there is no explicit occlusion detection.
Using  , , and with the principle of cascading with evidence, we can detect occluded faces following the testing procedure described in Algorithm 3 where represents the McCascade that can handle occlusion
, , and with the principle of cascading with evidence, we can detect occluded faces following the testing procedure described in Algorithm 3 where represents the McCascade that can handle occlusion  . The testing procedure is also illustrated in Figure 8. All the above explanations remain valid with other types of occlusions. Note that the number of occlusions that can be handled only depends on the weak classifiers learned during the initial training. For example, if all the weak classifiers learned are associated with subwindows located on the upper part of the face, it would be impossible to handle occlusions of type
. The testing procedure is also illustrated in Figure 8. All the above explanations remain valid with other types of occlusions. Note that the number of occlusions that can be handled only depends on the weak classifiers learned during the initial training. For example, if all the weak classifiers learned are associated with subwindows located on the upper part of the face, it would be impossible to handle occlusions of type  .
.
Algorithm 3: Detecting occluded objects with several McCascades combined with cascading with evidence

5 Application to multiview face detection
In this section, we are interested in the detection of faces with rotation-off-plane (ROP) angles. Examples of such faces are exposed in Figure 9. Upright face detectors are robust to slight ROP angles (they can usually detect faces turned up to ±20°). Detection of faces with bigger ROP angles need specific solutions. Most of the existing methods adopt the view-based approach: several classifiers are trained and then combined to get a multiview face detector [1, 12, 13]. In such an approach, each classifier is trained to detect faces with ROP angles in a given range which means that multiple training is necessary. To avoid these multiple trainings, we propose to create a classifier that can detect faces in a pose different than the one learned.
5.1 Detecting faces with ROP angle
Our solution is composed of an upright face detector that we modify to be able to detect faces with a given ROP angle. To incorporate the fact that faces may have out-of-plane rotations, we propose to adjust all the subwindow positions. Our idea is illustrated in Figure 10c. Figure 10a shows three interesting subwindows used to detect upright faces. In Figure 10b, we represent the same subwindows on a face turned 45°. The three subwindows are not anymore informative. To alleviate this problem, we can modify the position of the three subwindows (see Figure 10c). Note that the position modification can lead to a modification of the subwindow size (see the yellow subwindow) or the disappearance of some subwindows (see the red subwindow).
Detecting turned faces with an upright face detector. (a) An example of three discriminative subwindows of an upright face detector. h 1, h 2, and h 3 are the associated weak classifiers. (b) The face is turned 45°, and all subwindows could be classified as non-face. To alleviate the pose problem, we propose a three-dimensional geometric transformation to adjust all subwindow positions (see (c)). Note that the weak classifier h 3 becomes unavailable.
To modify a subwindow position, we propose to use the three-dimensional (3D) transformation which exists between an upright face and the same face in another pose. In our case, these transformations are the set of rotations around the x-axis and y-axis. To simulate a rotation, we need a 3D face model. Building an accurate 3D face model requires at least two images per face. As our intention is to avoid gathering images other than upright faces, we decide to represent a face with the simplest model: an ellipsoid. The idea is then to place each subwindow on the ellipsoid, turn the ellipsoid, and finally get back all the new subwindows positions. Let us consider a point of an image of size w×w (the same size as training images) whose coordinates are expressed in the image coordinate system . The process to compute the position of this point after a rotation defined by an angle of θ x around the x-axis and an angle of θ y around the y-axis is made up of the following three steps:
-
1.
We associate a point to the point . is the 3D point with the same x-coordinate and y-coordinate as that belongs to the ellipsoid. We just have to compute the z-coordinate w 1 with the help of the ellipsoid equation expressed in (see Figure 11a):
(17)
where u o =w/2, v o =w/2, and w o =0 and a, b, and c are the ellipsoid’s parameters.
-
2.
We express in the coordinate system whose origin is the ellipsoid center. This gives us the point:
(18)
and then, we have to which we apply the rotation to obtain the point (see Figure 11b):
where R y (θ y ) and R x (θ x ) are rotation matrices around the y-axis and x-axis.
-
3.
Finally, we express in to get the point (see Figure 11c):
(20)
We have . The point we are looking for is .
Rotation process of a point using an ellipsoid. (a) The image point is associated with the point on the ellipsoid using the ellipsoid equation. (b) is expressed in the ellipsoid coordinate system which gives the point . The rotated point is computed using rotation matrices. (c) is expressed in the image coordinate system which gives the point and the image point .
To know the position of a subwindow r jt after a rotation, we apply the above process to the top left corner and to the bottom right corner of r jt . The problem is that some subwindows can disappear (as shown in Figure 10c with the subwindow of h 3 in red). If a subwindow r jt disappears, then the associated weak classifier h jt becomes unavailable. By applying this rule to all the subwindows, the set of available weak classifiers can be defined and an associated McCascade can be built. Hence, creating a classifier that can detect non-upright faces calls for three steps:
-
1.
Modifying the position of all subwindows using an ellipsoid model,
-
2.
Defining the set of available weak classifiers by checking that their associated subwindows do not disappear after rotation, and
-
3.
Creating the McCascade using available weak classifiers.
5.2 A multiview system
The solution presented in the last section aims to detect faces with a given ROP angle θ y . When faces with a ROP angle in a range are to be detected, one solution is to combine several detectors. Each one is specialized in detecting faces with a given ROP angle θ y . In practice, it is generally assumed that each detector can detect faces in the range [θ y -15,θ y +15]. For example, if the total range is [-45,+45], three detectors must be used: an upright face detector H0, a detector of faces turned +30°H+30, and a detector of faces turned -30°H-30. Detectors H+30 and H-30 are created by modifying all subwindow positions by H0. To combine the three detectors, the solution proposed by Huang et al. [14] is applied. It is illustrated in Figure 12. To speed up the classification process, a pose estimator is used. For an input example x, this estimation consists in applying the first three levels of every detector to x. Then, the classification process continues with the detector that accepts x with the highest classification score. The pose estimation function is defined by:
Note that the system used to combine the three detectors can be extended to get a face detector robust to pose and to occlusion. Indeed, using this system, several occlusion cascades (presented in Section 4.1) and several pose-specific detectors (presented in Section 5.1) can be combined.
6 Experiments
This section presents the experiments achieved in order to (1) evaluate the performances of McCascade compared to the naive approach and (2) evaluate the McCascade algorithm for two concrete applications: occluded face detection and multiview face detection. In these experiments, upright face detectors are similar to the system of Tuzel et al. [15]: covariance matrices are used as features [16], and the learning algorithm is a cascade of LogitBoost [10]. Weak classifiers are linear functions that are learned from a set of feature vectors. A feature vector is derived from a covariance matrix by taking its upper triangular part. The only difference with the system [15] is that we assume that a feature vector lies on a vector space (in [15], a feature vector lies on a Riemannian manifold).
The first part of the experiments related to McCascade performance (Sections 6.2 and 6.3) are done with an upright face cascaded detector of three levels with 5, 10, and 25 weak classifiers, respectively. Positive examples come from the labeled upright faces in the wild database [17], and negative samples were generated from 1,310 images containing no face. A total of 4,000 positive examples and 8,000 negative examples are used to train each cascade level. The second part of the experiments related to applications (Sections 6.4, 6.5, and 6.6) are done with an upright face detector of nine levels. This detector is noted  . Each level was trained with 5,000 positive examples and 5,000 negative examples. Each level was designed so that a detection rate of at least d
min=0.998 and a false-positive rate of at most f
max=0.5 were achieved on training examples. The positive examples again come from the labeled upright faces in the wild database, and negative samples were generated from 2,500 images containing no face. The FLANN library [18] is used to perform nearest neighbor searches (used in P
knn and P
comb). The test database is the CMU frontal face test A which consists of 42 images showing 169 upright faces with varied background [19].
. Each level was trained with 5,000 positive examples and 5,000 negative examples. Each level was designed so that a detection rate of at least d
min=0.998 and a false-positive rate of at most f
max=0.5 were achieved on training examples. The positive examples again come from the labeled upright faces in the wild database, and negative samples were generated from 2,500 images containing no face. The FLANN library [18] is used to perform nearest neighbor searches (used in P
knn and P
comb). The test database is the CMU frontal face test A which consists of 42 images showing 169 upright faces with varied background [19].
In the first part of the experiments, receiver operator characteristic (ROC) curves are used to evaluate and compare performances, and all performances exhibited are raw, i.e., the post-processing step of merging multiple detections is not taken into account here. This means that the false-positive rate can be reduced with this post-processing step without modifying the true-positive rate. When multiple detections occur for the same person, only the one with the highest classification score is kept. The others are simply ignored. In the second part of the experiments, free ROC(FROC) curves are used, and multiple detections are merged. Contrary to the ROC curve which plots detection rate versus false acceptance rate, the FROC curve plots the detection rate versus the number of false-positives and is more suited to evaluate performances of an object detector in specific applications. Different experiments were conducted to evaluate the different aspects of our method. In Section 6.2, we test the three proposed cost functions TP_cost, FP_cost, and FP_TP_cost used in the computation of McCascade’s thresholds. Then, Section 6.3 deals with the evaluation of the different strategies used to estimate posterior probability: P boost, P knn, and P comb. After these two series of experiments, we apply our method to two specific applications: detecting faces occluded by a scarf or sunglasses (see Section 6.4) and detecting faces in a pose different than the one learned (see Section 6.5).
6.1 Good detection criterion
Building ROC or FROC curves requires computing true-positive rates and false-positive rates. A criterion must be defined to decide if a given detection is a true-positive or a false-positive. The criterion used in these experiments is defined in the overlap between the detection and the ground truth. It was proposed by Yao and Odobez [20]. The overlap is computed with the F measure F overlap:
ρ stands for the precision area and π for the recall area. GT is the ground truth area, and D is the detection area. The operator |R| is the number of pixels in the area R. A detection matches with ground truth if F overlap>0.5.
6.2 Evaluation of threshold estimation strategies
In this first part, we evaluate the influence of the cost function in threshold β j estimation when a given proportion of weak classifiers is missing. We chose to consider 50% and 60% of missing weak classifiers because these rates are realistic in occluded face detection. Given a missing weak classifier rate, we randomly create two sets of weak classifiers per level to be considered as unavailable. For example, consider the level 2 of the classifier which has ten weak classifiers. If 60% of the weak classifiers are missing, then 6 weak classifiers must be selected as unavailable. For each of the two sets of unavailable weak classifiers, we randomly select six weak classifiers to be considered as unavailable. These two sets could be {h 21, h 22, h 23, h 24, h 27, h 29} and {h 22, h 23, h 25, h 26, h 27, h 28}. Given the sets of the three levels, there are 2×2×2=8 possible configurations to test resulting in eight ROC curves. Means and standard deviations are then computed to produce the final ROC curve. For each configuration, thresholds are first computed and the resulting classifier is applied to the test database. This test process is repeated for each cost function associated to each posterior probability computation strategy: P boost, P knn, and P comb. For the last two strategies, we fix the number of neighbors k at 3. All the ROC curves are available in Figure 13. In all the curves, the cost function TP_cost produces a classifier that outperforms the other classifiers produced with FP_cost and FP_TP_cost.
Performance of classifiers produced with the three cost functions: TP_cost, FP_cost and FP_TP_cost. In (a, b, c), 50% of the weak classifiers are unavailable, while 60% of the weak classifiers are unavailable in (d, e, f). In (a) and (d), posterior probabilities are computed with P boost. In (b) and (e), P knn is used, and P comb is used in (c) and (f). The number of neighbors in P knn and P comb is fixed at 3.
ROC curves are useful in evaluating the overall performance of a classifier. When we train a classifier, this presents a given true-positive rate and a given false-positive rate which should be consistent with the application targeted. In face detection, we are interested in having a high true-positive rate and a low false-positive rate. This is why, in addition to ROC curves, we present the false-positive rate, noted FP, and the true-positive rate, noted TP, of classifiers produced by the three cost functions. Results for a missing rate of 50% can be found in Table 1, while results for 60% are available in Table 2. In these tables, we also print the mean number of levels evaluated per negative example, noted . This criterion reflects the impact of the cost function on the execution time of the classifier. Indeed, a high number of evaluated levels per negative example will bring a high execution time. In both tables, we print in italics the cost function that provides the most consistent performance. As expected, the use of cost functions FP_cost and FP_TP_cost involves low false-positive rates but also involves low true-positive rates (some of them lower than 10%), which means that these classifiers do not have a practical value. Furthermore, the impact on the mean number of evaluated levels is not very significant: we note an increase of about 7% between the cost function TP_cost and the two others. These experiments prompt us to keep the cost function TP_cost because FP_cost and FP_TP_cost tend to decrease the true-positive rate and the overall performance.
6.3 Performance of the posterior probability estimation
In this section, we evaluate the three strategies to estimate posterior probabilities proposed in Section 3.3: P boost, P knn, and P comb. The evaluation methodology is the same as the previous section (same cascaded detector, same test database, same missing rate). Here, the cost function used to compute thresholds is TP_cost. Five configurations are compared: (1) 'CascadeF’ is the initial cascade with the full set of weak classifiers (can be seen as an upper bound), (2) 'CascadeA’ is the naive approach presented in Section 3.1 where the initial cascade is only used with available weak classifiers, (3) 'McCascade + Pboost’ is a McCascade used with available weak classifiers where posterior probabilities are computed with P boost, (4) 'McCascade + Pknn’ is a McCascade used with available weak classifiers where posterior probabilities are computed with P knn, and (5) 'McCascade + Pcomb’ is a McCascade used with available weak classifiers where posterior probabilities are computed with P comb. When P knn and P comb are used, only the best results are plotted (k=7 for P knn and k=3 for P comb). The results can be found in Figure 14. In both cases, the McCascade structure improves the performance. The most interesting results are obtained when P knn and P comb are used. In that case, the true positive rate increases from 10 to 30% when 50% of weak classifiers are unavailable. When 60% of weak classifiers are unavailable, the improvement is even higher: from 20% to 60%. In both cases, the proposed method outperforms the naive approach. Moreover, McCascade is really more stable than the naive approach (see standard deviations in each curve) which ensures good performance in every case. Finally, the proposed method does not suffer from the additional 10% of unavailable weak classifiers. Even if P knn and P comb are close in terms of performance, we note that P knn is slightly better.
Comparison of different strategies to estimate posterior probability in a boosted McCascade. They are for different rates of missing weak classifiers. In (a), 50% of weak classifiers are missing, while in (b), 60% are missing. Each McCascade can be compared with the naive approach presented in Section 3.1 where the initial boosted cascade is used with available weak classifiers (noted CascadeA). In each curve, we also plot the performance of the boosted cascade when all weak classifiers are known (noted CascadeF) to show the effect of missing weak classifiers on initial performance (best view in color).
The influence of the number of neighbors in the McCascade coupled with the strategy P knn can be found in Figure 15. In both cases, k=7 gets the best performances, but k=3 should be preferred as it provides similar performance and lower computational cost. In all the following experiments, the McCascade is used with the P knn strategy and k=3.
An additional result is given in the Figure 16 where 30% of the weak classifiers are missing. Below this rate of 30%, the naive approach and the McCascade get close performances. However, when at least 30% of the weak classifiers are missing, using a McCascade becomes interesting. Indeed, it can be noted in Figure 16 that a McCascade with the strategy P knn increases the true-positive rate up to 30% compared to the naive approach.
6.4 Occluded face detection
In this section, we evaluate the performance of McCascade coupled with the principle of cascading with evidence in a specific application: detecting faces with top occlusions (like sunglasses) or bottom occlusions (like a scarf). We only consider these two types of occlusions for two reasons. The first is that we are working in a video surveillance context in which these two types of occlusions are often encountered. The second reason is that a public database with these two types of occlusion is available: the AR database.
6.4.1 Evaluation on the AR database
The AR database [21] is used first. In particular, we use the 765 images of faces occluded by a scarf and the 765 images of faces occluded by sunglasses. The classifier used here is the upright face detector of nine levels. Using this cascade , we build a McCascade that can handle bottom occlusion and a McCascade that can handle top occlusion. Also, a detector that associates
, we build a McCascade that can handle bottom occlusion and a McCascade that can handle top occlusion. Also, a detector that associates  , , and with the principle of cascading with evidence is created. This detector will be noted 'McCascades + evidence’ in the results. The McCascade has, on average, 42% unavailable weak classifiers per level. The McCascade has, on average, 46% unavailable weak classifiers per level.
, , and with the principle of cascading with evidence is created. This detector will be noted 'McCascades + evidence’ in the results. The McCascade has, on average, 42% unavailable weak classifiers per level. The McCascade has, on average, 46% unavailable weak classifiers per level.
Two scenarios are tested:
-
Scenario 1. We consider images of faces occluded by a scarf, and we then compare (1) the cascade
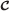 , (2) the McCascade , and (3) the detector McCascades + evidence.
, (2) the McCascade , and (3) the detector McCascades + evidence. -
Scenario 2. We consider images of faces occluded by sunglasses, and we then compare (1) the cascade
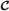 , 2) the McCascade , and (3) the detector McCascades + evidence.
, 2) the McCascade , and (3) the detector McCascades + evidence.
For all scenarios, FROC curves are computed. To create the FROC curve of a cascaded detector, several threshold values are tested for the last level which results in corresponding points of detection rate and number of false-positives. To get more points (points with a higher detection rate and a higher number of false-positives), the last level must be removed, and then different thresholds for the new last level are tested. This procedure continues until enough points are collected. When several cascades are associated (e.g., in the system '  + + + evidence’), creating a FROC curve is not straightforward because each cascade has its own thresholds. To alleviate this problem, we use the idea proposed by Viola and Jones in [22]. To create FROC curves from multiple cascades, thresholds are simultaneously modified in all cascades. In the same way, layers are simultaneously removed in all cascades.
+ + + evidence’), creating a FROC curve is not straightforward because each cascade has its own thresholds. To alleviate this problem, we use the idea proposed by Viola and Jones in [22]. To create FROC curves from multiple cascades, thresholds are simultaneously modified in all cascades. In the same way, layers are simultaneously removed in all cascades.
The FROC curve of scenario 1 is available in Figure 17. The McCascade (noted 'McCascade’) greatly improves the detection rate (up to 30%). The drawback of is that it is designed to detect faces with bottom occlusions. When the encountered occlusion is unknown (top or bottom), the detector McCascades + evidence can be used, and Figure 17 shows that its performances are close to the ones of .
The FROC curve of scenario 2 is available in Figure 18a. On faces occluded by sunglasses, the initial cascade and the proposed solutions (the detector and the detector McCascades + evidence) expose very poor results. The poor results in scenario 2 are due to a limitation in our solution: the fact that each weak classifier does not have the same performance. Several works on face detection noticed that learned weak classifiers often rely on the upper part of the face to make a decision because the eye area is very discriminative. When our upright face detector was trained, we noticed the same phenomenon: most of the weak classifiers are located on the upper part of the face, and they are more powerful than the weak classifiers located on the lower part of the face. This fact can be seen in Figure 18b which represents a performance map  of all the weak classifiers in the initial cascade. To build this map, we first initialize all values to zero. Then, for all the weak classifier h
jt
, we compute its classification rate CR
jt
(rate of well-classified positive and negative examples), and we update
of all the weak classifiers in the initial cascade. To build this map, we first initialize all values to zero. Then, for all the weak classifier h
jt
, we compute its classification rate CR
jt
(rate of well-classified positive and negative examples), and we update  with:
with:
Limitation of the proposed solution. (a) Comparison of the initial cascade  (noted Cascade), the McCascade (noted McCascade), and the association of
(noted Cascade), the McCascade (noted McCascade), and the association of  , , and with the principle of cascading with evidence (noted McCascades + evidence) on faces occluded by sunglasses. (b) Performance map of all the weak classifiers in the initial cascade. Note that most of the performance is located on the upper part of the face (best seen in color).
, , and with the principle of cascading with evidence (noted McCascades + evidence) on faces occluded by sunglasses. (b) Performance map of all the weak classifiers in the initial cascade. Note that most of the performance is located on the upper part of the face (best seen in color).
Finally, we normalize all the values between 0 and 1. Based on this map, we understand that our method fails on faces occluded by sunglasses because, in this scenario, we only use weak classifiers located on the lower part of the face which are too weak to ensure good performance.
In scenario 2, the existing solutions such as [7] will exhibit better results. Indeed, a specific classifier will be trained to detect faces with top occlusions. In scenario 1, it is interesting to compare our system with [7]. Rather than building the complete system described in [7], a specific classifier was trained to detect faces with bottom occlusion. This specific classifier is close to cascade , except that all the learned weak classifiers are located on the area that it is not occluded. This specific classifier is then compared with the McCascade . Results can be found in the Figure 19. Except with a very low number of false-positives, the specific classifier gets a higher detection rate (up to 10%).
, except that all the learned weak classifiers are located on the area that it is not occluded. This specific classifier is then compared with the McCascade . Results can be found in the Figure 19. Except with a very low number of false-positives, the specific classifier gets a higher detection rate (up to 10%).
6.4.2 Evaluation in real-life scenario
A test is also done in a real-life scenario. A camera is placed on a pole to film a group of 15 persons. Some of them have their face occluded by a scarf, coat, or hood. Examples of images from the sequence are available in Figure 20. There is a small angle (around 20°) between the optical axis of the camera and the ground to imitate conditions of a video surveillance context.
Three detectors are applied to this sequence:
-
Upright face detector
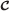 . It is noted 'FDcov’ in the results.
. It is noted 'FDcov’ in the results. -
Detector that associates
 ,, and with the principle of cascading with evidence. It is noted 'FDcov + occlusion’ in the results.
,, and with the principle of cascading with evidence. It is noted 'FDcov + occlusion’ in the results. -
Upright face detector of the OpenCV library (the file
-
haarcascade_frontalface_alt_tree.xml is used). This detector is the implementation of the solution of Lienhart et al. [23]. This classifier is a cascade of boosted classifiers. Haar features are used. It is noted 'FDhaar’ in the results.
The detector FDhaar just gives output detections. The classification score of each detection is not known. This detector is applied first on the sequence. Then, with the help of ground truth, the detection rate per person is computed. The number of false-positives nbFPhaar is also noted. The other two detectors are then applied to the sequence. The rejection thresholds of the two detectors are modified so that they obtain nbFPhaar false-positives. Then, the detection rate per person is computed. The results are available in Figure 21. The red line is the average detection rate of the detector FDhaar. The yellow line is the average detection rate of the detector FDcov, and the green line is the average detection rate of the detector FDcov + occlusion. The worst performances are obtained with FDhaar with 38% true-positive rate. FDcov gets a 47% true-positive rate. The best performances are achieved by FDcov + occlusion with a true positive rate of 75%. Moreover, we note that FDhaar does not detect persons 11, 12, and 14. They are detected by the other two classifiers. Detection examples of these persons are given in Figure 22.
Comparison of FD haar , FD cov , and FD cov + occlusion on a realistic sequence. Each number on the horizontal axis is associated to a person in the sequence. The vertical axis is the detection rate. The red line is the average detection rate of FDhaar. The yellow line is the average detection rate of FDcov and the green line is the average detection rate of FDcov + occlusion.
6.5 Multiview face detection
In this part of the experiments, the boosted McCascade algorithm has been applied to another specific application: detecting faces in different poses using an upright face detector. The FERET database [24] was used to evaluate the system. We test our method on faces turned 22.5°, 45° and 67.5°. For each angle, all the subwindow positions are first adjusted using the procedure described in Section 5.
6.5.1 Ellipsoid parameters
To modify the subwindow positions, parameters w, a, b, and c must be fixed. Parameter w corresponds to the size of the training images which is 24 in our case. To fix ellipsoid parameters a, b, and c, we do an exhaustive search and keep the parameters, giving the best results on validation sets from the FERET database. Two validation sets were created: one for the angle 22.5° and one for 45°. For each angle, we keep half of the images to fix the ellipsoid parameters. The other half is used to evaluate the complete system. For each parameter value (a i ,b i ,c i ), we apply the following methodology:
-
1.
Based on the upright face classifier, we create two classifiers and by adjusting all the subwindow positions using ellipsoid parameters (a i ,b i ,c i ). Subwindows that disappear are handled by the naive approach presented in Section 3.1, i.e., associated weak classifiers are simply ignored.
-
2.
is applied to the validation set of images of faces turned 22.5°, and the ROC curve is computed. Then, the area under ROC curve is computed which gives (auc is a criterion to compare ROC curves: the higher it is, the better the ROC curve). Using , we also get .
-
3.
Finally, the overall value is computed.
Parameters with the best value auc i were kept. We found that a=2.0∗w/2, b=w. and c=w/2 give the best results.
6.5.2 Modification of subwindow positions
Here, the use of an ellipsoid to modify subwindow positions is evaluated. Three detectors are built:
-
is a detector of faces that turned 22.5°,
-
is a detector of faces that turned 45°, and
-
is a detector of faces that turned 67.5°.
Each one is built from  by modifying subwindow positions. Subwindows that disappear are handled by the naive approach. These detectors are then applied to images from the FERET database. The results are available in Figures 23 and 24. In each curve, the upright face detector
by modifying subwindow positions. Subwindows that disappear are handled by the naive approach. These detectors are then applied to images from the FERET database. The results are available in Figures 23 and 24. In each curve, the upright face detector  is noted 'Cascade’. Detectors, and are noted 'MaCascade’ (for cascade with multiview adaptation). On faces turned 22.5°, the improvement is slight because the appearance of such faces is still close to the appearance of upright faces. The improvement is greater on faces turned 45°. Indeed, the detection rate increases from 30% to 40%. Finally, we see that the detection of faces turned 67.5° can be seen as a limitation of the proposed method. A detection rate increase (up to 60%) only occurs when the number of false-positives becomes high (>30). This limitation comes from the step of adjusting the subwindow positions:
is noted 'Cascade’. Detectors, and are noted 'MaCascade’ (for cascade with multiview adaptation). On faces turned 22.5°, the improvement is slight because the appearance of such faces is still close to the appearance of upright faces. The improvement is greater on faces turned 45°. Indeed, the detection rate increases from 30% to 40%. Finally, we see that the detection of faces turned 67.5° can be seen as a limitation of the proposed method. A detection rate increase (up to 60%) only occurs when the number of false-positives becomes high (>30). This limitation comes from the step of adjusting the subwindow positions:
Performances of different detectors on faces turned 22.5° in (a) and 45° in (b). The detector Cascade is the upright face detector. The detector MaCascade is built from the upright face detector and aims to detect turned faces. Subwindow positions are modified and unavailable weak classifiers are handled by the naive approach. The detector MaMcCascade is the same detector as MaCascade except that unavailable weak classifiers are handled with a McCascade. The detector MaMcCascade multiview is a multiview system that combines three MaMcCascades: one for the angle 22.5°, one for 45°, and one for 67.5°.
Performances of different detectors on faces turned 67.5° . The detector Cascade is the upright face detector. The detector MaCascade is built from the upright face detector and aims to detect turned faces. Subwindow positions are modified and unavailable weak classifiers are handled by the naive approach. The detector MaMcCascade is the same detector as MaCascade except that unavailable weak classifiers are handled with a McCascade. The detector MaMcCascade multiview is a multiview system that combines three MaMcCascades: one for the angle 22.5°, one for 45°, and one for 67.5°.
-
1.
The subwindow position modification should compensate the modified appearance of a turned face of an angle θ y . When the angle θ y increases, it becomes much more difficult to compensate the modified appearance as the modification becomes stronger and stronger.
-
2.
In Section 5, we explain that some subwindows can disappear due to rotation. In fact, the number of subwindows that disappear increases with the angle θ y . This loss impacts the initial performance.
6.5.3 Association with a McCascade
The three detectors of the previous section , , and have some unavailable weak classifiers:
-
has, on average, 18% unavailable weak classifiers per level.
-
has, on average, 27% unavailable weak classifiers per level.
-
has, on average, 44% unavailable weak classifiers per level.
Unlike using the naive approach to handle these unavailable weak classifiers, it could be interesting to modify the cascade structure into a McCascade. In this section, the structure of the three detectors is changed into a McCascade. The strategy P knn is used with k=3 neighbors, and thresholds β j are fixed using the cost function TP_cost. In Figures 23 and 24, these detectors are noted 'MaMcCascade’. On faces turned 22.5° and 45°, the improvement compared to the naive approach is slight (increase of the detection rate from 2% to 5%). The impact of using a McCascade is greater on faces turned 67.5°. Indeed, contrary to the naive approach, the McCascade allows for the detection rate to be improved with only a few false-positives. However, performances remain limited. For example, 55% of faces are detected with 12 false-positives, while this rate is 90% when faces are turned 22.5° and 45°.
Detecting faces turned 67.5° with the existing solutions such as [1, 12, 13] will exhibit better results. Indeed, a specific classifier will be train to detect faces turned 67.5°. When faces are turned 45°, it is interesting to compare the system MaMcCascade with a specific classifier. Thus, a specific classifier was trained using the same training parameters as the cascade  , except that the positive images were extracted from the FERET database. A total of 132 images of faces turned 45° were extracted to train the specific classifier (these images are not used during the testing stage). Results can be found in Figure 25 where we see that the specific classifier gets a higher detection rate (up to 10%).
, except that the positive images were extracted from the FERET database. A total of 132 images of faces turned 45° were extracted to train the specific classifier (these images are not used during the testing stage). Results can be found in Figure 25 where we see that the specific classifier gets a higher detection rate (up to 10%).
6.5.4 The multiview system
In the previous sections, the pose of faces was known. Here, a multiview system is evaluated. This system can detect faces with different ROP angles. The three detectors , , and are combined to get the multiview system following the principle of Section 5.2. Unavailable weak classifiers are handled with a McCascade. In Figures 23 and 24, this detector is noted 'MaMcCascade multiview’. It gets performances that are close to performances of specific detectors (noted MaMcCascade on each curve).
6.6 Computation time
In this section, we compare the execution time of the proposed method on the two applications. For the multiview application, we compare the initial upright face detector and the system MaMcCascade on faces turned 45°. The mean detection time per image, the minimum detection time, and the maximum detection time can be found in Table 3. For the occluded face detection application, we compare the initial upright face detector (noted Cascade) with the system of the initial cascade associated with a McCascade with the principle of cascading with evidence (noted McCascade + evidence) on faces occluded by a scarf. Table 4 contains detection times of the two systems. In both applications, classifiers were run five times and detection times were averaged. In both tables, we see that averaged detection time increases by about 25% when we use our solution.
7 Conclusions
We have presented a solution for handling missing weak classifiers in a boosted cascade. Our method relies on a probabilistic formulation of the cascade structure and on the computation of posterior probability on each level. To make a decision on each level, thresholds have been introduced and are fixed through an iterative procedure that minimizes a cost function. All aspects of the proposed solution have been tested. Moreover, the method has been successfully applied to two specific applications which involve occluded faces. During experiments on occluded faces and on turned faces, we also discuss limitations of the proposed solution which are due to performance differences between weak classifiers. On the other hand, the main advantage of the proposed method is that it only uses an existing face classifier; additional training is not needed to detect occluded faces or faces in another pose. Future work will focus on the method’s limitation on occluded faces. During experiments on occluded faces, we notice that the proposed solution can fail on some occlusion types because learned weak classifiers do not cover the face with the same performance. To alleviate this problem, we plan to modify the initial training by adding constraints to the weak classifier locations.
References
Huang C, Ai H, Li Y, Lao S: High-performance rotation invariant multiview face detection. Trans. Patt. Anal. Mach. Intell 2007, 29(4):671-686.
Maytal Saar-Tsechansky: Handling missing values when applying classification models. J Mach Learn Res. 2007, 8: 1623-1657.
Smeraldi F, Defoin-Platel M, Saqi M: Handling missing features with boosting algorithms for protein-protein interaction prediction. Data Integration in the Life Science, ed by. P Lambrix, G Kemp. Proceedings of the 7th International Conference, DILS 2010, Gothenburg, Sweden, August 25-27, 2010. Lecture Notes in Computer Science, vol 6254 (Springer, Berlin, 2010), pp. 132–147
Globerson A, Roweis S: Nightmare at test time: robust learning by feature deletion. In Proceedings of the 23rd International Conference on Machine Learning (ICML ’06), June 2006. New York: ACM; 2006:353-360.
Dekel O, Shamir O, Xiao L: Learning to classify with missing and corrupted features. Mach. Learn. 2008, 81: 149-178.
Chen J, Shan S, Yang S, Chen X, Gao W: Modification of the adaboost-based detector for partially occluded faces. 18th Int. Conf. Pattern Recognit. 2006, 2: 516-519.
Lin YY, Liu TL, Fuh CS: Fast object detection with occlusions. Eur. Conf. Comput. Vis. 2004, 3021: 402-413.
Schapire RE: The strength of weak learnability. Mach. Learn. 1990, 5(2):197-227.
Viola P, Jones M: Rapid object detection using a boosted cascade of simple features. Conf. Comput. Vis. Pattern Recognit. 2001, 1: 511-518.
Friedman J, Hastie T, Tibshirani R: Additive logistic regression : a statistical view of boosting. Ann. Statist. 2000, 28: 337-407.
Lefakis L, Fleuret F: Joint cascade optimization using a product of boosted classifiers. Adv. Neural Inf. Process. Syst. 2010, 23: 1315-1323.
Lin YY, Liu TL: Robust face detection with multi-class boosting. Conf. Comput. Vis. Pattern Recognit. 2005, 1: 680-687.
Schneiderman H, Kanade T: A statistical method for 3d object detection applied to faces and cars. Conf. Comput. Vis. Pattern Recognit. 2000, 1: 746-751.
Huang C, Ai H, Wu B, Lao S: Boosting nested cascade detector for multi-view face detection. Int. Conf. Pattern Recognit. 2004, 2: 415-418.
Tuzel O, Porikli F, Meer P: Human detection via classification on Riemannian manifolds. In IEEE Conference on Computer Vision and Pattern Recognition, 17–22 June 2007. Piscataway: IEEE; 2007:1-8.
Tuzel O, Porikli F, Meer P: Region covariance : a fast descriptor for detection and classification. In Proceedings of the 19th European Conference on Computer Vision, May 2006. Berlin: Springer-Verlag; 2006:589-600.
Huang GB, Ramesh M, Berg T, Learned-Miller E: Labeled faces in the wild: a database for studying face recognition in unconstrained environments. Technical Report 07-49, University of Massachusetts (2007)
Muja M, Lowe DG: Fast approximate nearest neighbors with automatic algorithm configuration. In VISAPP International Conference on Computer Vision Theory and Applications (VISAPP’09), Lisbon,5–8February 2009. Setubal: INSTICC Press; 2009:331-340.
Rowley HA, Baluja S, Kanade T: Neural network-based face detection. Trans. Patt. Anal. Mach. Intell. 1998, 20: 23-38. 10.1109/34.655647
Yao J, Odobez JM: Fast human detection from joint appearance and foreground feature subset covariances. Comput. Vis. Image Understanding 2011, 115: 1414-1426. 10.1016/j.cviu.2011.06.002
Martinez AM, Benavente R: The AR face database. Technical Report 24,. The Ohio State University, (1998)
Jones M, Viola P: Fast multi-view face detection. Technical Report 96,. Mitsubishi Electric Research Laboratories, (2003)
Lienhart R, Kuranov A, Pisarevsky V: Empirical analysis of detection cascades of boosted classifiers for rapid object detection. Pattern Recognit 2002, 2781: 297-304.
Phillips PJ, Moon H, Rizvi SA, Rauss PJ: The FERET evaluation methodology for face recognition algorithms. Trans. Patt. Anal. Mach. Intell. 2000, 22(10):1090-1104. 10.1109/34.879790
Acknowledgements
We want to thank OSEO for supporting our work which is part of the Biorafale project aimed at detecting and recognizing dangerous fans in football stadiums.
Author information
Authors and Affiliations
Corresponding authors
Additional information
Competing interests
The authors declare that they have no competing interests.
Authors’ original submitted files for images
Below are the links to the authors’ original submitted files for images.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Bouges, P., Chateau, T., Blanc, C. et al. Handling missing weak classifiers in boosted cascade: application to multiview and occluded face detection. J Image Video Proc 2013, 55 (2013). https://doi.org/10.1186/1687-5281-2013-55
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/1687-5281-2013-55






 occluded face. (b) An example of type
occluded face. (b) An example of type  occluded face.
occluded face.

 and then dispatched to McCascade to finally be detected as type
and then dispatched to McCascade to finally be detected as type  occluded face.
occluded face.







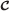 , (2) the McCascade , and (3) the detector McCascades + evidence.
, (2) the McCascade , and (3) the detector McCascades + evidence. , 2) the McCascade , and (3) the detector McCascades + evidence.
, 2) the McCascade , and (3) the detector McCascades + evidence.
 (noted Cascade), the McCascade (noted McCascade), and the association of
(noted Cascade), the McCascade (noted McCascade), and the association of  , and with the principle of cascading with evidence (noted McCascades + evidence).
, and with the principle of cascading with evidence (noted McCascades + evidence).


 . It is noted 'FDcov’ in the results.
. It is noted 'FDcov’ in the results. ,, and with the principle of cascading with evidence. It is noted 'FDcov + occlusion’ in the results.
,, and with the principle of cascading with evidence. It is noted 'FDcov + occlusion’ in the results.



