- Research
- Open access
- Published:
Supporting visual quality assessment with machine learning
EURASIP Journal on Image and Video Processing volume 2013, Article number: 54 (2013)
Abstract
Objective metrics for visual quality assessment often base their reliability on the explicit modeling of the highly non-linear behavior of human perception; as a result, they may be complex and computationally expensive. Conversely, machine learning (ML) paradigms allow to tackle the quality assessment task from a different perspective, as the eventual goal is to mimic quality perception instead of designing an explicit model the human visual system. Several studies already proved the ability of ML-based approaches to address visual quality assessment; nevertheless, these paradigms are highly prone to overfitting, and their overall reliability may be questionable. In fact, a prerequisite for successfully using ML in modeling perceptual mechanisms is a profound understanding of the advantages and limitations that characterize learning machines. This paper illustrates and exemplifies the good practices to be followed.
1. Introduction
Providing the user with an excellent experience is one of the main goals of present-day electronic multimedia devices. Any technology concerned with digital media distribution and delivery is expected to preserve or, better, to enhance the visual quality of the handled media. Nevertheless, maintaining or improving the perceived visual quality across the different stages of the distribution chain (acquisition, storage, transmission, and delivery to the user) is a challenging task, and due to technological limitations (e.g., errors in acquisition, bandwidth constraints, unreliable transmission channels), it is likely that the media reaches the user in a rather distorted appearance. As a consequence, it is important that multimedia delivery systems are equipped at different stages with means for visual quality verification and, when necessary, restoration.
To guarantee a pleasant user experience, it is essential that the control of visual quality is based on perceptually coherent criteria. Systems in charge to assess the quality of the incoming video (or image) signal should accurately reproduce perceptual mechanisms underlying the human visual system (HVS). At the same time, the eventual computational complexity of these systems is a crucial issue. When implemented in hardware circuitry for real-life applications (e.g., televisions, mobile phones, tablets), embedded devices should be able to estimate quality on the fly, after the signal receiving and before the actual visualization of the media.
A variety of methods for automated (objective) quality assessment of images and video have been proposed in the literature [1–3]. Traditional approaches usually decouple the quality assessment task into two steps, by first defining a feature-based representation of the signal, and then mapping this lower-dimensional description into quality scores. This is usually accomplished by fitting a regression function over ground truth data (i.e., subjective quality scores) [3]. Many of these approaches improve their reliability by explicitly modeling the highly non-linear behavior of the HVS; hence, they usually are complex and computationally expensive. As a result, in practice, most objective quality assessment methods prove to be either too complex for real-time applications or not accurate enough.
Machine learning (ML) methods allow to tackle the quality assessment task from a different perspective: they mimic the HVS response to quality losses rather than explicitly modeling it. Objective quality assessment based on ML paradigms conforms to the two-step approach of traditional methods, though modifying the balance between the computational efforts involved in each step. In the first step, a meaningful feature-based representation of the distortion affecting the media is defined. In the second step, the learning machine handles the actual mapping of the feature vector into quality scores and reproduces perceptual mechanisms (path (a) in Figure 1). Such an approach relies on the ability of ML tools to learn from examples, the complex, non-linear mapping function between feature vectors and quality scores. Consequently, (1) relatively simple, computationally inexpensive metrics can be designed, and (2) most of the computational power is spent in the off-line training phase of the learning machine [4]. A trained ML-based system can therefore support real-time quality assessment on an electronic device with a minimal overhead to the metric computational cost.
ML-based image/video quality assessment system. The input (distorted) signal DS and, if available, the original signal (OS) are firstrepresented in a low-dimensional feature space and then mapped into the quality space by means of a ML tool. Path (a) includes the two basic modules: 'feature extractor' and 'prediction system'; path (b) augments the framework with a module that is specifically designed to support the prediction system in the task of making a decision about the metric to be applied.
The ML-based framework is general and can support every type of perceived quality assessment. Several studies proved the effectiveness of methodologies that exploit ML tools to address both video [5–12] and image [13–24] quality assessment. Furthermore, as a major confirmation of the potential of these technologies in perceptual quality assessment, a CI-based framework has been adopted in multiple methods for audio quality assessment, including the ITU standard, PEAQ [25].
This paper provides an overview of the benefits that the use of ML can bring to the visual quality assessment (VQA) problem, in terms of both accuracy and computational complexity. In particular, the paper aims to provide an answer to some basic questions in this context, i.e., (1) what are the advantages of a ML-based approach to visual quality assessment? (2) what are the possible alternatives in deploying CI paradigms? and (3) what are the crucial issues that should be taken into account when implementing ML-based quality predictors?
To do so, on top of a detailed discussion of existing approaches, the setup of a ML-based objective quality metric will be commented and exemplified step by step.
The rest of the paper is organized as follows: Section 2 first summarizes the basic functioning of machine learning paradigms and then shows how they can be employed to support VQA. Section 3 explores more in detail the issues to be addressed when setting up a ML-based prediction system and possible solutions to overcome them. Section 4 analyzes some practical examples of the use of ML for supporting objective visual quality and provides comparison between the prediction accuracy obtained by ML-based VQA systems and the prediction accuracy obtained by state-of-the-art VQA systems. Open issues in ML-based VQA are discussed in Section 5. Finally, Section 6 makes some concluding remarks.
2. Machine learning for visual quality assessment
Over the past decades, research in ML yielded effective theoretical models, which proved successful in several applications such as computer vision [26], data mining [27], and bioinformatics [28]. This success is due to the fact that machine learning paradigms represent a powerful technology for tackling clustering, classification, and regression problems in complex non-linear domains. As such, over the last 10 years, the interest has grown within the VQA community towards using ML technologies to model the perceptual mechanisms underlying the HVS. Nevertheless, ML has its own limitations, which are easily exposed when a naive use of it is done. A prerequisite for successfully using ML is in fact a thorough understanding of the advantages and limitations that characterize learning machines and of the application-specific context. In the following subsection, we briefly summarize the basic functioning of machine learning paradigms; readers already familiar with the topic can refer directly to Section 2.2.
2.1 Basic functioning of learning machines
The learning problem is set under a probabilistic framework. Inductive learning is achieved by involving the process of learning from examples: the system induces a general rule from a set of observed instances. In its most general setting, the problem definition can be formalized using the following notation.
-
Dataset,
 , is a collection of data samples (patterns) holding N
p
input–output pairs (x
i
,y
i
).
, is a collection of data samples (patterns) holding N
p
input–output pairs (x
i
,y
i
). -
Input space,
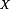 , is the space used to describe individual data items, e.g., x ∈ Rm, and
, is the space used to describe individual data items, e.g., x ∈ Rm, and 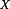 is the m-dimensional Euclidean space.
is the m-dimensional Euclidean space. -
Output space,
 , is the space of possible predictions; classification problems involve a binary setting y ∈ {−1,+1}, whereas for a regression problem, target values span a continuous range, e.g., y ∈ [−1,1].
, is the space of possible predictions; classification problems involve a binary setting y ∈ {−1,+1}, whereas for a regression problem, target values span a continuous range, e.g., y ∈ [−1,1]. -
True function, f, is the (unknown) function, y = f(x), which models the relationship between the input space
 and the output space
and the output space  .
. -
Hypothesis space,
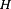 , is the set of functions that the learning algorithm examines to approximate the true function f.
, is the set of functions that the learning algorithm examines to approximate the true function f.
Inductive learning methods exploit a learning algorithm to explore the hypothesis space,  , for identifying the hypothesis h(w,x) ∈
, for identifying the hypothesis h(w,x) ∈  that best approximates the true function, f, given a set of adjusted parameters w. The learning procedure uses the examples drawn from
that best approximates the true function, f, given a set of adjusted parameters w. The learning procedure uses the examples drawn from  to select h, under the basic assumption that those examples are independent, identically distributed elements drawn from the ‘true’ distribution p() (which is stationary but unknown). In fact, a relevant constraint is that the dataset
to select h, under the basic assumption that those examples are independent, identically distributed elements drawn from the ‘true’ distribution p() (which is stationary but unknown). In fact, a relevant constraint is that the dataset  actually conveys reliable information about the unknown target function, y = f(x). The challenges in this learning problem are the following: framing a correct representation of inputs and outputs (i.e., selecting
actually conveys reliable information about the unknown target function, y = f(x). The challenges in this learning problem are the following: framing a correct representation of inputs and outputs (i.e., selecting  and
and  so that f exists [4]), sampling the problem domain (p()) in a dense enough way, and selecting the hypothesis space that best fits the given task. The basic trade‒off lies in picking out a hypothesis space that is powerful enough to support the input/output relationship, yet simple enough to be scanned efficiently.
so that f exists [4]), sampling the problem domain (p()) in a dense enough way, and selecting the hypothesis space that best fits the given task. The basic trade‒off lies in picking out a hypothesis space that is powerful enough to support the input/output relationship, yet simple enough to be scanned efficiently.
To ensure this, care should be put in selecting both the eventual set of machine adjustable parameters w and the loss function  (x,y,w) that will be used to quantify the performance of h(w,x) ∈
(x,y,w) that will be used to quantify the performance of h(w,x) ∈  . The loss function,
. The loss function,  , sets the penalty for an incorrect prediction of the input, x, by a hypothesis, h. This occurs when, for an input–output pair (x
i
,y
i
) ∈
, sets the penalty for an incorrect prediction of the input, x, by a hypothesis, h. This occurs when, for an input–output pair (x
i
,y
i
) ∈  , one obtains .
, one obtains .
2.2 ML-based visual quality assessment systems
ML is typically used to support visual quality assessment within a two-step framework. The modeling process is indeed decoupled in two tasks:
-
1.
The definition of a suitable descriptive basis for the input video signal, i.e., a feature-based description f ∈
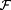 , where
, where  is a feature space (i.e., the input space X, above): (1)
is a feature space (i.e., the input space X, above): (1)S is the input signal and S′’ is the reference signal (if needed). In the (possibly low-dimensional) feature space,
 , the media can be represented in a manner that is informative with respect to its visual quality. Quality assessment systems that process both the distorted signal and the original one are referred to as full reference (FR). Instead, reduced reference (RR) systems only require a limited set of numerical features extracted from the original signal, paying the (reasonable) additional cost of transmitting side information to the video chain endpoint. No reference (NR) systems assess perceived quality without any information on the original signal [1, 2].
, the media can be represented in a manner that is informative with respect to its visual quality. Quality assessment systems that process both the distorted signal and the original one are referred to as full reference (FR). Instead, reduced reference (RR) systems only require a limited set of numerical features extracted from the original signal, paying the (reasonable) additional cost of transmitting side information to the video chain endpoint. No reference (NR) systems assess perceived quality without any information on the original signal [1, 2]. -
2.
The modeling through empirical learning of the non-linear mapping function, γ ∈
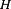 , between the feature space
, between the feature space  and a scalar measure of the perceived quality, q ∈
and a scalar measure of the perceived quality, q ∈  : (2)
: (2)where the quality score is normalized to the range [0,1] without loss of generality. It should be noticed that the true function f that γ is expected to approximate is the transfer function of the human visual system.
The first task aims at reducing the dimensionality of the original data space, which is virtually of infinite dimension, when processing video signals. The ability of the feature space,  , to characterize the underlying perceptual phenomenon is critical to the effectiveness of the overall framework. This aspect will be further discussed in Section 3.1.
, to characterize the underlying perceptual phenomenon is critical to the effectiveness of the overall framework. This aspect will be further discussed in Section 3.1.
The second task takes advantage of the ability of ML paradigms to deal with multidimensional data characterized by complex relationships, which are learned from examples using a training algorithm. This, in turn, allows to bypass the challenging issue of designing an explicit model of the perceptual mechanisms that map  into quality judgments. More details on both the selection of the model space
into quality judgments. More details on both the selection of the model space  and the actual selection of the γ (training and model selection) will be given in Section 3.
and the actual selection of the γ (training and model selection) will be given in Section 3.
Figure 1 schematizes a ML-based image quality assessment system. Path (a) includes the two basic modules: ‘feature extractor’ and ‘prediction system.’ The former module yields a vector of numerical descriptors, which the latter uses to associate a quality score with the input signal. The prediction system may include either one (single predictor setup) or an ensemble (multiple predictor setup) of learning machines trained to assess the quality score. The rationale behind using multiple predictors for quality assessment is that different types of signals might map into quality differently, and thus, using specialized predictors for each signal type would bring to more accurate quality estimations. Examples are using specialized predictors (and/or feature sets) to estimate quality losses brought about by specific distortions (e.g., compression, noise, blur) [16, 19] or to model quality preferences in a specific, narrow range of the quality scale [22].
When the prediction module involves multiple predictors, the ML-based quality assessment system is augmented with a module that gathers further information about the incoming signal (path (b) in Figure 1). Such module is specifically designed to support the prediction system in the task of making a decision about the metric to be applied (or about the strategy to be applied in combining the different metrics). The framework is quite flexible in that it can be easily adapted to both image and video signals. In the latter case, either a temporal pooling strategy is deployed at the feature extraction step (or directly by the quality prediction module) or a continuous evaluation of quality over time is performed. In this case, the feature vector f is continuously computed from the input sequence and enters the quality assessment system at the required frequency.
In practical terms, implementing the framework depicted in Figure 1 corresponds to facing three crucial issues:
-
1.
The definition of the features that describe an input signal, image, or video (the input space
 )
) -
2.
The selection of the ML tool(s) to be used to implement the prediction system h, i.e., the selection of the learning algorithm to be adopted to explore a hypothesis space

-
3.
The selection of the methods to train the system and to test its generalization performance robustly. This means defining the assembly of the dataset,
 , and the criteria to evaluate the effectiveness of a hypothesis, h, at modeling f when processing input samples not included in
, and the criteria to evaluate the effectiveness of a hypothesis, h, at modeling f when processing input samples not included in 
The next section explores more in detail these issues and possible solutions to overcome them.
3. Setting up a ML-based quality assessment system
3.1 Defining the feature space
The feature space,  , is crucial to the overall performance of the framework and involves two main issues. The first aspect concerns the significance of the feature space itself, as one requires that the space retains the relevant information to the application prediction task. If the relation between the input space and the output space is completely random, no learning can take place [4]. The feature space
, is crucial to the overall performance of the framework and involves two main issues. The first aspect concerns the significance of the feature space itself, as one requires that the space retains the relevant information to the application prediction task. If the relation between the input space and the output space is completely random, no learning can take place [4]. The feature space  should carry information on how the distortion in the image is perceived by the HVS. In other words, no ML paradigm can repair a defective feature-space design by restoring missing information.
should carry information on how the distortion in the image is perceived by the HVS. In other words, no ML paradigm can repair a defective feature-space design by restoring missing information.
The dimensionality of the feature space is the second crucial issue. If the function γ spans a high-dimensional domain, the so-called curse of dimensionality [29] may significantly affect the ability of the ML predictor to converge to the true function. The following example should clarify this aspect. Let L be the edge length of a m-dimensional hypercube in which the data samples are uniformly distributed; then, the edge length N of a hyper-cubical neighborhood that captures a fraction α of samples is given by
The graph in Figure 2 gives, for different values of α, the ratio N/L as a function of the input space dimensionality m. The graph shows that if one wants to cover 1% of the data distribution (α = 0.01) in a ten-dimensional input space, the neighborhood should be extended to more than half of L. In fact, such distorted sampling effect becomes even more apparent as the dimensionality of the input space increases, and thus, in high-dimensional spaces, any dataset of reasonable size can only sparsely populate the input space. The consequent, possible decrease in overall performance is even more important whenever a limited amount of data is available, as it is often the case in VQA (see Section 3.3.1)
In summary, the feature space  should encode all and only the information that is relevant to quality assessment. Models of the HVS have to be implemented to extract relevant features and then simplified, possibly through an appropriate feature selection procedure [4]. Feature selection [30] and/or dimensionality reduction [31] can remove noise from data and take out non-informative features, which carry either redundant or inappropriate information. This, in turn, protects the eventual prediction system against an uncontrolled increase in the computational complexity. At the same time, one can rely on ML paradigms that are less prone to curse of dimensionality, e.g., support vector machines (SVMs) [32].
should encode all and only the information that is relevant to quality assessment. Models of the HVS have to be implemented to extract relevant features and then simplified, possibly through an appropriate feature selection procedure [4]. Feature selection [30] and/or dimensionality reduction [31] can remove noise from data and take out non-informative features, which carry either redundant or inappropriate information. This, in turn, protects the eventual prediction system against an uncontrolled increase in the computational complexity. At the same time, one can rely on ML paradigms that are less prone to curse of dimensionality, e.g., support vector machines (SVMs) [32].
3.2 Selecting the ML paradigm
A huge set of ML paradigms have been proposed in the literature. Those paradigms can be categorized according to (1) the class of functions they adopt as the hypothesis space,  , and (2) the strategy they use to identify the hypothesis h that best mimics the target function, f. In practice, two main families of learning machines turned out to be popular for visual quality assessment, namely (feedforward) neural networks and kernel machines.
, and (2) the strategy they use to identify the hypothesis h that best mimics the target function, f. In practice, two main families of learning machines turned out to be popular for visual quality assessment, namely (feedforward) neural networks and kernel machines.
The regression strategy of both feedforward neural networks and kernel machines implements the decision function, as a weighted series, whose basic terms, ϕ(x), typically embed non-linear functions:
Classification machines just yield a binary output by applying the operator sign(·) to f(x).
The training procedure adjusts the degrees of freedom (i.e., the coefficients w = {w 0,w i }) in such a way that the non-linear relation (4) reproduces the desired input–output mapping. Training may prove demanding from a computational viewpoint and is typically completed off-line. The trained system, instead, can be easily implemented in an electronic device for real-time quality assessment, thanks to the straightforward expression of (4) [33].
In feedforward neural networks [34], the input–output mapping (4) is attained by arranging several elementary units (‘neurons’) into a layered structure that has no feedback between layers. The series expansion (4) of a feedforward network with a single hidden layer holding N h neurons is then expressed as
The coefficients w′ are denoted as ‘weights’, b′ is a bias, and a j (x) is a non-linear activation function. Theory proves that feedforward networks embedding a sigmoidal activation function, sigm(r) = (1 + e−r)−1, can support arbitrary mappings [35]. There is no established design criterion to dimension the parameter N h ; however, the literature provides both theoretical [36] and practical criteria [37] to address that task. The multilayer perceptron (MLP) [34] is possibly the most popular type of feedforward network. The MLP learning problem is usually tackled by the backpropagation (BP) algorithm [34], which applies a stochastic gradient-descent strategy over the weight space.
Kernel machines tackle the problem of pattern recognition by exploiting the so-called kernel trick [32]: empirical samples are projected in a high-dimensional Hilbert space, where the mapping function is easier to retrieve. A kernel function K(x i ,x j ) allows treating only inner products of pattern pairs, disregarding the specific mapping of each single pattern. As a consequence, the kernel trick allows the formulation of non-linear variants of any algorithm that can be formalized in terms of dot products.
SVMs are a very popular implementation of a kernel machine [32]. The series expansion (4) in this case is expressed in terms of kernel dot products, setting w i = α i y i , w 0 = b:
In expression (6), the ‘bias’ term b and coefficients α i should be adjusted by the training process [32]. Common choices for the kernel function K(x i ,x j ) are the radial basis function and, less frequently, the polynomial kernel. The generalization performance of a SVM depends on parameters regulating the trade-off between accuracy and complexity in the training process [32] and the kernel-specific parameters.
Although the above ML models provide a powerful way of approaching a general class of problems, the eventual behavior of the prediction system cannot be directly understood. Both feedforward neural networks and kernel machines - just as several other ML paradigms - involve the application of non-linear operators; as a result, they are often categorized as ‘black box’ approaches. In this regard, some recent work on video quality assessment [12] favored ML methodologies that could lead to ‘white box’ models, i.e., for which the predictive system can be translated into a set of intelligible rules. An interesting example of such methodologies is genetic programming (GP) [38, 39]. GP belongs to the class of evolutionary algorithms, which relies on stochastic search procedures based on the evolutionary principles such as natural selection, mutation, and reproduction. The core idea is that algorithms (i.e., models in  ) that process a predefined set of variables (i.e., the input features) through a sequence of operations can be ‘evolved’ in order to find an optimal algorithm h that best approximates f. Evolution is achieved by applying analogies of natural genetic operations (reproduction, crossover, mutation) to a population of candidate algorithms (the model space
) that process a predefined set of variables (i.e., the input features) through a sequence of operations can be ‘evolved’ in order to find an optimal algorithm h that best approximates f. Evolution is achieved by applying analogies of natural genetic operations (reproduction, crossover, mutation) to a population of candidate algorithms (the model space  ). Best algorithms are selected for reproduction based on their fitness, i.e., their performance at modeling f (which is typically defined based on the application domain). Then, they slightly mutated in order to further explore the solution space nearby the good (fittest) algorithms already found. After several iterations of the selection-reproduction-mutation process, high fitness solutions can be found. This framework, originally developed to evolve computer programs, was recently shown to be applicable to tackle ML problems [40]. There remain a number of significant open issues in the field of evolutionary computing; one of the most critical concerns is the lack of a reliable theoretical framework to provide bounds on generalization performances of the predictive system.
). Best algorithms are selected for reproduction based on their fitness, i.e., their performance at modeling f (which is typically defined based on the application domain). Then, they slightly mutated in order to further explore the solution space nearby the good (fittest) algorithms already found. After several iterations of the selection-reproduction-mutation process, high fitness solutions can be found. This framework, originally developed to evolve computer programs, was recently shown to be applicable to tackle ML problems [40]. There remain a number of significant open issues in the field of evolutionary computing; one of the most critical concerns is the lack of a reliable theoretical framework to provide bounds on generalization performances of the predictive system.
3.3 Training and model selection
A typical issue with empirical training is to obtain a high prediction accuracy while avoiding the risk of overfitting, i.e., an effective performance on the data included in the training set but a poor performance when processing unseen data. Three factors concur to effective learning:
-
1.
Training set. The training patterns should give a sufficiently large and representative sample of the data population that one wants to generalize. In fact, the generalization ability of the eventual model cannot cover samples that lie outside the distribution of the training set. Since the training set is actually a subset of the patterns included in the dataset
 , attention should be paid to the process of data collection. This is even more important in visual quality assessment, where a time-consuming process needs to be completed to associate quality scores to visual stimuli; as a major consequence, available datasets usually include a limited number of input–output pairs.
, attention should be paid to the process of data collection. This is even more important in visual quality assessment, where a time-consuming process needs to be completed to associate quality scores to visual stimuli; as a major consequence, available datasets usually include a limited number of input–output pairs. -
2.
Model selection. The settings of the machine adjustable parameters (e.g., the number of neurons N h in a feedforward neural network or the kernel function and its parameters in a SVM) determine the generalization ability of a ML model. Overly complex models exhibit higher risks of overfitting [41]. In the lack of established theoretical guidelines for model selection, one usually relies on empirical data-driven model selection criteria that proved effective [29].
-
3.
Fair estimation of the generalization performance. The accuracy at predicting quality on unseen data is the practical criterion to evaluate the effectiveness of a trained system. Generalization theory [32] provides a variety of criteria to bound the generalization error of a learning machine, but these approaches often lack practicality. The empirical measure of the error on test data still seems the most reliable method to get an accurate approximation of the system's performance.
3.3.1 Training data
It has been anticipated in Section 3 that the composition of the dataset  plays a crucial role when developing a prediction system based on ML methodologies. In visual quality assessment, datasets are sets of pairs {image, human quality score}. As human judgment represents the ground truth, collecting material for creating datasets is an expensive and time-consuming task. As a result, many datasets are not public, and those that are publicly available are of limited size. Table 1 gives an overview of some of the most popular public datasets in the area of image quality assessment (for a full overview, we demand the reader to see [42]). It summarizes their main characteristics: number of image contents, total number of distorted images involved in the subjective experiment, number of distortion types evaluated, and format of the subjective scores. For video quality assessment, two datasets are mostly used as benchmarks: the LIVE video database [43] and the EPFL video database [44]. Database [43] involves a set of 150 distorted videos created from 10 reference videos using four different distortion types: MPEG-2 compression, H.264 compression, simulated transmission of H.264 compressed bitstreams through error-prone IP networks, and through error-prone wireless networks. The EPFL video database includes a total of 78 distorted videos generated from 12 original video sequences with two spatial resolutions (CIF and 4CIF); the distorted videos have been obtained by first applying H.264 compression to the original videos and then corrupting the bistreams according to six different packet loss rates.
plays a crucial role when developing a prediction system based on ML methodologies. In visual quality assessment, datasets are sets of pairs {image, human quality score}. As human judgment represents the ground truth, collecting material for creating datasets is an expensive and time-consuming task. As a result, many datasets are not public, and those that are publicly available are of limited size. Table 1 gives an overview of some of the most popular public datasets in the area of image quality assessment (for a full overview, we demand the reader to see [42]). It summarizes their main characteristics: number of image contents, total number of distorted images involved in the subjective experiment, number of distortion types evaluated, and format of the subjective scores. For video quality assessment, two datasets are mostly used as benchmarks: the LIVE video database [43] and the EPFL video database [44]. Database [43] involves a set of 150 distorted videos created from 10 reference videos using four different distortion types: MPEG-2 compression, H.264 compression, simulated transmission of H.264 compressed bitstreams through error-prone IP networks, and through error-prone wireless networks. The EPFL video database includes a total of 78 distorted videos generated from 12 original video sequences with two spatial resolutions (CIF and 4CIF); the distorted videos have been obtained by first applying H.264 compression to the original videos and then corrupting the bistreams according to six different packet loss rates.
For both image and video data, we can notice a heterogeneity among the databases' constituency in terms of types of distortions applied to the signals to be assessed. In order to cover as many distortions as possible and increase the amount of data for training, researchers occasionally merge multiple database into a single one to determine their model and its generalization performance. However, this procedure is controversial, as merging of databases is not straightforward [50]. This aspect will be further commented in Section 5.
3.3.2 Model selection and robust estimation of the generalization performance
Cross-validation [29] represents the most robust strategy to reliably evaluate the generalization performance of a ML-based quality assessment system. As shown in Figure 3,  is randomly split into three non-overlapping subsets: a training set, TG, a validation set, VS, and a test set, TS. TG is the collection of data used for the learning procedure, whereas the validation set supports model selection. After completing several training runs for a set of tentative models h
i
∈
is randomly split into three non-overlapping subsets: a training set, TG, a validation set, VS, and a test set, TS. TG is the collection of data used for the learning procedure, whereas the validation set supports model selection. After completing several training runs for a set of tentative models h
i
∈  , the set VS is tested to evaluate the generalization performance of the various alternatives, and the model with the best performance is selected. Finally, the prediction accuracy of that model is measured on the test set TS, whose patterns have not been involved in any phase so far. It is important to understand that (1) generalization performance should be estimated once that model selection has been finalized, and (2) the patterns included in the test set should not have been involved in model selection. In fact, it is not rare that researches that exploit ML-based predictors do not provide details about the parameterization of the involved ML model or about the model selection process. This eventually undermines the reliability of the published results in terms of prediction performance.
, the set VS is tested to evaluate the generalization performance of the various alternatives, and the model with the best performance is selected. Finally, the prediction accuracy of that model is measured on the test set TS, whose patterns have not been involved in any phase so far. It is important to understand that (1) generalization performance should be estimated once that model selection has been finalized, and (2) the patterns included in the test set should not have been involved in model selection. In fact, it is not rare that researches that exploit ML-based predictors do not provide details about the parameterization of the involved ML model or about the model selection process. This eventually undermines the reliability of the published results in terms of prediction performance.
The cross-validation procedure. The dataset  is divided into three sets: the training set TG, the validation set VS, and the test set TS. Each model hypothesis h
i, i = 1,…, k is first trained on TG; its performance is then evaluated on VS. Based on this performance, the best model (in the figure, h
2) is then selected, and its performance finally estimated based on its prediction error on the data included in the test set TS.
is divided into three sets: the training set TG, the validation set VS, and the test set TS. Each model hypothesis h
i, i = 1,…, k is first trained on TG; its performance is then evaluated on VS. Based on this performance, the best model (in the figure, h
2) is then selected, and its performance finally estimated based on its prediction error on the data included in the test set TS.
As mentioned in Section 3.1, in video quality assessment, the size, N
p
, of the dataset  is usually quite small, which potentially undermines the assumption that TG - which is a subset of
is usually quite small, which potentially undermines the assumption that TG - which is a subset of  - actually is a representative sample of the population. Therefore, research often relies on a ‘multi-run’ version of the conventional cross-validation procedure. In this case, multiple iterations of the model selection procedure are performed by varying the splitting of data over the training, validation, and test sets [4]. This setup eventually gives a robust estimate of the generalization error. The k-fold strategy and the bootstrap strategy represent common approaches toward that purpose.
- actually is a representative sample of the population. Therefore, research often relies on a ‘multi-run’ version of the conventional cross-validation procedure. In this case, multiple iterations of the model selection procedure are performed by varying the splitting of data over the training, validation, and test sets [4]. This setup eventually gives a robust estimate of the generalization error. The k-fold strategy and the bootstrap strategy represent common approaches toward that purpose.
4. ML-based quality assessment: practical examples
Section 3 discussed a number of good practices to set up a ML-based quality assessment system. The goal of this section is to better illustrate those practices by analyzing some practical examples drawn from the literature. Remarkable examples of the use of ML for supporting objective visual quality assessment are reviewed according to their use of a single or multiple predictors (see Section 2.2). Section 4.1 will analyze ML-based VQA systems with a single predictor setup (path (a) in Figure 1); thus, a framework in which a single general mapping function is entitled to model the perceptual mechanism. Conversely, Section 4.2 will examine ML-based VQA systems that also include path (b); hence, the prediction system models the perceptual mechanism by exploiting different specialized mapping functions, and a supporting block drives the selection of the correct mapping function by analyzing the input signals. For the sake of clarity, Table 2 summarizes the principal characteristics of the systems that will be analyzed in the following sections. Finally, Section 4.3 will deal with a crucial point: the ability of the ML-based systems to provide a reliable estimation of the perceptual mechanisms.
4.1 Visual quality assessment by adopting a single mapping function
Coupling the feature-based description to a quality score by means of a single function is possibly the most popular approach to VQA. As such, many ML-based systems have been proposed that use a single predictor to accomplish the objective estimation of visual quality. In the domain of image quality assessment, the works published by Li et al. [18] and by Narwaria and Lin [24] provide two interesting examples of such systems.
In the NR VQA of Li et al. [18], the feature space is designed to characterize a few perceptual aspects of the image content: the degree of coherency of the local frequencies comprising the image, the available local information content of the image, and the perceptually relevant rate of change of image luminance. The prediction system is supported by the general regression neural network (GRNN, [51]), which receives as input the four features worked out from the distorted image and yields as output the corresponding quality score. A GRNN is a probabilistic neural network, which in principle can guarantee fast learning. However, the eventual trained machines may prove computationally less efficient than feedforward neural networks, as both computational complexity and memory occupation of the trained GRNN increase with the size of the training set. The LIVE database provided the dataset for both training the GRNN and evaluating the performance of the eventual prediction system. A fivefold cross-validation scheme has been adopted for this purpose, where the five folds were designed to not share any image content. The paper provides the setup of the only adjustable parameter of GRNN, the smoothness of fit σ; however, details about the model selection procedure are missing.
Narwaria and Lin [24] propose a FR ML-based framework that can be used both for image and video quality assessment. Singular value decomposition (SVD) is exploited to extract meaningful perceptual-related information from images (or video frames). In practice, SVD is used to remap the image (i.e., a matrix) into a coordinate system where the covariance matrix is diagonal. As a result, an input matrix I of size r × c is factorized as follows: I = U·S·Vt, where U is a r × r orthogonal matrix and V is a c × c orthogonal matrix. S is an r × c matrix whose off-diagonal entries are all 0's and whose diagonal elements are the singular values, which appear in descending order. The feature space  is designed to represent the difference between (a) the matrixes U, S, and V as obtained from the original image and (b) the corresponding matrixes that are obtained from the distorted version of that image. This eventually results in a 2B-dimensional feature space; here, B is a parameter that characterizes the feature extraction process, which firstly operates on a local basis (B × B blocks) and then aggregates information to generate a single image descriptor. In the paper, the authors set the value of B to 128. A SVM is employed to implement the prediction system; such choice is possibly motivated by the need to exploit a ML paradigm that is less prone to the curse of dimensionality, which may represent a major issue when dealing with a 256-dimensional input space. The overall framework is validated through a very robust setup. In the image quality assessment configuration, the dataset
is designed to represent the difference between (a) the matrixes U, S, and V as obtained from the original image and (b) the corresponding matrixes that are obtained from the distorted version of that image. This eventually results in a 2B-dimensional feature space; here, B is a parameter that characterizes the feature extraction process, which firstly operates on a local basis (B × B blocks) and then aggregates information to generate a single image descriptor. In the paper, the authors set the value of B to 128. A SVM is employed to implement the prediction system; such choice is possibly motivated by the need to exploit a ML paradigm that is less prone to the curse of dimensionality, which may represent a major issue when dealing with a 256-dimensional input space. The overall framework is validated through a very robust setup. In the image quality assessment configuration, the dataset  is obtained using eight different databases, according to two different setups. First, the overall framework is trained and then tested on each of the eight datasets separately. A k-fold cross-validation strategy is adopted for each of the eight different experiments, with k set depending on the number of reference images in the datasets. Also in this case, folds are designed so that no reference images (and their distorted versions) are shared among them. In a second setup, cross-database performance is evaluated by training the SVM on the features extracted from the images of one dataset; then, the model is tested on the images of another dataset. Finally, the ability of the proposed framework to deal with video quality assessment is evaluated by training the system with the image databases and then using the LIVE video database and the EPFL video database as test sets.
is obtained using eight different databases, according to two different setups. First, the overall framework is trained and then tested on each of the eight datasets separately. A k-fold cross-validation strategy is adopted for each of the eight different experiments, with k set depending on the number of reference images in the datasets. Also in this case, folds are designed so that no reference images (and their distorted versions) are shared among them. In a second setup, cross-database performance is evaluated by training the SVM on the features extracted from the images of one dataset; then, the model is tested on the images of another dataset. Finally, the ability of the proposed framework to deal with video quality assessment is evaluated by training the system with the image databases and then using the LIVE video database and the EPFL video database as test sets.
The thorough testing procedure followed by Narwaria et al. is to be regarded as a best practice to correctly estimate the generalization ability of ML-based VQAs. Unfortunately, an aspect that the paper does not seem to address properly is model selection: both in the case of image quality assessment and video quality assessment details are not provided about the setup of the three adjustable parameters that characterize the proposed SVM-based prediction system.
Further attempts of designing VQA systems based on a single ML predictor were made, e.g., by Liu et al. [17], who used a feedforward neural network to predict the mean opinion scores (MOS) of images distorted with JPEG compression and blur. In [14], second-order histograms were used to characterize distortion perception, and then a PCA was adopted to select the most significant features. An extreme learning machine [52], i.e., an extension of the classic multilayer perceptron paradigm, was used to accomplish the final mapping due to its high non-linear modeling capabilities.
In the video domain, support vector machines have been used to predict the visibility of packet loss artifacts [53], whereas circular backpropagation (CBP, [54]) neural networks have supported the prediction of the annoyance brought about by MPEG artifacts [6]. Le Callet and others [8] used instead a time-delay neural network for video quality assessment as it has the ability to represent a relationship between events in time.
Recently, Staelens et al. [12] proposed an interesting and novel approach to NR VQA. They propose a framework that (1) does not require a complete decoding of the received video stream to estimate perceived quality and (2) makes use of a white box ML paradigm, the GP-based symbolic regression method [38]. The authors use a tree-based regression model to represent the mapping function γ, where a set of predefined operators (e.g., summation, multiplication) combine a set of candidate features directly computable from the encoded bitstream. Trees are evolved in order to optimize the fitness function, which evaluates both the tree performance in predicting the MOS, and its complexity (i.e., its number of nodes). In this way, accurate but simple models are privileged in the evolution. The resulting model is based on 4 of the initial 42 features, and its functioning is transparent, as the operations performed by the tree are observable. As a result, the feature selection process is combined with the learning process in an elegant way.
4.2 Visual quality assessment by adopting multiple mapping functions
The second category of models we are interested in analyzing is that of VQA using multiple predictors to accomplish quality estimation. The rationale behind this setup is that not all types of signals map into quality in the same way. For example, it has been shown that videos with different quality levels are evaluated according to different criteria [55]. Also, it is well known that sensitivity and annoyance to different distortions follow different perceptual mechanisms. As a result, in some cases, it might be appropriate to first identify the type of signal whose quality has to be evaluated and then use a specialized predictor trained to assess quality related to the specific characteristics of that signal type. The works published by Redi et al. [16], Moorthy and Bovik [19], and Charrier et al. [22], all dealing with image quality assessment, represent interesting examples of such setup.
The system presented in [16] exploits different specific mapping functions tuned to address a specific image distortion among a set of candidate ones. This strategy has been adopted by multiple studies in the literature, such as [21] and [56]; thus, it is worthwhile to analyze in detail. In [16] and according to the scheme proposed in Figure 1, a dedicated block is designed to analyze the incoming signals and to identify the predictor to be applied. The feature space is designed to capture the effect of structural distortions on color distribution. First, color correlograms are computed for a set of non-overlapping blocks of the images (original and distorted); then, from each correlogram, statistical features that summarize the changes in the structure of the block are extracted. Global-level feature information is then obtained by extracting the envelope of the distribution of each feature across the image, i.e., using percentiles to aggregate block-based information. The authors adopt a feature selection procedure based on the Kolmogorov-Smirnov test to select from the candidate features those that more informatively characterize the perceptual phenomenon. This results in a 30-dimensional vector characterizing both the input image and the reference image. Such vector first enters a SVM-based distortion identification module, working as multiclass classifier. The authors adopted a standard approach to implement this module, which exploits d one-versus-rest classifiers (d being the number of distortions), i.e., classifiers that are designed to solve the binary problem ‘one distortion versus the others’. Once the distortion has been identified, the input vector is forwarded to the corresponding mapping function, taken out of a set of predictors modeled by exploiting CBP networks [54]. These networks belong to the family of feedforward neural networks and provide an effective tool to tackle regression tasks. A fivefold cross-validation strategy was used to evaluate the generalization performance of the trained objective assessment system; the LIVE database provided the dataset  . Indeed, the paper [16] also analyzes the generalization performance of the two ML-based blocks separately and discusses model selection details.
. Indeed, the paper [16] also analyzes the generalization performance of the two ML-based blocks separately and discusses model selection details.
The framework proposed by Moorthy and Bovik [19] uses natural scene statistics to tackle NR image quality assessment. Analogously to [16], the prediction system includes different distortion-specific mapping functions. However, in this case the final quality score for an input image is predicted by combining the outcomes of the different mapping functions. To this purpose, a specific module is designed to provide a probabilistic distortion identification estimate that eventually drives the prediction system. In [19], the authors structure an 88-dimensional feature space. Those features are obtained by exploiting the peculiarities of wavelet transforms, which can perform mirror models of spatial decompositions occurring in the V1 area of the primary visual cortex. The steerable pyramid decomposition [57] over two scales and six orientations is exploited to this purpose. SVMs provide the ML paradigm to support both the ‘probabilistic distortion identification’ block and the ‘quality prediction’ block. The former block exploits SVMs to provide - for each candidate distortion - the probability that the input image is affected by that distortion; in fact, the paper does not discuss the details of the implementation of this module. The latter block uses SVMs to implement the distortion-specific mapping functions. The approach was cross-dataset validated, based on the LIVE for training and model selection and on the TID2008 for evaluating the generalization performance of the framework. The paper does not supply details about the parameterization assigned to the SVM-based predictors after model selection.
Charrier and others [22] also proposed a multiple predictor system, but with a different flavor. In this case, the selector module aims at dividing the quality scale in five sectors, each corresponding to a specialized mapping function for that quality range. The underlying assumption is that different perceptual mechanisms are involved when one judges a heavily degraded image or a slightly degraded image [55]. The feature space includes 25 quantities, which belong to two categories: spatial criteria and spatial frequency criteria. The first category involves features integrated in the multi-scale structural similarity index (MS-SSIM) proposed in [58]; the second category exploits features derived from the steerable pyramid decomposition of the image. Both the classification block that select the mapping function to be applied and the prediction system have been implemented using SVMs. The selection module is obtained using the theory of evidence framework [59]: the eventual decision is finalized by taking into account the confidence associated to the outputs of ten binary SVM-based classifiers, which correspond to the ten binary problems that stem from a problem with five classes. The mapping functions supporting the prediction system are modeled using SVM as regression tool. The authors used a subset of the LIVE database to complete training and model selection, while the remaining part of the LIVE database and the TID2008 database have been used as test set. Details concerning the parameterization of the ML-based models, as obtained after model selection, are not reported.
4.3 Performance: ML-based approaches versus state-of-the-art systems
The performance of a VQA system should be evaluated by estimating its prediction accuracy. While other factors may play an important role (e.g., computational complexity of the system and technical feasibility of implementation into consumer electronic devices), the ability of the system to reliably assess subjective perception of quality represents without doubt the first element to be analyzed. In the context of the present paper, indeed, the key point is the comparison between the prediction accuracy obtained by ML-based VQA systems and the prediction accuracy obtained by state-of-the-art VQA systems.
As detailed in the previous sections, it is uneasy to compare the performance of ML-based VQA systems, as most of them adopt a different testing setup. In the area of image quality assessment, however, it is common to adopt the SSIM index [60] as benchmark. Indeed, most of the works analyzed above (and listed in Table 2) report a comparison of the performance of their proposed algorithm with it. To give a general overview of ML-based VQA performance, we summarize in Tables 3 and 4 the (available) Pearson's correlation coefficient and Spearman's correlation coefficient (SROCC) [3] between the quality scores predicted by SSIM and the systems in Table 2 and the human quality scores. We then detail better the single metric performance below.
For the sake of completeness, two important aspects should be addressed before starting the discussion about the performances. First, as anticipated above, most of the works listed in Table 2 do not provide clear statements about model selection outcomes; this actually hinders the reproducibility of the experiments. Second, in a few cases, the authors estimated the performance of state-of-the-art algorithms on the proposed experiments by exploiting the available Matlab routines; in other case, though, the performance associated to state-of-the-art algorithms has been obtained by considering the numerical results already provided in the literature.
In [24], Narwaria and Lin compared their FR system with the SSIM algorithm on seven different experiments involving as many image databases; the results provided in the paper show that their framework was able to attain a better Pearson's correlation coefficient than SSIM in all the experiments. The paper also reported on the results obtained with experiments involving cross-database evaluation, as discussed in Section 4.1; in this case, a comparison with SSIM has not been proposed. Indeed, it is interesting to note that numerical results proved that the performance of the proposed framework somewhat decreased when TID2008 is used as test set. Such outcome is not surprising: this database involves a few distortion types that are not addressed in other databases; hence, the ML-based predictor is required to model portions of the p(,) that the training set covered only partially.
The performance of the FR approach presented by Charrier et al. in [22] is documented through a comparison with SSIM on two different experiments; SROCC was adopted as performance indicator. The first experiment involved the LIVE database: the results show that the proposed system was able to slightly outperform SSIM. The second experiment addressed cross-database evaluation: the LIVE database was used as training set and the TID2008 database was used as test set. Two are the interesting outcomes of this experiment. First, the performance on the cross-database evaluation is not as good as the performance on the LIVE database; however, as already discussed, this behavior may partially be ascribed to the characteristics of the TID2008 database. Second, the proposed system seems still able to outperform the SSIM algorithm.
Redi et al. [16] used the LIVE database to estimate the performance of their RR system; indeed, they provided a comparison with the SSIM algorithm based on the Pearson's correlation coefficient. In this regard, one should take into account that SSIM is a FR metric; thus, the comparison is not completely fair. However, the results show that the proposed system compares favorably with SSIM, which outperforms noticeably the RR metric only when JPEG2000 compression is involved.
Two different approaches for NR quality assessment are proposed in the works by Li et al. [18] and by Moorthy and Bovik [19]. The first approach exploits a small set of features and a single mapping function, while the second approach utilizes a 88-dimensional feature space and multiple distortion-oriented mapping functions. In [18], the performance of the proposed system has been evaluated using the LIVE dataset. A comparison with the NR algorithm BIQI [61] has been provided; Pearson's correlation coefficient, SROCC, and root mean square error (RMSE were used as performance indicators. The results prove that the proposed system in general was able to obtain the same performance as BIQI; in fact, BIQI was evidently outperformed when considering the RMSE indicator.
In [19], performance evaluation comprised two different experiments. In the first, only the LIVE database has been involved. The second addressed cross-database evaluation, with LIVE database as training set and TID2008 database as test set; indeed, in this case, the experiment involved only the images of TID2008 that were corrupted with the distortions also covered by LIVE. For the first experiment, the paper reported the comparison with two different versions of the BIQI algorithm and with the BLIINDS [62] algorithm; Pearson's correlation coefficient, SROCC, and RMSE were used as performance indicators. The results show that the proposed ML-based framework was able to markedly outperform state-of-the-art approaches. For the second experiment, only a comparison with the FR metric SSIM has been reported. In this case, results show that SSIM attained a better performance in terms of SROCC; however, one should consider that the comparison involve a FR metric and a NR metric.
In the area of video quality assessment, usually the video quality metric (VQM) [63] is adopted as benchmark. In [12], Staelens et al. presented a comparison between their FR framework and the VQM metric; the EPFL database provided the test set, while the framework was trained using eight video sequences not belonging to standard benchmarks. The results show that the GP-based system compared favorably with VQM both in terms of Pearson's correlation coefficient and SROCC. The FR VQA system proposed in [24] by Narwaria and Lin can actually also deal with video signals. The paper reported on the results of performance evaluations that involved the LIVE video database and the EPFL database; however, a comparison with VQM has not been provided. An analysis of those results shows that the proposed ML-based framework was able to obtain a suitable prediction accuracy on the EPFL videos (Pearson's correlation coefficient close to 0.9). On the other hand, results are less satisfactory on the LIVE videos (Pearson's correlation coefficient lower than 0.8).
The overall outcome of this summary analysis seems to be the following: studies published in the literature show that quality assessment systems that exploit ML paradigms can attain prediction accuracy comparable to or even higher than what is found with state-of-the-art methodologies. This is a key aspect, which in turn confirms that ML tools can play an important role in the area of visual quality assessment. The interesting point is that the works listed in Table 2 cover a wide range of approaches, which differ in terms of features, ML tools, and overall scheme of the prediction system. Indeed, they all proved able to compare favorably with ‘conventional’ approaches to VQA. On the other hand, a few open issues remain that need to be addressed before ML can be considered a reliable option for the development of VQA systems. These issues will be discussed in Section 5.
5. Open issues in ML-based visual quality assessment
VQA systems can take advantage of the ability of ML paradigms to deal with non-linear, complex domain. Section 4 showed (1) that ML-based frameworks in general compare favorably with state-of-the-art metrics and (2) that ML models provide flexible yet effective tools to support various approaches to the design of the predictive system. Moreover, ML paradigms do not represent a hindrance to the implementation of quality assessment systems in consumer electronic devices. The literature indeed provides several design approaches for the implementation of ML tools in analog or digital hardware [33]. In recent years, though, the focus of ML hardware design shifted towards implementations on reconfigurable digital hardware, i.e., field programmable gate arrays http://enpub.fulton.asu.edu/resp/vpqm/vpqm12/" (FPGAs) [33]. This allows for more flexibility with respect to network size, type, topology, and other constraints while maintaining increased processing density by taking advantage of the natural parallel structure of neural networks [33]. Currently, FPGAs provide performance and logic density similar to ASIC but with the flexibility of quick design/test cycles.
On the other hand, one should take into account that a few critical issues remain to be discussed:
-
Feature space. The analysis of the existing ML-based approaches to VQA proposed in Section 4 seems to indicate that in most cases the design of the feature space follows a ‘cumulative’ criterion. One selects a set of features that are possibly correlated with the perceptual mechanisms to be modeled, without any deep investigation on the amount of redundancy involved or on the presence of irrelevant attributes. The underlying hypothesis often is that ‘the more features, the better’. However, as shown in Section 3, such an approach may eventually affect the performance of the prediction system because of the curse of dimensionality. In general, a ML paradigm is not designed to provide feature selection abilities, and this step has to be made explicitly. However, one can rely on powerful solutions that combine ML with feature selection [30], as in the case of the work by Staelens et al. [12]. As several ML-based approaches to VQA somewhat underestimate this aspect, one would even expect that better prediction performance may be obtained by involving feature selection procedures into the design process. In this regard, one should also consider that the number of features to be extracted from the incoming signal impacts on the computational complexity of the prediction system.
-
Model selection. This aspect possibly represents the most critical concern. The great majority of the works published in the literature does not provide essential details about this procedure. In fact, the setup of machine adjustable parameters is a central step for any predictive model, whether based on ML or not. Moreover, a fair evaluation of the model's ability to predict unseen patterns can only be completed once those parameters have been set. In the case of ML-based VQA frameworks, the unavailability of parameter settings actually hampers the reproducibility of the experiments. Therefore, future works should carefully address this issue to the purpose of improving the reliability of ML-based prediction systems.
-
Design of the prediction system. Several frameworks adopted SVM to implement the regression functions that support the actual mapping between the feature space and the quality score. Two factors possibly contribute to this choice: (1) SVM is a very popular yet powerful paradigm, and (2) SVM can deal with the curse of dimensionality, which represents a major issue when the feature space is high dimensional. A third factor that might indeed favor the use of SVM is the public availability of off-the-shelf software implementations of support vector-based models, such as LibSVM [64], which allow the immediate use of these tools. However, while SVM can be considered the most effective classification model available in the ML area, several powerful options exist to tackle regression problems; in this regard, the works by Redi et al. [16], Le Callet et al. [8], and Staelens et al. [12] represent interesting examples.
A few additional issues that might be worthwhile addressing involve more in general the setup of VQA systems. A first aspect that should be mentioned is that conventional metrics as well stem from parametric models. This in turn means that the setup of the parameters that characterize the metric usually is the result of data-driven procedure. In this sense, it is useful to analyze the results of cross-database experiments that involve TID2008 database as test set. State-of-the-art metrics - just as ML-based metrics - exhibit a decrease in the prediction performance that is related to the presence of distortions that were not involved in the setup of the prediction system. The reason for this might lie in the fact that different databases describe different types of data populations. The experimental methodology [65] with which human quality scores are collected largely varies across databases, with consequent loss of comparability of the data [50, 66]. On top of this, human quality scores can be reported in different ways, e.g., mean opinion scores and differential mean opinion scores (DMOS), measuring at times impairment annoyance and at times overall quality [65]. These judgments represent different psychophysical quantities, not necessarily linearly related. Such inconsistencies among datasets may actually represent a problem when dealing with ML methodologies, since databases cover different signal populations and sample the relationship (signal, quality judgment) in a non-uniform way. As a result and as mentioned in Sections 2.1 and 3.1, obtaining (ML-based) models that generalize over different databases might prove difficult.
Finally, an aspect that should be taken into account in using learning machines to support visual quality assessment is that the loss function  based on which the models in
based on which the models in  are optimized typically measures the prediction error (i.e., the difference between the predicted quality score and the actual human quality score). As a result, the models are optimized to predict the actual absolute values of the subjective quality scores. On the other hand, quality assessment systems are also judged on how well the scores they predict correlate with subjective judgments [3], independent on their absolute value. Researchers in VQA that intend to use ML to support their prediction systems should keep this discrepancy into account, and research is needed to develop ML methods whose risk function takes into account prediction consistency and monotonicity, besides value accuracy.
are optimized typically measures the prediction error (i.e., the difference between the predicted quality score and the actual human quality score). As a result, the models are optimized to predict the actual absolute values of the subjective quality scores. On the other hand, quality assessment systems are also judged on how well the scores they predict correlate with subjective judgments [3], independent on their absolute value. Researchers in VQA that intend to use ML to support their prediction systems should keep this discrepancy into account, and research is needed to develop ML methods whose risk function takes into account prediction consistency and monotonicity, besides value accuracy.
6. Conclusions
In this paper, we analyzed advantages and disadvantages of using machine learning to support visual quality assessment. Through an analysis of the approaches existing in the literature, we reviewed the common characteristics of ML-based VQA, showing how these methods can achieve comparable if not better performance than traditional methods and pointing out the issues that can expose the reliability of these systems. Overall, the use of ML in VQA seems very promising; however, more research is needed in order to improve several aspects. First, perception-oriented feature selection strategies should be developed and deployed to avoid the risk of falling into the curse of dimensionality; second, robust validation procedures should be established to test these systems, including fixed steps such as model selection and fair evaluation of the generalization error. Finally, a core issue in establishing reliable ML-based VQA is the availability of training data; in this sense, developing either realignment procedures [50] or subjective methodologies that allow the collection of comparable quality scores across different experiments (e.g., [66]) is desirable.
Future directions in ML-based VQA should include the extension of this approach to emerging topics such as 3D video and saliency maps. Indeed, researchers belonging to the communities of multimedia signal processing and machine learning should also focus on the adoption of semi-supervised learning models into VQA systems. In semi-supervised learning [67], one exploits both unlabeled and labeled data to learn empirically the true function f; as a major result, the semi-supervised approach should improve over the model that is learnt by only using labeled data. In recent years, the interest in semi-supervised learning has increased, especially because several application domains exist in which large datasets are available but labeling is difficult, expensive, or time consuming: text mining, natural language processing, image and video retrieval, and bioinformatics. VQA can easily be associated to such domains; as such, we believe that semi-supervised machine learning approaches can bring significant added value to the field.
References
Hemami SS, Reibman AR: No-reference image and video quality estimation: applications and human-motivated design. Signal Processing: Image Commun 2010, 25(7):469-481. 10.1016/j.image.2010.05.009
Lin W, Jay Kuo C-C: Perceptual visual quality metrics: a survey. J. Visual Commun. Image Representation 2011, 22(4):297-312. 10.1016/j.jvcir.2011.01.005
VQEG, Final report from the video quality experts group on the validation of objective models of video quality assessment. 2003. . Accessed 3 September 2013 http://www.vqeg.org/
Gastaldo P, Redi JA: Machine learning solutions for objective visual quality assessment. Paper presented at the 6th international workshop on video processing and quality metrics for consumer electronics, VPQM-12. Scottsdale; 2012. http://enpub.fulton.asu.edu/resp/vpqm/vpqm12/
Lin F-H, Mersereau RM: Rate–quality tradeoff MPEG video encoder. Signal Processing: Image Commun 1999, 14: 297-309. 10.1016/S0923-5965(98)00014-9
Gastaldo P, Rovetta S, Zunino R: Objective quality assessment of MPEG-2 video streams by using CBP neural networks. IEEE Trans. on Neural Networks 2002, 13(4):939-947. 10.1109/TNN.2002.1021894
Yao S, Lin W, Lu Z, Ong E, Yang X: Video quality assessment using neural network based on multi-feature extraction. Proceedings of the SPIE, Lugano, vol. 5150. In Visual Communications and Image Processing. Edited by: Ebrahimi T, Sikora T. SPIE, Bellingham; 2003:604.
Le Callet P, Viard-Gaudin C, Barba D: A convolutional neural network approach for objective video quality assessment. IEEE Trans Neural Networks 2006, 17(5):1316-1327. 10.1109/TNN.2006.879766
Kanumuri S, Cosman P, Reibman A, Vaishampayan V: Modeling packet-loss visibility in MPEG-2 video. IEEE Transactions on Multimedia 2006, 8(2):341-355.
El Khattabi H, Tamtaoui A, Aboutajdine D: Video quality assessment measure with a neural network. Int. J. Comput. Inf. Eng 2010, 4(3):167-171.
Narwaria M, Lin W, Anmin L: Low-complexity video quality assessment using temporal quality variations. IEEE Trans Multimedia 2012, 14(3):525-535.
Staelens N, Deschrijver D, Vladislavleva E, Vermeulen B, Dhaene T, Demeester P: Constructing a no-reference H.264/AVC bitstream-based video quality metric using genetic programming-based symbolic regression. IEEE Trans on Circuits Systems Video Technol 2013, 23(8):1322-1333.
Gastaldo P, Zunino R: Neural networks for the no-reference assessment of perceived quality. SPIE J Electron Imaging 2005, 14: 033004. 10.1117/1.1988313
Suresh S, Babu RV, Kim HJ: No-reference image quality assessment using modified extreme learning machine classifier. Applied Soft Computing 2009, 9: 541-552. 10.1016/j.asoc.2008.07.005
Narwaria M, Lin W: Objective image quality assessment based on support vector regression. IEEE Trans. Neural Networks 2010, 21(3):515-519.
Redi J, Gastaldo P, Heynderickx I, Zunino R: Color distribution information for the reduced-reference assessment of perceived image quality. IEEE Trans. Circ. Syst. Video Technol 2010, 20(12):1757-1769.
Liu H, Redi J, Alers H, Zunino R, Heynderickx I: An efficient neural-network based no-reference approach to an overall quality metric for JPEG and JPEG2000 compressed images. SPIE J. of Elect. Imaging 2011, 20(4):1-15.
Li C, Bovik AC, Wu X: Blind image quality assessment using a general regression neural network. IEEE Trans Neural Networks 2011, 22(5):793-799.
Moorthy AK, Bovik AC: Blind image quality assessment: from natural scene statistics to perceptual quality. IEEE Trans. Image Proc 2011, 20(12):3350-3364.
Tang H, Joshi N, Kapoor A IEEE Conference on Computer Vision and Pattern Recognition, Colorado Springs. In Learning a blind measure of perceptual image quality. IEEE, Piscataway; 2011:305.
Decherchi S, Gastaldo P, Redi J, Zunino R, Cambria E: Circular-ELM for the reduced-reference assessment of perceived image quality. Neurocomputing 2013, 102: 78-89.
Charrier C, Lézoray O, Lebrun G: Machine learning to design full-reference image quality assessment algorithm. Signal Processing: Image Communication 2012, 27: 209-219. 10.1016/j.image.2012.01.002
Narwaria M, Lin W, Enis A: Cetin, Scalable image quality assessment with 2D mel-cepstrum and machine learning approach. Pattern Recognition 2012, 45: 299-313. 10.1016/j.patcog.2011.06.023
Narwaria M, Lin W: SVD-based quality metric for image and video using machine learning. IEEE Trans. on Systems, Man and Cybernetics, Part B. Cybernetics 2012, 42(2):347-364.
Thiede T, Treurniet W, Bitto R, Schmidmer C, Sporer T, Beerends J, Colomes C, Keyhl M, Stoll G, Brandenburg K, Feiten B: PEAQ—the ITU standard for objective measurement of perceived audio quality. J. Audio Eng. Soc 2000, 48(1/2):3-29.
Sebe N, Cohen I, Garg A, Huang TS: Machine Learning in Computer Vision. Springer, Dordrecht; 2005.
Da San Martino G, Sperduti A: Mining structured data. IEEE Comput. Intell. Mag 2010, 5: 42-49.
Rajapakse JC, Zhang Y-Q, Fogel GB IEEE/ACM Transactions on Computational Biology and Bionformatics. Computational intelligence approaches in computational biology and bioinformatics, vol 4 2007.
Bishop CM: Pattern Recognition and Machine Learning. Springer, Dordrecht; 2006.
Guyon I, Elisseeff A: An introduction to variable and feature selection. J. Mach. Learn. Res 2003, 3: 1157-1182.
van der Maaten L, Postma E, van den Herik J: Dimensionality reduction: a comparative review. J Mach. Learn. Res 2009, 10: 1-41.
Vapnik V: Statistical Learning Theory. Wiley, New York; 1998.
Misra J, Saha I: Artificial neural networks in hardware: a survey of two decades of progress. Neurocomputing 2010, 74: 239-255. 10.1016/j.neucom.2010.03.021
Rumelhart DE, McClelland JL: Parallel Distributed Processing. MIT Press, Cambridge; 1986.
Hornik K, Stinchcombe M, White H: Multilayer feedforward networks are universal approximators. Neural Networks 1989, 2(5):359-356. 10.1016/0893-6080(89)90020-8
Baum EB, David H: What size net gives valid generalization? Neural Comput 1989, 1(1):151-160. 10.1162/neco.1989.1.1.151
Widrow B, Lehr MA: 30 years of adaptive neural networks: perceptron Madaline and back propagation. Proc. IEEE 1990, 78(9):1415-1442. 10.1109/5.58323
Koza JR: Genetic programming as a means for programming computers by natural selection. Stat Comput 1994, 4(2):87-112.
Filho JLR, Treleaven PC, Alippi C: Genetic-algorithm programming environments. IEEE Computer 1994, 27(6):28-43.
Espejo PG, Ventura S, Herrera FG: A survey on the application of genetic programming to classification. IEEE Trans. Systems, Man, and Cybernetics, Part C: Applications and Reviews 2010, 40(2):121-144.
Moody JE: The effective number of parameters: an analysis of generalization and regularization in nonlinear learning systems. In Advances in Neural Information Processing Systems 4. Edited by: Moody JE, Hanson SJ, Lippmann RP. Morgan Kaufmann, San Mateo; 1992:847.
Fliegel K, Timmerer C: WG4 Databases Whitepaper v1.5: QUALINET multimedia database enabling QoE evaluations and benchmarking (QUALINET, COST Action IC1003, 2013). . Accessed 3 September 2013 http://dbq-wiki.multimediatech.cz/_media/qi0306.pdf
Seshadrinathan K, Soundararajan R, Bovik A, Cormack L: Study of subjective and objective quality assessment of video. IEEE Trans. Image Process 2010, 19(6):1427-1441.
Simone F, Naccari M, Tagliasacchi M, Dufaux F, Tubaro S, Ebrahimi T Proceedings of the 1st International Workshop on Quality of Multimedia Experience, QoMEX 2009, San Diego. In Subjective assessment of H.264/AVC video sequences transmitted over a noisy channel. IEEE, Piscataway; 2009:204.
LIVE Image Quality Assessment Database (Laboratory for Image & Video Engineering, The University of Texas at Austin). . Accessed 3 September 2013 http://live.ece.utexas.edu/research/quality/
Ponomarenko N, Carli M, Lukin V, Egiazarian K, Astola J, Battisti F Proceedings of IEEE 10th Workshop on Multimedia Signal Processing, Cairns. In Color image database for evaluation of image quality metrics. IEEE, Piscataway; 2008:403.
Larson E, Chandler D: Most apparent distortion: full-reference image quality assessment and the role of strategy. SPIE J. on Electron. Imag 2010, 19(1):011006. 10.1117/1.3267105
Subjective Quality Assessment IRCCyN/IVC Database (IVC, Institut de Recherche en Communications et Cybernétique de Nantes). . Accessed 3 September 2013 http://www2.irccyn.ec-nantes.fr/ivcdb/
Image Quality Evaluation Database (MICT, University of Toyama). . Accessed 3 September 2013 http://160.26.142.130/toyama_database.zip
Pinson MH, Wolf S: Comparing subjective video quality testing methodologies. Proceedings of the SPIE, Lugano. In Visual Communications and Image Processing, vol. 5150. Edited by: Ebrahimi T, Sikora T. SPIE, Bellingham; 2003:573.
Specht DF: A general regression neural network. IEEE Trans. Neural Networks 1991, 2(6):568-576. 10.1109/72.97934
Huang G-B, Wang D, Lan Y: Extreme learning machines: a survey. Int. J. Mach. Learn. Cybern 2011, 2(2):107-122. 10.1007/s13042-011-0019-y
Argyropoulos S, Raake A, Garcia M-N, List P: No-reference video quality assessment of SD and HD H.264/AVC sequences based on continuous estimates of packet loss visibility. In Proceedings of the 3rd International Workshop Quality of Multimedia Experience, QoMEX 2011, Mechelen. IEEE, Piscataway; 2011:31.
Ridella S, Rovetta S, Zunino R: Circular back-propagation networks for classification. IEEE Trans. Neural Networks 1997, 8(1):84-97. 10.1109/72.554194
Strohmeier D, Kunzem K, Göbel K, Liebetrau J: Evaluation of differences in quality of experience features for test stimuli of good-only and bad-only overall audio visual quality. Proceedings of the SPIE, Burlingame, 3. In Image Quality and System Performance X, vol. 8653. Edited by: Burns PD, Triantaphillidou S. SPIE, Bellingham; 2013. doi:10.1117/12.2001363
Chetouani A, Beghdadi A: Image quality assessment based on distortion identification. Proceedings of the SPIE, San Francisco. In Image Quality and System Performance VIII, vol. 7867. Edited by: Farnand SP, Gaykema F. SPIE, Bellingham; 2011. doi:10.1117/12.876308
Simoncelli EP, Freeman WT, Adelson EH, Heeger DJ: Shiftable multiscale transforms. IEEE Trans. Inf. Theory 1992, 38(2):587-607. 10.1109/18.119725
Wang Z, Bovik AC: A universal quality index. IEEE Transactions on Image Processing 2002, 9(3):81-84.
Dempster A: Upper and lower probabilities induced by multi-valued mapping. Annals of Math. Stat 1967, 38: 325-339. 10.1214/aoms/1177698950
Wang Z, Bovik A, Sheikh H, Simoncelli E: Image quality assessment: from error measurement to structural similarity. IEEE Trans. Image Process 2004, 13(1):1-14.
Moorthy AK, Bovik AC: A two-step framework for constructing blind image quality indices. IEEE Signal Processing Letters 2010, 17(5):513-516.
Saad MA, Bovik AC: Blind image quality assessment: a natural scene statistics approach in the DCT domain. IEEE Transactions on Image Processing 2012, 21(8):3339-3352.
International Telecommunication Union (ITU): Objective perceptual video quality measurement techniques for digital cable television in the presence of a full reference. Rec J 2004., 144:
Chang C-C, Lin C-J: LIBSVM: a library for support vector machines. ACM Trans. on Intelligent Systems and Technology 2011, 2(3):1-39. doi:10.1145/1961189.1961199
International Telecommunication Union (ITU): BT.500–11: Methodology for the Subjective Assessment of the Quality of Television Pictures. ITU, Geneva; 2002.
Redi J, Liu H, Zunino R, Heynderickx I: Comparing subjective image quality measurement methods for the creation of public databases. Proceedings of the SPIE, San Jose. In Image Quality and System Performance VII, vol. 7529. Edited by: Farnand SP, Gaykema F. SPIE, Bellingham; 2010. doi:10.1117/12.839195
Chapelle O, Schòlkopf B, Zien A: Semi-Supervised Learning. MIT Press, Cambridge; 2006.
Acknowledgements
This work was partially supported by the NWO Veni grant 639.021.230.
Author information
Authors and Affiliations
Corresponding author
Additional information
Competing interests
The authors declare that they have no competing interests.
Authors’ original submitted files for images
Below are the links to the authors’ original submitted files for images.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License ( https://creativecommons.org/licenses/by/2.0 ), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Gastaldo, P., Zunino, R. & Redi, J. Supporting visual quality assessment with machine learning. J Image Video Proc 2013, 54 (2013). https://doi.org/10.1186/1687-5281-2013-54
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/1687-5281-2013-54

 , is a collection of data samples (patterns) holding N
p
input–output pairs (x
i
,y
i
).
, is a collection of data samples (patterns) holding N
p
input–output pairs (x
i
,y
i
).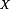 , is the space used to describe individual data items, e.g., x
, is the space used to describe individual data items, e.g., x 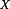 is the m-dimensional Euclidean space.
is the m-dimensional Euclidean space. , is the space of possible predictions; classification problems involve a binary setting y
, is the space of possible predictions; classification problems involve a binary setting y  and the output space
and the output space  .
. , is the set of functions that the learning algorithm examines to approximate the true function f.
, is the set of functions that the learning algorithm examines to approximate the true function f. , where
, where  is a feature space (i.e., the input space X, above):
is a feature space (i.e., the input space X, above):  , the media can be represented in a manner that is informative with respect to its visual quality. Quality assessment systems that process both the distorted signal and the original one are referred to as full reference (FR). Instead, reduced reference (RR) systems only require a limited set of numerical features extracted from the original signal, paying the (reasonable) additional cost of transmitting side information to the video chain endpoint. No reference (NR) systems assess perceived quality without any information on the original signal [
, the media can be represented in a manner that is informative with respect to its visual quality. Quality assessment systems that process both the distorted signal and the original one are referred to as full reference (FR). Instead, reduced reference (RR) systems only require a limited set of numerical features extracted from the original signal, paying the (reasonable) additional cost of transmitting side information to the video chain endpoint. No reference (NR) systems assess perceived quality without any information on the original signal [ , between the feature space
, between the feature space  and a scalar measure of the perceived quality, q
and a scalar measure of the perceived quality, q  :
:  )
)
 , and the criteria to evaluate the effectiveness of a hypothesis, h, at modeling f when processing input samples not included in
, and the criteria to evaluate the effectiveness of a hypothesis, h, at modeling f when processing input samples not included in 

 , attention should be paid to the process of data collection. This is even more important in visual quality assessment, where a time-consuming process needs to be completed to associate quality scores to visual stimuli; as a major consequence, available datasets usually include a limited number of input–output pairs.
, attention should be paid to the process of data collection. This is even more important in visual quality assessment, where a time-consuming process needs to be completed to associate quality scores to visual stimuli; as a major consequence, available datasets usually include a limited number of input–output pairs.