- Research Article
- Open access
- Published:
Three Novell Analog-Domain Algorithms for Motion Detection in Video Surveillance
EURASIP Journal on Image and Video Processing volume 2011, Article number: 698914 (2011)
Abstract
As to reduce processing load for video surveillance embedded systems, three low-level motion detection algorithms to be implemented on an analog CMOS image sensor are presented. Allowing on-chip segmentation of moving targets, these algorithms are both robust and compliant to various environments while being power efficient. They feature different trade-offs between detection performance and number of a priori choices. Detailed processing steps are presented for each of these algorithms and a comparative study is proposed with respect to some reference algorithms. Depending on the application, the best algorithm choice is then discussed.
1. Introduction
Motion detection in video surveillance with CMOS Image Sensors (CIS) requires high performance but it also needs to meet power consumption constraints, especially for remote sensing applications.
One way to address this issue is to design ASICs with specific image processing architectures. It allows some low level local analog processing to be performed at the sensor level (prior to A/D conversion), which is particularly power efficient. Thanks to submicron CMOS processes, the in-sensor processing can be performed without significantly impairing the device resolution and sensitivity. In the case of embedded video surveillance with a major concern on autonomy, such a physical motion detection implementation is a particularly interesting task to investigate since it allows extracting relevant information from a scene prior to broadcasting. This could be used to adapt the sensor's performance such as ADC resolution. Power consumption for capturing, storing, and transmitting the video would so be reduced. However, specific adapted algorithms have to be developed concurrently. Since such sensors have to be fully autonomous, these algorithms have to be both robust and compliant to various environments while being at the same time computationally and power efficient.
In the case of quasisteady camera (video still), adaptive environment modeling constitutes a key point in motion segmentation for surveillance systems. Among many works focusing on computer vision, the visual surveillance problem is discussed in [1], where conventional approaches for motion detection are presented. Implementation of optical flow measurement is also an interesting well-known technique in [2, 3]. These precedent approaches focus on optimizing motion detection in CIS but are not concerned with very low power image processing. In addition, optical flow methods based on Two-Frame Differential Method (i.e., Lucas and Kanade [4] or Horn and Schunk [5]) are based on hypotheses such as illumination steadiness. Such hypotheses are not always relevant, especially when objects move fast with respect to the frame rate. The aperture problem also constitutes a limitation to their straightforward implementation. Hence, these algorithms require iterative multiresolution processing as to extract information.
On the other hand, motion detection achieved by estimating background is based on weaker hypotheses. Background updating is an essential task since real-time algorithms for embedded systems have to be efficient in a large number of situations, that is able to adapt their sensitivity to the scene. Image segmentation with difference to background and adaptive threshold has been studied in [6], where the signal variance is computed from recursive average computations and then compared to a threshold obtained by averaging background variance over all the pixels. This method has been improved in [7] where its inherent trailing effect is compensated by a confidence weight representing the confidence of a pixel being part of the foreground. Adaptive threshold for motion detection in outdoor environment has been explored in [8]. The histogram of a distant matrix (obtained with Principal Component Analysis technique) and the variance of a mean image allow adapting the threshold level according to outdoor conditions. Other approaches based on multiple background estimations [9] or adaptive background estimation [10] have also been proposed.
All the precedent methods are efficient but require many operations. Due to the reduced processing resources available in CMOS Image Sensors, computational efficiency is so required yet keeping enough robustness. In order to perform low power motion detection in CIS, other methods based on background modeling have been proposed. In [11] low-level motion detection algorithms are presented and in [12], an efficient algorithm based on Σ-Δ modulation for artificial retinas is described. In this work, robustness improvement to false positives is achieved with local thresholding. For each pixel, background estimation and variance are computed with nonlinear operations to perform adaptive local thresholding.
In our proposed motion detection scheme for increased autonomy, such algorithms [11, 12] need to be improved in terms of false positives and detection efficiency while only using low power operations. The developed algorithms based on low-level computations are designed to be implemented on a versatile analog architecture allowing a wide range of operators and compact processing steps. In this paper, after a short presentation of our architectural choices and their consequences on the associated algorithms (part 2), we describe the motion detection algorithms we take as reference (part 3). We then present the developed motion detection algorithms with associated results and estimated power consumption (part 4). Finally, we discuss the algorithms performance from different points of view in order to balance purely simulated results according to targeted application.
2. Constraints and Targeted Architecture
2.1. Programmable Architecture
The considered programmable computational unit (Figure 1) is a low power SIMD machine based on analog processing [13]. It is composed of an  photosensors array to which an array of
photosensors array to which an array of  analog memory points (Analog RAM) is associated, where
analog memory points (Analog RAM) is associated, where  is the number of memory elements per pixel. In our implementation, we have chosen
is the number of memory elements per pixel. In our implementation, we have chosen  . Indeed, the analog memory is constrained by technological trade-offs such as silicon area and immunity to noise. The capacitive density is linked to technological parameters (with a typical value of 0.9 fF/μ m²). The temporal noise specifications of our architecture also impose a lower bound for capacitance value
. Indeed, the analog memory is constrained by technological trade-offs such as silicon area and immunity to noise. The capacitive density is linked to technological parameters (with a typical value of 0.9 fF/μ m²). The temporal noise specifications of our architecture also impose a lower bound for capacitance value  for a typical value of
for a typical value of  about 500 fF). According to these two parameters, 3 memory elements allow to keep reasonable memory area with regard to pixel matrix, while providing enough robustness with regard to noise and impact of parasitic capacitances.
about 500 fF). According to these two parameters, 3 memory elements allow to keep reasonable memory area with regard to pixel matrix, while providing enough robustness with regard to noise and impact of parasitic capacitances.  and
and  may be up to 1024. The so-formed matrix is bordered on one side by a vector of
may be up to 1024. The so-formed matrix is bordered on one side by a vector of  switched capacitor analog processors. A column of multiplexers selects the column of pixels or memories to be used by the processor. A sequencer, implemented by a digital IP CPU, delivers the successive processor instructions. For each processor instruction, the switches configurations for the OTA and for the associated analog registers are fixed. Hence, motion detection is directly performed on the pixel gray levels (voltage signals). The matrix does not embed Bayer filter. Thus, demosaicing is not required.
switched capacitor analog processors. A column of multiplexers selects the column of pixels or memories to be used by the processor. A sequencer, implemented by a digital IP CPU, delivers the successive processor instructions. For each processor instruction, the switches configurations for the OTA and for the associated analog registers are fixed. Hence, motion detection is directly performed on the pixel gray levels (voltage signals). The matrix does not embed Bayer filter. Thus, demosaicing is not required.
This architecture is implemented using a 0.35 μ m CMOS process. It features a 10 μ m pixel pitch with a standard fill factor (30%). With small parasitic capacitors and 3.3 V voltage swing, it constitutes a good compromise with respect to larger or to deep sub-micrometer processes. Moreover, leakages are also reduced compared to more advanced technologies, thus reducing static power consumption as well as defects in Analogue RAM (ARAM).
In order to take advantage of the SIMD architecture parallelism, the motion segmentation has to be performed independently for each pixel. The corresponding processing so requires many identical operations to be performed iteratively. Provided that the variables involved in the computations are independent, a parallel implementation of algorithms is thus possible and interesting in order to reduce the global power consumption. An analog-based computational system is an efficient response to these constraints.
With such an architecture, performing motion detection algorithms in the analog domain can be achieved with little power requirements. For example, mixing capacitors charges at pixel level [14] efficiently performs pixel averaging. A digital counterpart implementation would require numerous computations and power consuming data transfers.
The chosen programmable architecture globally enables the implementation of "simple" algorithms at a much reduced power cost. "Simple" is to be understood as stepwise linear algorithms based on a reduced temporal or spatial convolution kernel. From available basic operators, different low level algorithms can be implemented by suitably programming the architecture. The various operations required by our algorithms can be performed with this parallel architecture, relying on
-
(i)
pixel average,
-
(ii)
recursive average (i.e., weighted sums),
-
(iii)
fixed step increments/decrements,
-
(iv)
storage (state).
The most used operators are addition, multiplication of a variable by a fixed coefficient, increment, absolute value, and comparison. Conditional operations are needed, their executions depending upon comparison results referred to states.
Our analog-based architecture has been shown to overcome its digital counterparts in [15] in the context of a low power CMOS image sensor based on a waking up scheme for which the presented algorithms have been optimized.
2.2. Methodology
Concluding on algorithm performance is achieved by measuring motion detection performance on Matlab, as well as induced power consumption and temporal noise effect of CMOS devices using a SystemC model of the system (architecture and algorithm).
As to validate our algorithms performance, we have used different 8 bit sequences representative of indoor and outdoor conditions: Walk (IEF's sequence, rustling foliage), Pets 2002 (strobe light), dtneu_schnee (falling snow), and kwbB (i21http://www.ira.uka.de/), respectively (a), (b), (c), and (d) on Figure 2 and Hall Monitor (Figure 4). For instance, the falling snow in the dtneu_schnee sequence and the rustling foliage of Walk sequence both introduce parasitic changes of pixels' grey level and constitute realistic tests for the robustness of our algorithms. In our sequences, the objects to be detected are humans or cars.
2.3. Metrics Choice and Performance Evaluation
Performance metrics are based on [16]. During the simulation, motion segmentation is performed on gray level images resulting in binary images containing "moving" and "static" pixels. Each image is then divided in blocks of  pixels. If a block contains more than a predefined number of moving pixels, this block is then considered as a region of interest (ROI). From experimental evaluations based on a hand generated ground truth, an ROI can be considered as active when 5 to 10% of the pixels are "moving". Measurements for reference algorithms as well as proposed new ones are based on this value. For each frame, the state of each block is stored in a vector. This vector is compared to a reference which indicates ground truth information for the current frame. The number of True Positives and False Positives and Negatives can thus be counted (
pixels. If a block contains more than a predefined number of moving pixels, this block is then considered as a region of interest (ROI). From experimental evaluations based on a hand generated ground truth, an ROI can be considered as active when 5 to 10% of the pixels are "moving". Measurements for reference algorithms as well as proposed new ones are based on this value. For each frame, the state of each block is stored in a vector. This vector is compared to a reference which indicates ground truth information for the current frame. The number of True Positives and False Positives and Negatives can thus be counted ( ,
,  ,
,  ,
,  ).
).
Our considered performance criteria are
-
(i)
Detection Rate (
 ), which is the ability of the algorithm to detect moving objects,
), which is the ability of the algorithm to detect moving objects, -
(ii)
False Alarm Rate (
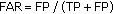 ) which estimates detection quality,
) which estimates detection quality, -
(iii)
False Positive Rate (
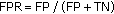 ), which is representative of algorithm robustness.
), which is representative of algorithm robustness.
In our sequence, nonrelevant motion concerns static elements of the scene or other elements such as snow in dtneu_schnee sequence, rustling foliage in Walk and kwbB sequences and strobe light in Pets 2002 sequence.
We have developed a faithful, Cycle Accurate, SystemC behavioral model of the architecture [17]. This model enables to jointly simulate the proposed algorithms and the processing architecture. This SystemC modeling is used to determine the number of instructions and the instruction rate required for each algorithm. The SystemC modeling also enables checking the consistency between the results obtained by the model and purely algorithmic results. A log file allows tracing instructions and data, hence enabling to check the whole coherence of the architecture for any conflicts during the parallel processing.
In order to take into account the impact of the nonidealities introduced by the analog parts and to get an accurate evaluation of power consumption, the analog blocks composing the architecture have been described at a low level, down to simple components like switches, capacitors, OTAs. For all these elementary blocks, relevant nonidealities have been modeled with respect to the target CMOS technology and validated thanks to classical electrical simulations (Spice-like). The power consumptions given in the next parts derive from this SystemC modeling of our architecture. Some hints about these aspects of the works have been exposed in [17].
3. Starting Point:  and
and 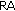 Algorithms
Algorithms
The embedded power motion detection algorithms have to meet two requirements: limited complexity, as to comply with our CIS computational limitations and high performance. In order to perform adaptive motion detection, background modeling has been chosen because of its computationally efficient implementation. In [11], two techniques allowing adaptive background modeling are presented. These algorithms perform local computations (i.e., from each pixel value) in order to generate low pass filtering on the observed scene. Approaches based on connected-component extraction, object merging, clustering are not explored here, because they require too intensive calculations with regard to the aimed architecture.
3.1. Background Estimation Using 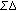 and Recursive Average Algorithms
and Recursive Average Algorithms
The autonomous remote CIS we develop must perform motion detection in unknown and potentially changing environments. In such configurations, algorithms must meet hard constraints of robustness and adaptability. Markovian algorithms are generally used to face these situations. However, with respect to the considered power consumption and computational constraints, we had to simplify algorithms of this class while preserving their robustness.
As reference algorithms, we consider the Recursive Average ( ) algorithm and the
) algorithm and the  algorithm, respectively, presented in [11, 12]. Both feature simple arithmetic computations. Moreover, the
algorithm, respectively, presented in [11, 12]. Both feature simple arithmetic computations. Moreover, the  algorithm, which follows the Markov model and has been used for real-time implementations in [18, 19], provides high robustness.
algorithm, which follows the Markov model and has been used for real-time implementations in [18, 19], provides high robustness.
3.1.1. Recursive Average: Principle
A first technique exposed in [11] relies on recursive operations. Considering a pixel value  (from 0 to 255), its background estimation
(from 0 to 255), its background estimation  is obtained from (1), with a large time constant fixed by
is obtained from (1), with a large time constant fixed by  .
.

As to evaluate the impact of time constants and other algorithm parameters, we plot the temporal variations of a pixel grey level along with its filtered output. The slower the to be detected object, the higher the required time constant. Figure 3 illustrates low pass filtering of a pixel signal using  . Not surprisingly from Figure 3, we can see that a proper choice of
. Not surprisingly from Figure 3, we can see that a proper choice of  , depending on frame rate, enables to extract background from moving objects. Yet this representation will help us explain the other algorithms. The visual impact of
, depending on frame rate, enables to extract background from moving objects. Yet this representation will help us explain the other algorithms. The visual impact of  is shown on Figure 4 showing estimated background with two different time constants.
is shown on Figure 4 showing estimated background with two different time constants.
Motion is then considered when the absolute difference between the estimated background and the processed pixel level is greater than a static global threshold (2).

This algorithm so performs basic motion detection while being well suited for our analog implementation. However, local thresholding must be considered to improve robustness. Motion detection performance is exposed on Table 1.
3.1.2.  : Principle
: Principle
The second method presented in [12] is based on nonlinear operations with Σ-Δ modulations. According to successive comparisons with signal value (3), a variable  is here incremented (4) or decremented (5) by a constant value so as to fit the pixel level
is here incremented (4) or decremented (5) by a constant value so as to fit the pixel level  .
.



As for  on Figure 3, Figure 5 illustrates low pass filtering of a pixel signal with
on Figure 3, Figure 5 illustrates low pass filtering of a pixel signal with  modulation method.
modulation method.
Considering an analogue implementation, the main advantage of this method is that it features more flexibility than the  algorithm. Indeed, estimated background variations can be adjusted by incrementation/decrementation steps, whereas time constant values of recursive averages are limited by the physical implementation of the computation. In our architecture, these time constant values are fixed by the ratios of the capacitances on which the signals charges are shared.
algorithm. Indeed, estimated background variations can be adjusted by incrementation/decrementation steps, whereas time constant values of recursive averages are limited by the physical implementation of the computation. In our architecture, these time constant values are fixed by the ratios of the capacitances on which the signals charges are shared.
Figure 6 shows the estimated background obtained with  modulations on the Hall Monitor sequence.
modulations on the Hall Monitor sequence.
For motion detection, based on the same modulations than (4) or (5), a variable  is generated. It can be interpreted as the signal variance and allows to threshold the absolute difference
is generated. It can be interpreted as the signal variance and allows to threshold the absolute difference  between the pixel signal
between the pixel signal  and the estimated background
and the estimated background  (Figure 7). Motion is detected when
(Figure 7). Motion is detected when  is higher than
is higher than  .
.

Instead of the global threshold used in  , the
, the  algorithm so computes a local adaptive threshold for each pixel as to achieve more robustness on noisy elements, while keeping enough sensitivity on static background. Thanks to the observed scene nonuniformity, local thresholding is computed according to the temporal activity of each zone. Moreover, this algorithm features no trailing effects, at the cost of a poor band pass filtering capability.
algorithm so computes a local adaptive threshold for each pixel as to achieve more robustness on noisy elements, while keeping enough sensitivity on static background. Thanks to the observed scene nonuniformity, local thresholding is computed according to the temporal activity of each zone. Moreover, this algorithm features no trailing effects, at the cost of a poor band pass filtering capability.
3.1.3. Recursive Average and  Performance
Performance
Table 1 presents the motion performance of state-of-the-art algorithms. The  value used for the
value used for the  algorithm is 25. The
algorithm is 25. The  value used for the
value used for the  algorithm (required for threshold processing) is 15.
algorithm (required for threshold processing) is 15.
 exhibits poor robustness. Indeed, this algorithm requires setting a global threshold that constitutes the main limitation of this method since no sensitivity adaptation according to scene activity can be performed. Moreover,
exhibits poor robustness. Indeed, this algorithm requires setting a global threshold that constitutes the main limitation of this method since no sensitivity adaptation according to scene activity can be performed. Moreover,  exhibits phase shifting resulting in trailing effects and poor band pass filtering. More specifically, this algorithm does not allow high frequency rejection along with background subtraction.
exhibits phase shifting resulting in trailing effects and poor band pass filtering. More specifically, this algorithm does not allow high frequency rejection along with background subtraction.
The motion detection performance exposed for the  algorithm clearly shows the interest of local adaptive thresholding compared to the global one used by the
algorithm clearly shows the interest of local adaptive thresholding compared to the global one used by the  algorithm.
algorithm.
However, the on-chip motion detection information can be used to adapt the sensor performance (e.g., higher ADC accuracy on moving pixels). In order to keep a reasonable global power consumption (a few mW), an improved robustness of these on-chip motion detection analog domain algorithms is still required while keeping high detection rate.
4. Algorithms
We now describe our three designed motion segmentation algorithms for CIS:
-
(i)
a first algorithm running with no a priori determination of constant, based on scene activity to adapt its sensitivity,
-
(ii)
a second algorithm using band pass filtering in order to reduce false positives upon high frequency pixel variations,
-
(iii)
finally, an algorithm featuring only one constant to determine a priori, and reducing the trailing effect induced by recursive averaging.
4.1. Scene-Based Adaptive Algorithm (SBA)
In order to improve adaptability, we now present the Scene-Based Adaptive (SBA) algorithm. This algorithm derives from the  algorithm in [12]. It performs motion segmentation on gray level sequences with no a priori constant determination, like the N constant used in
algorithm in [12]. It performs motion segmentation on gray level sequences with no a priori constant determination, like the N constant used in  . Based on
. Based on  modulations, the SBA algorithm is also compliant with the reduced available computational resources of CIS architectures, thus eliminating true Markovian approaches.
modulations, the SBA algorithm is also compliant with the reduced available computational resources of CIS architectures, thus eliminating true Markovian approaches.
Our idea is to get rid of constants related to the background of the scene. The detection of grey level variations resulting from motion derives from the absolute difference  between the last extremum and the current pixel value
between the last extremum and the current pixel value  (Figure 8). Instead of detecting grey level variations like in (4) and (5), this filter requires no constant setting.
(Figure 8). Instead of detecting grey level variations like in (4) and (5), this filter requires no constant setting.
The  value generated is now used to perform adaptive motion detection with the technique presented below.
value generated is now used to perform adaptive motion detection with the technique presented below.
First, the mean value  of
of  is computed (7). Considering that insignificant motions of the background introduce only small variations changes, the idea is to favor large signal variations at the expense of small ones. A convex function is so needed to amplify
is computed (7). Considering that insignificant motions of the background introduce only small variations changes, the idea is to favor large signal variations at the expense of small ones. A convex function is so needed to amplify  . Therefore, (8) introduces
. Therefore, (8) introduces  which is an approximation of
which is an approximation of  . Indeed, our switched capacitor architecture enables only multiplication between a digital number (i.e., the steps of
. Indeed, our switched capacitor architecture enables only multiplication between a digital number (i.e., the steps of  ) and an analog value (i.e.,
) and an analog value (i.e.,  ).
).
In order to reduce the trailing effects, the next step consists in building an adjustable increment, much like in adaptive  . A third variable
. A third variable  is thus obtained from the signal value (9). Indeed,
is thus obtained from the signal value (9). Indeed,  derives from a
derives from a  modulation of the signal value using an increment equal to
modulation of the signal value using an increment equal to  . If the absolute difference between
. If the absolute difference between  and
and  is larger than
is larger than  (10), then the pixel variation is reckoned as relevant and motion is detected.
(10), then the pixel variation is reckoned as relevant and motion is detected.




The absolute difference between  and
and  can be seen as the maximal estimated signal dispersion. A larger variation than the estimated one is considered due to a relevant moving object (10). Apart from the increment or decrement level, this algorithm runs without any a priori fixed constant.
can be seen as the maximal estimated signal dispersion. A larger variation than the estimated one is considered due to a relevant moving object (10). Apart from the increment or decrement level, this algorithm runs without any a priori fixed constant.
Figure 9 illustrates SBA computations of a pixel signal. In absence of motion, one can notice that  fits
fits  (
( ). Compared to
). Compared to  , the estimator of the background can have a steeper slope when large signal variations occur. Reciprocally, small changes of the pixel grey level lead to long time constants.
, the estimator of the background can have a steeper slope when large signal variations occur. Reciprocally, small changes of the pixel grey level lead to long time constants.
Figure 10 illustrates motion detection performed with the  and SBA algorithms. In the presented algorithm, some trailing effect can be observed but with a better robustness: in this illustration, the rustling foliage is filtered while motion detection is preserved on the pedestrian.
and SBA algorithms. In the presented algorithm, some trailing effect can be observed but with a better robustness: in this illustration, the rustling foliage is filtered while motion detection is preserved on the pedestrian.
4.2. Recursive Average with Estimator Algorithm (RAE)
In various outdoor situations, many false alarm sources can be encountered. Despite the fact that the static background encountered in urban area does not provide such constraints, weather conditions in the same areas can lead to increased FPR and FAR. In [12], no high frequency rejection is performed, thus implying numerous false positives.
Figure 12(b) illustrates motion detection, performed at a crossroad under falling snow, with the  algorithm. In order to improve motion detection robustness by rejecting high frequency variations, we have designed an algorithm featuring band pass filtering. It is also based on recursive average which can be compactly implemented considering charge transfer between capacitances. Though having the same degree of complexity, the designed algorithm is thus optimized for an analog-based architecture, compared to delta modulation.
algorithm. In order to improve motion detection robustness by rejecting high frequency variations, we have designed an algorithm featuring band pass filtering. It is also based on recursive average which can be compactly implemented considering charge transfer between capacitances. Though having the same degree of complexity, the designed algorithm is thus optimized for an analog-based architecture, compared to delta modulation.
4.3. Recursive Average with Estimator Algorithm (RAE)
In various outdoor situations, many false alarm sources can be encountered. Despite the fact that the static background encountered in urban area does not provide such constraints, weather conditions in the same areas can lead to increased FPR and FAR. In [12], no high frequency rejection is performed, thus implying numerous false positives.
Figure 12(b) illustrates motion detection, performed at a crossroad under falling snow, with the  algorithm. In order to improve motion detection robustness by rejecting high frequency variations, we have designed an algorithm featuring band pass filtering. It is also based on recursive average which can be compactly implemented considering charge transfer between capacitances. Though having the same degree of complexity, the designed algorithm is thus optimized for an analog-based architecture, compared to delta modulation.
algorithm. In order to improve motion detection robustness by rejecting high frequency variations, we have designed an algorithm featuring band pass filtering. It is also based on recursive average which can be compactly implemented considering charge transfer between capacitances. Though having the same degree of complexity, the designed algorithm is thus optimized for an analog-based architecture, compared to delta modulation.
This algorithm is thus based on a background estimation extracted from the difference between two low pass filters. The computation of two recursive averages ( (12) and
(12) and  (13)), each with its own time constant (fixed by the
(13)), each with its own time constant (fixed by the  and
and  parameters), allows here to define a band pass filter: the slowest is used to bring out the background while the other, with short lag, filters out the signal's fast perturbations. For each pixel, the main computation steps are described below.
parameters), allows here to define a band pass filter: the slowest is used to bring out the background while the other, with short lag, filters out the signal's fast perturbations. For each pixel, the main computation steps are described below.  represents the frame index,
represents the frame index,  the current gray level value for the considered block, and
the current gray level value for the considered block, and  a local threshold (14).
a local threshold (14).




An adaptive threshold based on the temporal variations of this absolute difference allows detecting motion. If this estimator  becomes larger than a local threshold
becomes larger than a local threshold  , which depends on the
, which depends on the  temporal activity, motion is detected.
temporal activity, motion is detected.  acts as a band-pass filter selecting only moving objects of interest in the scene. The adaptive threshold is obtained by using
acts as a band-pass filter selecting only moving objects of interest in the scene. The adaptive threshold is obtained by using  ,
the recursive average of
,
the recursive average of  ,
as a variable amplifying gain for the threshold (17). The increase of the threshold level
,
as a variable amplifying gain for the threshold (17). The increase of the threshold level  , due to signal variations, can be seen on Figure 11. With this method,
, due to signal variations, can be seen on Figure 11. With this method,  directly depends on
directly depends on  perturbation level, periodicity or persistence. To prevent saturation (considering either analog or fixed point implementation),
perturbation level, periodicity or persistence. To prevent saturation (considering either analog or fixed point implementation),  is amplified rather than
is amplified rather than  . The time constant of this threshold must be quite large with respect to pertinent scene motions in order to adapt the sensitivity to persistent perturbations only.
. The time constant of this threshold must be quite large with respect to pertinent scene motions in order to adapt the sensitivity to persistent perturbations only.
These recursive operations with few memory requirements make this algorithm easy to implement on our architecture. The time constant for fast recursive average can be determined in order to allow an efficient fast perturbations filtering while not inducing significant trail effect. Considering the  -transform of the recursive average, the time constant is given as follows:
-transform of the recursive average, the time constant is given as follows:

The response to a step function with amplitude  of the transfer function defined by
of the transfer function defined by  is expressed in (16), with
is expressed in (16), with  and
and  being the constants used in (12) and (13).
being the constants used in (12) and (13).

In this algorithm, the two constants ( ) depend on the to-be detected objects properties (i.e., size and speed) and on the frame rate. However, knowing the type of object to be detected, local adaptive thresholding is achieved. In the following section, these (
) depend on the to-be detected objects properties (i.e., size and speed) and on the frame rate. However, knowing the type of object to be detected, local adaptive thresholding is achieved. In the following section, these ( ) constants have been, respectively, set to (22, 24) for the simulations performed on the reference sequences, with a 25 Hz frame rate. The class of objects to detect here are cars or pedestrians. The power of two based sizing for
) constants have been, respectively, set to (22, 24) for the simulations performed on the reference sequences, with a 25 Hz frame rate. The class of objects to detect here are cars or pedestrians. The power of two based sizing for  and
and  facilitates our analog implementation with regard to component matching. With
facilitates our analog implementation with regard to component matching. With  , the 95% rise time is
, the 95% rise time is  which corresponds approximately to 50 frames at 25 fps. Considering tested videos, this value has experimentally shown efficient background estimation. Choosing
which corresponds approximately to 50 frames at 25 fps. Considering tested videos, this value has experimentally shown efficient background estimation. Choosing  is a good compromise between implementation constraints and filtering efficiency (in order not to reduce DR, while improving FAR).
is a good compromise between implementation constraints and filtering efficiency (in order not to reduce DR, while improving FAR).

The constant  has been set to 26 (
has been set to 26 ( or 200 frames). The
or 200 frames). The  constant can be typically set around 2 and can be increased in order to reduce false positives.
constant can be typically set around 2 and can be increased in order to reduce false positives.
Figure 11 illustrates computations of a pixel signal using the proposed algorithm.
One can notice that this algorithm can bring efficient filtering of high frequency perturbations. However, some trailing effect is observed with the RAE algorithm (not obtained with  ). Figure 12 illustrates RAE applied on the dtneu_schnee sequence with falling snow. With the same sensitivity as
). Figure 12 illustrates RAE applied on the dtneu_schnee sequence with falling snow. With the same sensitivity as  , this algorithm allows to filter these high frequency perturbations.
, this algorithm allows to filter these high frequency perturbations.
4.4. Adaptive Wrapping Thresholding Algorithm (AWT)
Although being robust and computationally efficient, the  and RAE algorithms require determining some constants. According to the known frame rate, the
and RAE algorithms require determining some constants. According to the known frame rate, the  ,
, , and
, and constants of RAE as well as the increment level of
constants of RAE as well as the increment level of  can be determined a priori. However, the RAE
can be determined a priori. However, the RAE  constant or the
constant or the  constant allows adjusting the algorithm sensitivity in accordance with the amplitude of noisy elements. In order to avoid defining a priori constants, an Adaptive Wrapping Thresholding motion detection algorithm (AWT), based on recursive average operations with a reduced number of constants, is presented in this section. Unlike common algorithms based on recursive low pass filtering [6], this algorithm also limits the trailing effect due to phase shifting.
constant allows adjusting the algorithm sensitivity in accordance with the amplitude of noisy elements. In order to avoid defining a priori constants, an Adaptive Wrapping Thresholding motion detection algorithm (AWT), based on recursive average operations with a reduced number of constants, is presented in this section. Unlike common algorithms based on recursive low pass filtering [6], this algorithm also limits the trailing effect due to phase shifting.
We thus propose an algorithm based on recursive average operations performing local adaptive thresholding from each pixel signal (Figure 13). In the two precedent algorithms (SBA and RAE), motion detection is performed by thresholding temporal variations ( ). We propose here to compute two wrapping variables in order to detect significant variations of the signal. These two variables are used to define the upper and lower bounds between which the grey level of the signal should remains. In order to take into account the variations of the background, those two variables are updated using a low pass-filter. Yet the time constant of these filters can be much larger than the ones used in
). We propose here to compute two wrapping variables in order to detect significant variations of the signal. These two variables are used to define the upper and lower bounds between which the grey level of the signal should remains. In order to take into account the variations of the background, those two variables are updated using a low pass-filter. Yet the time constant of these filters can be much larger than the ones used in  and even SBA.
and even SBA.
This algorithm relies on a background estimation for each pixel signal from which we estimate the signal standard deviation. This standard deviation is then used to estimate a maximum range for background variations. If the value of a considered pixel moves outside this estimated range of background variations, we consider that motion occurs.
First of all, background estimation ( ) is computed recursively (19). The temporal variations (
) is computed recursively (19). The temporal variations ( ) are extracted as absolute difference between the pixel signal (
) are extracted as absolute difference between the pixel signal ( ) and the background estimation (20). The mean deviation of the estimated background variations (
) and the background estimation (20). The mean deviation of the estimated background variations ( ) is then calculated from (
) is then calculated from ( ) (21). In a fourth step, two variables (
) (21). In a fourth step, two variables ( and
and  ) are computed (22) and (23), which allow here to define the estimated range of maximum background variations. Motion is then considered according to (24).
) are computed (22) and (23), which allow here to define the estimated range of maximum background variations. Motion is then considered according to (24).







Hence this algorithm relies on a constant,  , allowing to determine the time constant of recursive averages (equivalent to increment/decrement levels of the
, allowing to determine the time constant of recursive averages (equivalent to increment/decrement levels of the  algorithm [12]). However, no additional constant is required to handle sensitivity, unlike
algorithm [12]). However, no additional constant is required to handle sensitivity, unlike  or RAE where a coefficient is required to set the threshold level. Computations of
or RAE where a coefficient is required to set the threshold level. Computations of  and
and  allow here to define adaptive thresholding directly from the signal variations (Figure 13).
allow here to define adaptive thresholding directly from the signal variations (Figure 13).
Furthermore, this method allows reducing the trailing effect observed with common motion detection algorithms based on recursive average. Indeed, recursive average based on signal level induces phase shifting and trail effect on target. With this algorithm, the double condition in motion detection with  and
and  reduces the trailing effect (Figure 14).
reduces the trailing effect (Figure 14).
Unlike  , SBA or RAE, there is no need for a multiplication operation. From our analog implementation point of view, this constitutes an improvement since there is no need to implement multiple capacitors to get a wide range of constants for multiplication.
, SBA or RAE, there is no need for a multiplication operation. From our analog implementation point of view, this constitutes an improvement since there is no need to implement multiple capacitors to get a wide range of constants for multiplication.
5. Results
5.1. Algorithms Performance
Table 2 exposes the different results of the state-of-the-art algorithms ( and
and  ), as well as new ones (SBA, RAE, and AWT).
), as well as new ones (SBA, RAE, and AWT).
Simulations performed on sequences with the SBA algorithm without any arbitrary constant (Table 3) provides quite similar detection rate along with close FAR and FPR measurements, compared to  measurements (Table 2). This algorithm thus provides equivalent detection efficiency and robustness, with no need for constant settling, thus showing improved adaptability. Although it does not feature a high frequency rejection, a satisfying detection performance is achieved on gray level sequences.
measurements (Table 2). This algorithm thus provides equivalent detection efficiency and robustness, with no need for constant settling, thus showing improved adaptability. Although it does not feature a high frequency rejection, a satisfying detection performance is achieved on gray level sequences.
The results exposed on Table 4 show that RAE is equivalent to  in terms of DR for all sequences. However, better results are obtained by our algorithm with respect to FPR and FAR. This algorithm so features different variables allowing motion segmentation on gray level sequences with a good sensitivity and high frequency rejection. However, a constant k allowing threshold setting is required and some trailing effect is generated.
in terms of DR for all sequences. However, better results are obtained by our algorithm with respect to FPR and FAR. This algorithm so features different variables allowing motion segmentation on gray level sequences with a good sensitivity and high frequency rejection. However, a constant k allowing threshold setting is required and some trailing effect is generated.
The AWT algorithm results are slightly below the performance levels of RAE. However, no a priori choice of threshold sensitivity has been made. Hence these results highlight interesting performance about motion detection without environment knowledge.
TheWalk sequence denotes reduced robustness here. Although rustling foliage is efficiently filtered out by our algorithms, the motion of the tree branches has the same speed and amplitude characteristics as the objects to be detected (e.g., humans). The single processing is not robust to such motion.
The power consumption is proportional to the Number of Instructions (NOI). From SystemC simulations applied to  30 fps video sequences, we have estimated a power consumption below 5 mW for the worst case (SBA algorithm). This is less than the power consumption of a state of the art 3 M samples/s 10-bit Successive Approximation Register (SAR) ADC designed in the same technology, that is between 10 and 20 mW. The SAR are known to be the least power consuming ADC architectures. This validates the relevance of the algorithm architecture codesign since a digital implementation of those algorithms would require such an ADC plus a digital processing unit. Furthermore, our analog processing unit derives from a SAR ADC; therefore, the scaling of the CMOS technology brings the same improvements as for the classical SAR ADC.
30 fps video sequences, we have estimated a power consumption below 5 mW for the worst case (SBA algorithm). This is less than the power consumption of a state of the art 3 M samples/s 10-bit Successive Approximation Register (SAR) ADC designed in the same technology, that is between 10 and 20 mW. The SAR are known to be the least power consuming ADC architectures. This validates the relevance of the algorithm architecture codesign since a digital implementation of those algorithms would require such an ADC plus a digital processing unit. Furthermore, our analog processing unit derives from a SAR ADC; therefore, the scaling of the CMOS technology brings the same improvements as for the classical SAR ADC.
So as to take into account technological parameters in these simulations, temporal noise had been added in these sequences via our SystemC model. Indeed, in our architecture, several noise sources create signal variations that can be interpreted as relevant motion. In our model, the 8-bit images are converted into voltage signal on a 1.8 V dynamic range. An additional Gaussian noise with a 1.1 mV standard deviation is added to each image. During processing, a second Gaussian noise source with a 0.25 mV standard deviation is added to each operation to model analog processor nonidealities.
Table 3 presents the impact of noise on analog processing on the different motion detection parameters considered.
We can see that in the case of SBA and  , DR is reduced while FAR is increased. For these two algorithms, noise induces less sensitivity on relevant part of the scene, while decreasing global robustness. These results highlight the lower robustness of these two algorithms when implemented in our analog architecture. Concerning the RAE algorithm, both DR and FAR are amplified. This can be due to an insufficient threshold amplification. For AWT algorithm, the whole parameters are decreased. The threshold amplification is too high for this one, leading to less sensitivity on the whole images. However, the noise added on recursive average-based processing (RAE, AWT) induces fewer variations for the selected parameters. Thus we can consider that the recursive average-based methods are more robust than the ones based on
, DR is reduced while FAR is increased. For these two algorithms, noise induces less sensitivity on relevant part of the scene, while decreasing global robustness. These results highlight the lower robustness of these two algorithms when implemented in our analog architecture. Concerning the RAE algorithm, both DR and FAR are amplified. This can be due to an insufficient threshold amplification. For AWT algorithm, the whole parameters are decreased. The threshold amplification is too high for this one, leading to less sensitivity on the whole images. However, the noise added on recursive average-based processing (RAE, AWT) induces fewer variations for the selected parameters. Thus we can consider that the recursive average-based methods are more robust than the ones based on  modulations (
modulations ( , SBA), when implemented in our analog architecture.
, SBA), when implemented in our analog architecture.
5.2. Discussion
In the precedent part, we have presented 3 robust and fast new algorithms and compared them to the reference  algorithm. Based on particular parameters allowing the measurement of motion detection performance, such as detection rate or false positive rate, we have determined the robustness or detection efficiency of these algorithms. The average results for the tested sequences are presented on Table 4.
algorithm. Based on particular parameters allowing the measurement of motion detection performance, such as detection rate or false positive rate, we have determined the robustness or detection efficiency of these algorithms. The average results for the tested sequences are presented on Table 4.
However, these results must be balanced by some factors. Indeed, we can define some criteria allowing taking into account implementation constraints such as power consumption or other limitations like the kind of targeted application for motion detection algorithm. We have exposed below some of the criteria, which can be found according to motion detection context. Table 5 illustrates the rates of each algorithm according to these criteria.
-
(1)
settings: the fewer the required constants for adapting threshold level or time constants, the more autonomous the left-behind sensor,
-
(2)
adaptation: threshold level evolution according to pixel temporal activity,
-
(3)
high frequency rejection: high frequency noise filtering of pixel signal (band pass filtering),
-
(4)
trailing effect: artefacts or motion segmentation distortion due to phase shifting induced by algorithm,
-
(5)
robustness: number of generated false positives,
-
(6)
computational efficiency: induced power consumption (mainly depending on the number of instructions in our implementation),
-
(7)
robustness with regard to analog implementation (temporal noise).
These qualitative results show that, depending on the aimed application, an algorithm can prevail on another, even if its motion detection performance is worse. However, AWT and RAE are better suited for an analog implementation.
6. Conclusion
Three algorithms developed using a codesign approach have been presented. They perform motion detection at reduced power consumption while ensuring fast and robust computation. Compared to classical sensors performing motion detection downstream the image acquisition, the offered processing capabilities are somehow limited, but the chosen analog architecture, on which they are implemented, offers a better compromise between power consumption and algorithm performance. Moreover, considering only the algorithmic aspect of the works, significant improvements have been brought in terms of self-adaptability to the scene. Constants involved in the presented algorithms are indeed mostly depending on the nature of the objects to be detected (speed and size).
Though these algorithms have been tailored for a dedicated architecture, a real-time implementation on a standard digital processor (e.g., an ARM920T) is however possible but at a significantly higher power consumption (roughly some 100 mW for the processor alone).
Finally, an ASIC is currently being designed as to provide an experimental validation of the concept. One of its main features is that the pixel area ( μ m2) is very close to state-of-the-art pixels in similar technology (0.35 μ m CMOS).
μ m2) is very close to state-of-the-art pixels in similar technology (0.35 μ m CMOS).
References
Hu W, Tan T, Wang L, Maybank S: A survey on visual surveillance of object motion and behaviors. IEEE Transactions on Systems, Man and Cybernetics Part C 2004, 34(3):334-352. 10.1109/TSMCC.2004.829274
Moini A, Bouzerdoum A, Eshraghian K, Yakovleff A, Nguyen XT, Blanksby A, Beare R, Abbott D, Bogner RE: An insect vision-based motion detection chip. IEEE Journal of Solid-State Circuits 1997, 32(2):279-284. 10.1109/4.551924
Mehta S, Etienne-Cummings R: Normal optical flow measurement on a CMOS APS imager. Proceedings of the IEEE International Symposium on Cirquits and Systems (ISCAS '04), May 2004 4: 848-851.
Lucas BD, Kanade T: An iterative image registration technique with an application to stereo vision. Proceedings of the 7th International Joint Conference on Artificial Intelligence (IJCAI '81), April 1981 674-679.
Horn BKP, Schunck BG: Determining optical flow. Artificial Intelligence 1981, 17(1-3):185-203. 10.1016/0004-3702(81)90024-2
Joo S, Zheng Q: A temporal variance-based moving target detector. Proceedings of the IEEE Workshop on Performance Analysis of Video Surveillance and Tracking (PETS '05), January 2005
Abdelkader MF, Chellappa R, Zheng Q, Chan AL: Integrated motion detection and tracking for visual surveillance. Proceedings of the 4th IEEE International Conference on Computer Vision Systems (ICVS '06), January 2006 28.
Vázquez JF, Mazo M, Lázaro JL, Luna CA, Ureña J, Garcia JJ, Guillan E: Adaptive threshold for motion detection in outdoor environment using computer vision. Proceedings of the IEEE International Symposium on Industrial Electronics (ISIE '05), June 2005 3: 1233-1237.
Pan W, Wu K, Chai Z, You ZS: A background reconstruction method based on double-background. Proceedings of the 4th International Conference on Image and Graphics (ICIG '07), August 2007 502-507.
Guo J, Rajan D, Chng ES: Motion detection with adaptive background and dynamic thresholds. Proceedings of the 5th International Conference on Information, Communications and Signal Processing, December 2005 41-45.
Richefeu J, Manzanera A: Motion detection with smart sensor. Proceedings of the 9th Congress Young Searchers in Computer Vision (ORASIS '05), May 2005
Manzanera A, Richefeu JC: A new motion detection algorithm based on Σ-Δ background estimation. Pattern Recognition Letters 2007, 28(3):320-328. 10.1016/j.patrec.2006.04.007
Moutault S, Mathias H, Klein JO, Dupret A: An improved analog computation cell for Paris II, a programmable vision chip. Proceedings of the IEEE International Symposium on Cirquits and Systems (ISCAS '04), May 2004 453-456.
Massie M, Baxter C, Curzan JP, McCarley P, Etienne-Cummings R: Vision chip for navigating and controlling micro unmanned aerial vehicles. Proceedings of IEEE International Symposium on Circuits and Systems (ISCAS '03), May 2003 3: 786-789.
Verdant A, Dupret A, Mathias H, Villard P, Lacassagne L: Adaptive multiresolution for low power CMOS image sensor. Proceedings of the 14th IEEE International Conference on Image Processing (ICIP '06), September-October 2007, San Antonio, Tex, USA 5: 185-188.
Black J, Ellis TJ, Rosin P: A novel method for video tracking performance evaluation. Proceedings of the IEEE Workshop on Performance Analysis of Video Surveillance and Tracking (PETS '03), October 2003 125-132.
Verdant A, Villard P, Dupret A, Mathias H: SystemC validation of a low power analog CMOS image sensor architecture. Proceedings of the IEEE North-East Workshop on Circuits and Systems (NEWCAS '07), August 2007 903-906.
Lacassagne L, Milgram M, Garda P: Motion detection, labeling, data association and tracking, in real-time on RISC computer. Proceedings of International Conference on Image Analysis and Processing (ICIP '99), 1999, Venice, Italy 520-525.
Denoulet J, Mostafaoui G, Lacassagne L, Mérigot A: Implementing motion Markov detection on general purpose processor and associative mesh. Proceedings of the 7th International Workshop on Computer Architecture for Machine Perception (CAMP '05), July 2005, Palermo, Italy 288-293.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License ( https://creativecommons.org/licenses/by/2.0 ), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Verdant, A., Villard, P., Dupret, A. et al. Three Novell Analog-Domain Algorithms for Motion Detection in Video Surveillance. J Image Video Proc. 2011, 698914 (2011). https://doi.org/10.1155/2011/698914
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1155/2011/698914


 ), which is the ability of the algorithm to detect moving objects,
), which is the ability of the algorithm to detect moving objects,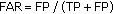 ) which estimates detection quality,
) which estimates detection quality,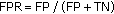 ), which is representative of algorithm robustness.
), which is representative of algorithm robustness. and
and 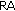 Algorithms
Algorithms and Recursive Average Algorithms
and Recursive Average Algorithms
 ) with recursive average filtering for a temporal pixel variation (
) with recursive average filtering for a temporal pixel variation ( ) as a function of time.
) as a function of time.
 : Principle
: Principle
 modulation.
modulation. is the pixel gray level value,
is the pixel gray level value,  is the estimation of the background as a function of time.
is the estimation of the background as a function of time.

 algorithm.
algorithm. the threshold of
the threshold of  .
. Performance
Performance

 and
and  as, respectively, expressed in (8) and (9).
as, respectively, expressed in (8) and (9).
 , and(c) Motion detection with SBA.
, and(c) Motion detection with SBA.

 is the pixel gray level value with the variables
is the pixel gray level value with the variables  ,
,  ,
,  , and
, and  as, respectively, expressed in (12), (13), (14), and (17).
as, respectively, expressed in (12), (13), (14), and (17).
 algorithm (
algorithm (
 ) (b) and the RAE algorithm (c).
) (b) and the RAE algorithm (c).

 is the pixel gray level value, with the variables
is the pixel gray level value, with the variables  ,
,  ,
,  ,
,  , and
, and  as, respectively, expressed in (19), (21), (22), (23), and (20).
as, respectively, expressed in (19), (21), (22), (23), and (20).