- Research Article
- Open access
- Published:
Chroma Noise Reduction in DCT Domain Using Soft-Thresholding
EURASIP Journal on Image and Video Processing volume 2010, Article number: 323180 (2011)
Abstract
The chroma noise effect seriously reduces the quality of digital images and videos, especially if they are acquired in low-light conditions. This paper describes the DCT-CNR (Discrete Cosine Transform-Chroma Noise Reduction), an efficient chroma noise reduction algorithm based on soft-thresholding. It reduces the contribution of the DCT coefficients having highest probability to be corrupted by noise and preserves the ones corresponding to the details of the image. Experiments show that the proposed method achieves good results with low computational and hardware resources requirements.
1. Introduction
Noise is one of the most critical problems in digital images, especially in low-light conditions. The relative amount of "chroma" and "luminance" noise varies depending on the exposure settings and on the camera model. In particular, low-light no-flash photography suffers from severe noise problems. A complete elimination of luminance noise can be unnatural and the full chroma noise removal can introduce false colors; so the denoising algorithms should vary properly the filtering strength, depending on the input local characteristics.
In literature there are several techniques for chroma noise reduction. Some of them make use of optical filters installed in the digital cameras to avoid aliasing [1–3]. Other approaches manage the high frequencies only and are ineffective against low-frequency chroma noise.
Another common and simple way to address the problem consists of converting the input image to luminance-chrominance space, blurring the chroma planes and transforming the image back to the original color domain [4]. The main weakness of this technique is the inability to discern between noise and genuine color details; so, when the blurring becomes strong, color bleeding along edges can be introduced. Moreover, large blurring kernels are needed to remove low-frequencies chroma blobs. Another fast solution consists of applying standard greyscale image algorithms to each color plane of the input image independently, but the risk of artefacts or false colors introduction is very high because the correlation among color channels is ignored [5].
The solution proposed by Kodak [6] promises to overcome the limitation of the methods described above. The basic idea behind the algorithm is to identify the edges of the input image and to use variable shaped blur kernels to reduce the noise. This strategy allows managing low-frequencies blobs and avoiding color bleeding. It can be summarized in four steps. The input image is firstly converted to the CIELAB [7] color space. An edge map is then built convolving four 5 × 5 truncated pyramid filters [8] with luminance and chrominance channels and summing the results to obtain a single edge map. Then four filters capture high frequencies corresponding to horizontal, vertical, and diagonals edges. The chrominance channels are smoothed to remove noise. For each pixel of the image, the corresponding edge map value is taken as reference. Then the algorithm moves in each of the eight preferred directions (North, North-East, East, South-East, South, South-West, West, North-West), one pixel at a time, comparing the edge map values with the reference value. If the difference between the current and the reference values is lower than a threshold, the current pixel is added to the smoothing neighbourhood region and the process continues; otherwise the growth of the region along the current direction is stopped. When the blur kernel shape is computed, the chrominance values are replaced with the average of the neighbouring pixels falling in the kernel. The threshold can be fixed by the user or computed adaptively in run-time, for example, by calculating the standard deviation of the edges map values in a flat region of the image. The final step consists of converting the resulting image back to the original color space.
Another classic and well-known approach consists of removing noise by considering a proper domain transform (Figure 1). The basic idea is to perform a soft or hard thresholding [9] on the wavelet [10] or on Discrete Cosine Transform (DCT) coefficients [11]. The wavelet transform decomposes the signal into low-frequencies and high-frequencies subbands. Since most of the image information is concentrated in a few coefficients, the high-frequencies subbands are processed with hard- or soft-thresholding operations. Several strategies have been proposed to solve the critical problem of threshold selection [12–14] and one more approach based on fuzzy logic is presented in this paper. A recent alternative technique is the bilateral filter [15]. The bilateral filter takes a weighted sum of the pixels in a local neighbourhood; the weights depend on both the spatial and the intensity distances and are tuned to preserve edges and reduce noise. Mathematically, for every pixel  , the output of the bilateral filter is calculated as follows:
, the output of the bilateral filter is calculated as follows:

where  and
and  are parameters controlling the fall-off of the weights, respectively, in spatial and intensity domains,
are parameters controlling the fall-off of the weights, respectively, in spatial and intensity domains,  is a spatial neighbourhood of
is a spatial neighbourhood of  , and
, and  is the normalization constant defined as follows:
is the normalization constant defined as follows:

The multiresolution bilateral filtering and the wavelet threshold are then combined to provide a new and effective chroma noise reduction framework in [16], where an empirical study of optimal bilateral filter parameters selection is provided.
Chroma noise reduction has application in astrophotography too. PixInsight [17] is an advanced image processing platform produced by the Spanish company Pleiades Astrophoto. It is a modular application for chroma noise reduction based on two principal algorithms: the SGBNR (Selective Gaussian Blur Noise Reduction) and the SCNR (Subtractive Chromatic Noise Reduction). The first one is an efficient method to reduce the noise in the medium and large-dimensional scales, while the second one is a technique developed to remove noise in the green channel of coloured deep-sky astrophotos.
The SGBNR is designed to smooth image areas where there are few or no details, but preserving small structures and contrast. In order to achieve this goal it uses a lowpass filter with a strength that depends on edge features of the image. The filtering intensity is driven by the filter size, the "Amount" parameter, which fixes the percentage of the original pixel value to be preserved, and the "Edges Protection Threshold", which evaluates the "edgeness" degree of each pixel (also depending on the luminance level) and modulates the filter strength consequently.
If  is the SGBNR-processed pixel value corresponding to an original pixel value
is the SGBNR-processed pixel value corresponding to an original pixel value  and
and  is the "Amount" parameter, then the resulting pixel value
is the "Amount" parameter, then the resulting pixel value  is given by
is given by

where pixel values are in the normalized  interval.
interval.
During low-pass filtering, each pixel is assigned to a neighborhood of surrounding pixels. Edge protection works by first estimating a significant brightness level for the neighborhood. Then it compares the central pixel with each neighbor and computes a weighted difference. When a neighbor pixel, whose difference with the central pixel exceeds the corresponding edges protection threshold (either for bright or dark sides, depending on the sign of the difference), is found, then a corrective function is applied to the neighbor pixel in order to give it more opportunities to survive after the low-pass filtering. This allows to preserve small-scale image features and contrast. Note that too high value of the threshold can allow excessive low-pass filtering, whilst too low value of the threshold can generate artifacts. The SGBNR can also be applied recursively. In this case the threshold parameters are less critical and the edge protection mechanism is more efficient.
The SCNR process has been designed mainly to remove green noisy pixels. With the exception of some planetary nebulae, there is no green object in the deep-sky: there are no green stars and emission nebulae are deeply red, whilst reflection nebulae are blue; so if there are green pixels on a color balanced, deep-sky astrophoto, they will be noise; consequently such kind of noise can be removed easily and very efficiently. The SCNR process is defined by two parameters: the "Protection Method" and "Amount". In order to avoid destroying correct green data, four protection methods have been implemented. They perform a weighted average on the new green value depending on the red and blue values. The parameter "Amount" controls the contribution of the original green value.
The main drawback of the SCNR is that it can introduce a magenta cast to the sky background, which must be controlled by a careful dosage of the Amount parameter. PixInsight contains also the "ATrousWaveletTransform", a rich tool able to reduce the high-frequencies chroma noise using the wavelet decomposition. It exploits median and erosion/dilation morphological filters for specific noise reduction tasks, such as impulsive noise removal.
The panorama of consumer solutions available as plug-in or as standalone application includes also Noise Ninja [18] and Dfine [19]. Noise Ninja is a powerful software produced by the PictureCode LLC that removes chroma noise with an algorithm in the wavelet domain. It is a good trade-off between noise reduction and details preservation. The main feature is the ability to limit the introduction of edge blurring and color bleeding, which are defects not properly managed by conventional wavelets.
Dfine is made for both amateurs and experts. The automatic process consists of two steps: to measure the noise and to remove the noise. The application allows the full control of the noise reduction process, too. The entity of the noise can be measured manually depending on the features of the image under processing, by selecting a region of the image affected by noise and then by filtering only a specific color range or a specific object. The default noise reduction method is named "Control Points" and it allows the user to select different parts of the image and to tune the filter strength. The statistics collected on the selected data are used to perform the noise reduction on the whole image. The Control Points method allows the user also to manage separately the chroma and contrast noise. Moreover, the so-built noise profile can be saved and applied for further executions. The "Color Range" method is designed to preserve specific colors. It is also possible to apply the algorithm only to specific objects, for example, on the skin, or processing the background of the image only.
All the algorithms discussed above require interaction with the user. This paper presents the DCT-CNR (Discrete Cosine Transform-Chroma Noise Reduction), an efficient chroma noise reduction algorithm based on soft-thresholding on DCT data and designed to be integrated in the Image Generation Pipeline (IGP) [20], which allows any image system to yield the final color image starting from sensor data. Each step of the chain affects the noise level in the image; so reducing the noise during the generation process is a crucial step to improve the output quality. The DCT-CNR allows to limit chroma noise locally without using interaction and it can be easily embedded in JPEG encoders, which usually is the final step of the IGP, with negligible computational overload.
The rest of the paper is organized as follows: Section 2 briefly describes the problem of the noise reduction in the DCT domain; Section 3 presents the DCT-CNR in details; Section 4 discusses experimental results and comparative tests; the last section contains conclusion and final remarks.
2. Noise Reduction and DCT
The (white) noise affects all the DCT coefficients and it implies not only a degradation of the image but also a reduction of the efficiency of the encoding process performed both in still image and in video sequences. The number of DCT zero-coefficients decreases due to noise; so the run-length coding used in JPEG [21] and MPEG [22] standards suffers a loss in terms of compression rate.
A widely used technique for noise reduction consists of adjusting each frequency component of the noisy signal accordingly with a function properly defined, usually called coring function [11]. The basic idea is that low-energy DCT coefficients bring small information and are highly influenced by noise. On the other hand, high-energy DCT coefficients carry high information and are slightly influenced by noise. Thus, the coefficients with large amplitudes can be considered reliable and they should be preserved; on the contrary, coefficients with small amplitude are considered not reliable and their contribution should be reduced or discarded.
The following coring function (Figure 1), known as soft-threshold, formalizes the concept:

where  is one of the DCT coefficients of the noisy signal;
is one of the DCT coefficients of the noisy signal;  is the noise-reduced DCT coefficient;
is the noise-reduced DCT coefficient;  is the coring threshold.
is the coring threshold.
3. Chroma Noise Reduction in DCT Domain
The proposed algorithm, named DCT-CNR (Discrete Cosine Transform-Chroma Noise Reduction), consists of performing a soft-threshold to the chrominance components of the image preserving the luminance and the DC coefficients of each DCT 8 × 8 chrominance block of the image to be coded.
Any image device contains an IGP [20], which transforms the sensor data in the final RGB image. Each step of the pipeline affects the output noise level, which depends on many factors, including sensor type, pixel dimensions, temperature, exposure time, and ISO speed. An effective noise reduction strategy should be distributed (limiting the noise introduction or amplification in each block of the chain). The DCT-CNR has been developed to be easily integrated into the JPEG encoder, which is placed at the end of the pipeline to perform the compression, providing chroma noise reduction without resources overload.
The crucial step of the algorithm is the coring threshold definition. It should be big enough to reduce the noise and small enough to preserve the details. Moreover, it should be different for each block to take into account the information content, avoiding texture or detailed regions destruction and performing a strong noise reduction in the flat areas, where the chroma noise is more visible. A fixed threshold definition may not be a good solution because it could not manage differently the details in regions with different features.
An appropriate threshold definition has to exploit local measures able to provide a reliable color noise characterization. Moreover, each 8 × 8 block of DCT coefficients must be classified. To achieve such results the threshold has been defined using the following measures.
-
(i)
Robustness" to noise: a statistical analysis of a large set of images affected by color noise showed that some AC coefficients are more sensitive to noise than others. A constant weight has been assigned to each AC coefficient in dependence on its position in the block, in order to preserve the most robust coefficients (which carry suitable information) and discard the ones that, with high probability, are corrupted by noise.
-
(ii)
Edgeness" of the block: if a block contains an edge or a detail, its information content should be maintained untouched, whilst a homogeneous block should be strongly corrected. In this paper an edgeness measure has been used. It is basically a fuzzy measure describing the probability that a block contains an edge.
An adaptive threshold, varying for each DCT block, is defined combining robustness and edgeness, as described in the following subsections.
3.1. Block Classification: Coefficients Robustness to Noise
Battiato et al. [23, 24] proposed a method that combines a theoretical/statistical approach with the Human Visual System response function to optimizes the JPEG quantization tables for specific classes of images and specific viewing conditions [25]. The optimal parameters for tables' modification are learned, after an extensive training phase, for three classes: document, landscape, and portrait. Such methodology has been employed to process two set of images of the same scene. First, the images have been acquired at low-light conditions, in order to collect a sufficient noise statistics; then the ideal luminance conditions have been used to acquire the corresponding "clean" images. Analyzing the quantization coefficients modified by the algorithm, the robustness of each DCT AC value has been estimated. The table of the coefficients weights is shown in Figure 2. As visible, the higher the weight is, the more robust is the coefficient (the DC value is not modified) and the higher is its probability to remain unchanged.
3.2. Block Classification: Edgeness
Generally speaking, we can assume that, in the chroma components of an image, two adjacent DCT blocks belong to a monochromatic region if they have a similar DC value and only few AC coefficients are not zero. Instead, blocks with different DC values and many nonzero AC coefficients correspond to zones with color transitions. Since the noise affects all the DCT values, the basic problem is to extract each block's features to correctly classify it. A single value varying in the range  and describing the degree of edgeness of a block is computed in four steps:
and describing the degree of edgeness of a block is computed in four steps:
-
(1)
energy estimation along directions,
-
(2)
energy cross-analysis,
-
(3)
fuzzy estimation of the block activity,
-
(4)
edgeness computation.
Coudoux et al. in [26] use a block classification based on AC energies of DCT coefficients. In particular, the DCT block coefficients are divided into four classes: low activity, vertical, horizontal, and diagonal. Such strategy has been implemented to perform the first step. The directional indexes  ,
,  , and
, and  described in Figure 3 are computed.
described in Figure 3 are computed.
The "energy cross-analysis" is needed to check if a preferred direction exists in the block under examination. The following values are computed:

Three fuzzy sets are then defined to describe the edgeness of the block:

where  .
.
 ,
,  , and
, and  represent the degree of membership to the fuzzy sets describing the horizontal, diagonal and vertical edgeness, respectively (Figure 4).
represent the degree of membership to the fuzzy sets describing the horizontal, diagonal and vertical edgeness, respectively (Figure 4).
Given the "direction vectors":

the final step consists of computing the edgeness as follows:

where

 and
and  estimate the distance among the edgeness measures, which are indicator of the presence of a master direction in the block under examination.
estimate the distance among the edgeness measures, which are indicator of the presence of a master direction in the block under examination.
The edgeness value is used to drive the noise reduction intensity, which depends on the threshold computation defined in the following subsection. Several cases could happen.
-
(a)
Very HIGH values of edgeness: both
 and
and  have values close to 1. This means that a dominant direction exists and the block contains an edge, and so it has to be preserved (Figure 5(a)).
have values close to 1. This means that a dominant direction exists and the block contains an edge, and so it has to be preserved (Figure 5(a)). -
(b)
Very LOW values of edgeness (close to zero): one has the following.
-
(i)
Both
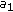 and
and 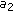 are low, but the values in DIR are high. In this case all the directions are strong, so the block has probably fine textures or noise fluctuations, and a strong filtering is required. In other words, most of its coefficients have to be reduced or discarded.
are low, but the values in DIR are high. In this case all the directions are strong, so the block has probably fine textures or noise fluctuations, and a strong filtering is required. In other words, most of its coefficients have to be reduced or discarded. -
(ii)
 and
and 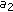 are low and the DIR values are low. The block has very low activity (Figures 5(b) and 5(c)), so it belongs probably to a homogeneous region, and a strong filtering can be performed.
are low and the DIR values are low. The block has very low activity (Figures 5(b) and 5(c)), so it belongs probably to a homogeneous region, and a strong filtering can be performed.
-
(i)
-
(c)
Average value of edgeness: two directions are greater than the third one, and so a sort of media filtering is needed.
3.3. Threshold Definition
For each 8 × 8 DCT block, the threshold is given by

where
-
(i)
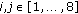 are the indexes of the table containing the robustness weights (Figure 2);
are the indexes of the table containing the robustness weights (Figure 2); -
(ii)
maxDir is the maximum of the vertical, horizontal and diagonal AC coefficients (Figure 6);
-
(iii)
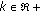 drives the filtering strength. Usually it varies in the range
drives the filtering strength. Usually it varies in the range 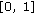 .
.
The threshold computation is the key step of the algorithm. The higher the threshold is, the bigger is the number of DCT coefficients whose contribution is reduced or discarded. The real parameter  allows to increase or to reduce the threshold which drives the filter strength.
allows to increase or to reduce the threshold which drives the filter strength.
3.4. Complexity
The computational cost of the algorithm has been estimated considering the operations per pixel needed to process 4 : 2 : 0 subsampled images. The DCT complexity is not included in the count, and so the major cost of the algorithm is limited to the threshold computation defined in (1). Table 1 summarizes the results in terms of operations per pixel. The computational cost is obtained dividing the number of operations required by the size of the 4 : 2 : 0 subsampled DCT block. Note that the complexity is very low: less than one expensive operation per pixel (division and multiplication) has to be performed.
4. Experiments
Several tests have been done to evaluate the performances of the DCT-CNR. The results are described in the following subsections. The objective metric Peak Signal-to-Noise Ratio (PSNR) has been used to estimate the effectiveness of the algorithm as discussed in Section 4.1. Section 4.2 explains the algorithm effects on the JPEG compression. Section 4.3 presents comparative tests with other color noise reduction techniques.
4.1. DCT-CNR Performances Evaluation Using PSNR
In order to proof the effectiveness of the DCT-CNR, chroma noise has been added to a set of ten "clean" images and the Peak Signal-to-Noise Ratio (PSNR) has been computed before and after the application of the algorithm. The cleaned input images (shown in Figure 7) are used as references for PSNR computation. Since chroma noise affects predominantly the low frequencies, it has been generated with Photoshop Gaussian noise tool and performing a low-pass filtering in order to spread the blobs. A set of images affected by "synthetic" chroma noise has been obtained by varying the amount of input Gaussian noise. Then the DCT-CNR has been applied and the PSNR of the input and the output images have been compared. Table 2 summarizes the results obtained as the noise amount grows. The most appreciable results are achieved with added noise with  . In such case the improvement on average is of 0.61 dB. For lower noise amount (
. In such case the improvement on average is of 0.61 dB. For lower noise amount ( ) the PSNR increase is lower (about 0.2 dB on the average). "Lena" and "Baboon" images suffer of a reduction of the measured quality in the cases of noise with
) the PSNR increase is lower (about 0.2 dB on the average). "Lena" and "Baboon" images suffer of a reduction of the measured quality in the cases of noise with  and
and  , due to the slight blocking effect introduced by the DCT coefficients manipulation. The PSNR in all the other images is increased.
, due to the slight blocking effect introduced by the DCT coefficients manipulation. The PSNR in all the other images is increased.
Figure 8 shows the results obtained on the "Fruits" image. The quality improvement of the output is slight in the case of added noise with  (just 0.05 PSNR dB), but it grows with the additional noise (the gain achieves the 0.52 dB of PSNR in the case of added noise with
(just 0.05 PSNR dB), but it grows with the additional noise (the gain achieves the 0.52 dB of PSNR in the case of added noise with  ). However the color noise reduction is visually perceivable in any case.
). However the color noise reduction is visually perceivable in any case.
4.2. DCT-CNR: Pro and Cons
In order to evaluate the effect of the DCT-CNR on the compression step, it has been integrated into the open source cjpeg encoder [27]. The reference image has been generated coding the input with the DCT-CNR disabled. Figure 9 shows an image of the Macbeth chart acquired in low-light conditions. The 200% enlarged details show the pro and cons of the algorithm: in the upper left highlighted square, the homogeneous regions have been cleaned preserving the strong edges. In the lower left detail, a blocking effect is visible. In such critical case the 8 × 8 DCT block analysis provided a different classification among adjacent blocks due to the adaptive threshold computation. Note that the image has been encoded at the maximum quality factor; so there are no quantization errors added by the JPEG encoder. However, the blocking effect, which is also a well-known drawback of the JPEG algorithm, is progressively masked increasing the compression rate. Figure 10 shows one more example. At lower compression quality (denoted by  in the figure), the blocking effect introduced by the compression makes the artifacts less perceivable due to the chroma noise reduction algorithm.
in the figure), the blocking effect introduced by the compression makes the artifacts less perceivable due to the chroma noise reduction algorithm.
This example shows a critical case. The images are 200% zoomed. On the left there are the images obtained by applying the JPEG encoder and by disabling the chroma denoiser; on the right are show the outputs of the JPEG with the chroma noise reduction enabled. As visible, some blocking artefacts are introduced, but they are progressively masked at lower bit rate.
Figure 11 proofs the efficiency of the DCT-CNR on homogeneous regions. The highlighted detail shows the appreciable reduction of the color noise in the image.
4.3. DCT-CNR: Comparative Testing
The DCT-CNR have been compared with two other techniques. The first one is based on blurring the  and
and  channels in CIELAB domain through a median or Gaussian blurring [4]. The results obtained by applying the Gaussian filter to the chroma channels after color transform from RGB to CIELAB domain has been analyzed in terms of PSNR and visual quality of the output images used in the experiments described in Section 4.1. In the following discussion this method is referred as Chroma Blurring (CB). The second technique is the Nokia's Dfine Photoshop Plugin [19]. As discussed in Section 1 such approach is semiautomatic: it estimates the chroma noise amount by computing statistics on homogeneous areas of the image in different luminance values. Additional regions could be selected by the user that manages the noise reduction process through a set of parameters. Table 1 shows the PSNR results of the three algorithms. The performances vary with the amount of input noise. In the case of added noise with
channels in CIELAB domain through a median or Gaussian blurring [4]. The results obtained by applying the Gaussian filter to the chroma channels after color transform from RGB to CIELAB domain has been analyzed in terms of PSNR and visual quality of the output images used in the experiments described in Section 4.1. In the following discussion this method is referred as Chroma Blurring (CB). The second technique is the Nokia's Dfine Photoshop Plugin [19]. As discussed in Section 1 such approach is semiautomatic: it estimates the chroma noise amount by computing statistics on homogeneous areas of the image in different luminance values. Additional regions could be selected by the user that manages the noise reduction process through a set of parameters. Table 1 shows the PSNR results of the three algorithms. The performances vary with the amount of input noise. In the case of added noise with  , the DCT-CNR has the best results on the average, but the PSNR variations with the CB and Dfine are small. The Dfine performances slowly decline with the noise increase from
, the DCT-CNR has the best results on the average, but the PSNR variations with the CB and Dfine are small. The Dfine performances slowly decline with the noise increase from  to
to  and the average loss is of about 1.5 dB, whilst the CB degradation is about 2.2 dB and the DCT-CNR loss is about 2.4 dB. Such data show that the Dfine performances improve at high noise levels. But the PSNR is not always linked to the visual quality of the output. A strong filtering able to destroy the noise also provides details loss with related quality degradation. It is the case of the Dfine and the CB(Table 3).
and the average loss is of about 1.5 dB, whilst the CB degradation is about 2.2 dB and the DCT-CNR loss is about 2.4 dB. Such data show that the Dfine performances improve at high noise levels. But the PSNR is not always linked to the visual quality of the output. A strong filtering able to destroy the noise also provides details loss with related quality degradation. It is the case of the Dfine and the CB(Table 3).
The problem is evident in the image with large textured regions, as "Baboon" (Figure 12). In this example the different PSNR values correspond to the different image qualities. Even if the Dfine allows to reduce an appreciable amount of noise, the strong filtering yields a contrast decrease in the output. CB and DCT-CNR allow preserving the details at the cost of a less evident noise reduction. Figure 13 summarizes the results obtained processing the "Parrot" image. The Dfine achieves the best results in terms of PSNR, but the visual analysis reveals the lost of noticeable details and the output appears too flat. Figure 14 shows an objective result. The 200% enlarged detail of the Ship image shows that the Dfine is too aggressive and it destroys the textured region at all, whilst the CB and the DCT-CNR outputs achieve a higher quality, even if their PSNR is lower.
But a fair comparison among the algorithms must take into account their complexity and the specific application they have been developed to. The DCT-CNR is fully automatic and it has been developed to be implemented as additional feature of a JPEG encoder with negligible additional hardware and computational resources. The main constraint driving the algorithm design was to reduce the computational and memory costs. Most of the chroma noise reduction algorithms, Dfine and CB included, have been developed for postprocessing. Their application into an IGP implies adding to the chain a block dedicated to chroma noise reduction, with consequently increase of resources requirement.
5. Conclusion
A simple and efficient algorithm for chroma noise reduction, called DCT-CNR, has been presented. It operates in the DCT data domain, managing the chromatic components only. The DCT-CNR has a very low complexity in terms of computational costs and it also requires few hardware resources because it could be easily integrated in the JPEG compression block of an IGP of a digital still camera improving the final image quality without additional complexity. It is based on a DCT block classification and it is able to preserve the zones of the image containing details or edges by applying a stronger filtering on the flat regions.
References
Adams JE Jr., Hamilton JF Jr., Smith CM: Reducing Color Aliasing Artifacts from Color Digital Images. US Patent No. US 6 927 804 B2, August 2005
Kessler D, Nutt ACG, Palum RJ: Anti-Aliasing Low-Pass Blur Filter for Reducing Artifacts in Imaging. Patent No. US 5 684 293 B1, November 1997
McGettigan AD, Ockenfuss G: Anti-Aliasing Optical Filter for Image Sensors. US Patent No. 7 088 510 B2, August 2006
Hamilton JF Jr., Adams JE Jr.: Smoothing a Digital Color Image Using Luminance Values. U.S. Patent No. 6 697 107, Febraury 2004
Gonzales RC, Woods RE: Digital Image Processing. Addison Wesley, Reading, Mass, USA; 1993.
Adams JE Jr., Hamilton JF Jr.: Removing Chroma Noise from Digital Images by Using Variable Shape Pixel Neighborhood Regions. European Patent No. EP 1 093 087 B1, September 2000
Uniform Color Spaces—Color Difference Equations, Psychometric Color Terms. Commission Internationale de L'Eclairage, Paris, France; 1978.
Wu Q, Schulze MA, Castleman KR: Steerable pyramid filters for selective image enhancement applications. Proceedings of the IEEE International Symposium on Circuits and Systems (ISCAS '98), June 1998 5: V-325-V-328.
Donoho DL: Denoising by soft-thresholding. IEEE Transactions on Information Theory 1995,41(3):613-627. 10.1109/18.382009
Balster EJ, Zheng YF, Ewing RL: Feature-based wavelet shrinkage algorithm for image denoising. IEEE Transactions on Image Processing 2005,14(12):2024-2039.
Van Roosmalen PMB, Lagendijk RL, Biemond J: Embedded coring in MPEG video compression. IEEE Transactions on Circuits and Systems for Video Technology 2002,12(3):205-211. 10.1109/76.993441
Donoho DL, Johnstone JM: Ideal spatial adaptation by wavelet shrinkage. Biometrika 1994,81(3):425-455. 10.1093/biomet/81.3.425
Donoho DL, Johnstone IM, Kerkyacharian G, Picard D: Wavelet shrinkage: asymptopia? Journal of the Royal Statistical Society Series B 1995,57(2):301-369.
Chang SG, Yu B, Vetterli M: Adaptive wavelet thresholding for image denoising and compression. IEEE Transactions on Image Processing 2000,9(9):1532-1546. 10.1109/83.862633
Tomasi C, Manduchi R: Bilateral filtering for gray and color images. Proceedings of the IEEE 6th International Conference on Computer Vision, January 1998 839-846.
Zhang M, Gunturk BK: Multiresolution bilateral filtering for image denoising. IEEE Transactions on Image Processing 2008,17(12):2324-2333.
PixInsight Image Processing Software http://www.pixinsight.com/
Noise Ninja http://www.picturecode.com
Battiato S, Messina G, Castorina A: Exposure correction for imaging devices: an overview. In Single-Sensor Imaging, Methods and Applications for Digital Cameras, Image Processing Series. Edited by: Lukac R. CRC Press, Boca Raton, Fla, USA; 2008.
Wallace GK: The JPEG still picture compression standard. Communications of the ACM 1991,34(4):30-44. 10.1145/103085.103089
ISO/IEC JTC1/SC29/WG11 N 2502 Final Draft of International Standard MPEG-4
Battiato S, Mancuso M: Psychovisual and Statistical Optimization of Quantization Tables for DCT Compression Engines. European Patent No. EP 20010830738, 2003
Battiato S, Mancuso M, Bosco A, Guarnera M: Psychovisual and statistical optimization of quantization tables for DCT compression engines. Proceedings of IEEE International Conference on Image Analysis and Processing (ICIAP '01), September 2001, Palermo, Italy 602-606.
Bosco A, Battiato S, Bruna A, Rizzo R: Noise reduction for CFA image Sensors exploiting HVS behaviour. Sensors 2009,9(3):1692-1713. 10.3390/s90301692
Coudoux F-X, Gazalet M, Corlay P: A DCT-domain postprocessor for color bleeding removal. Proceedings of the European Conference on Circuit Theory and Design, August-September 2005 1: 209-212.
Independent JPEG Group http://www.ijg.org/
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Buemi, A., Bruna, A., Mancuso, M. et al. Chroma Noise Reduction in DCT Domain Using Soft-Thresholding. J Image Video Proc 2010, 323180 (2011). https://doi.org/10.1155/2010/323180
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1155/2010/323180




 and
and  have values close to 1. This means that a dominant direction exists and the block contains an edge, and so it has to be preserved (Figure
have values close to 1. This means that a dominant direction exists and the block contains an edge, and so it has to be preserved (Figure 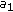 and
and 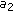 are low, but the values in DIR are high. In this case all the directions are strong, so the block has probably fine textures or noise fluctuations, and a strong filtering is required. In other words, most of its coefficients have to be reduced or discarded.
are low, but the values in DIR are high. In this case all the directions are strong, so the block has probably fine textures or noise fluctuations, and a strong filtering is required. In other words, most of its coefficients have to be reduced or discarded. and
and 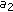 are low and the DIR values are low. The block has very low activity (Figures
are low and the DIR values are low. The block has very low activity (Figures 
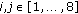 are the indexes of the table containing the robustness weights (Figure
are the indexes of the table containing the robustness weights (Figure 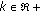 drives the filtering strength. Usually it varies in the range
drives the filtering strength. Usually it varies in the range 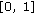 .
.








 . Even if the highest PSNR is achieved using the Dfine (left), the quality of the output of CB (center) and DCT-CNR (right) is better because the texture in the rocks is better preserved.
. Even if the highest PSNR is achieved using the Dfine (left), the quality of the output of CB (center) and DCT-CNR (right) is better because the texture in the rocks is better preserved.