- Research Article
- Open access
- Published:
Rigid Registration of Renal Perfusion Images Using a Neurobiology-Based Visual Saliency Model
EURASIP Journal on Image and Video Processing volume 2010, Article number: 195640 (2010)
Abstract
General mutual information- (MI-) based registration methods treat all voxels equally. But each voxel has a different utility depending upon the task. Because of its robustness to noise, low computation time, and agreement with human fixations, the Itti-Koch visual saliency model is used to determine voxel utility of renal perfusion data. The model is able to match identical regions in spite of intensity change due to its close adherence to the center-surround property of the visual cortex. Saliency value is used as a pixel's utility measure in an MI framework for rigid registration of renal perfusion data exhibiting rapid intensity change and noise. We simulated varying degrees of rotation and translation motion under different noise levels, and a novel optimization technique was used for fast and accurate recovery of registration parameters. We also registered real patient data having rotation and translation motion. Our results show that saliency information improves registration accuracy for perfusion images and the Itti-Koch model is a better indicator of visual saliency than scale-space maps.
1. Introduction
Image registration is the process of aligning two or more images which may be taken at different time instances, from different views or by different sensors (or modalities in medical imaging applications). The floating image(s) is (are) then registered to a reference image by estimating a transformation between them. Image registration plays a vital role in many applications such as video compression [1], video enhancement [2], scene representation [3], and medical image processing [4].
Medical image registration has acquired immense significance in automated or semiautomated medical image analysis, intervention planning, guidance, and assessment of disease progression or effects of treatment. Some of the applications have been in the areas of brain imaging [5], kidney (renal) perfusion images [6], and radiological images [7]. Over the years, rigid registration algorithms have used mutual information (MI) [8, 9], Fourier transforms [10–12], correlation-based methods [13–15] and attribute vectors [16]. For registering dynamic kidney perfusion images three approaches were tested in [17], namely, template matching, Fourier transforms, and cross correlation, and the Fourier transform-based approach was found to give the best performance. A method for correcting image misregistration due to organ motion in dynamic magnetic resonance (MR) images combines mutual correspondence between images with transform invariant features [18]. Other methods for registration of renal perfusion MR images are based on a combination of wavelet and Fourier transforms [6] and a contrast invariant similarity measure [19].
In dynamic contrast enhanced (DCE) MRI, a contrast agent (e.g., Gd-DTPA) is injected into the blood stream. The resulting images exhibit rapid intensity change in an organ of interest. Apart from intensity change, images from a single patient are characterized by noise and movement of the organ due to breathing or patient motion. Registering images with such rapid intensity changes is a challenge for conventional registration algorithms. Although previous works [6, 17–19] demonstrate good results in registering renal perfusion MR images, they fail to incorporate the contribution of the human visual system (HVS) in such tasks. The HVS is adept at distinguishing objects in noisy images, a challenge yet to be completely overcome by object recognition algorithms. Humans are also highly capable of matching objects and regions between a pair of images in spite of noise or intensity changes. We believe it is worthwhile to investigate whether a model of the HVS can be used to register images in the presence of intensity change. In this paper, we use a neurobiology-based HVS model for rigid registration of kidney MRI in an MI framework. As we shall, see later MI is a suitable framework to include the contribution of the HVS.
Most MI-based registration methods treat all voxels equally. But a voxel's utility or importance would vary depending upon the registration task at hand. For example, in renal perfusion MRI a voxel in the renal cortex has greater significance in registration than a voxel in the background even though they may have the same intensity. Luan et al. in [20] have defined a voxel's importance based on its saliency and used it in a quantitative-qualitative mutual information (QMI) measure for rigid registration of brain MR images. Saliency refers to the importance ascribed to a voxel by the HVS. Different computational models have been proposed to determine saliency maps of images [21, 22]. An important characteristic of the HVS is its ability to match the same landmark in images exhibiting intensity change (as in DCE images). An accurate model of the HVS should be able to imitate this property and assign similar importance (or utility) values to corresponding landmarks in a pair of images. The entropy-based saliency model used in [20], called scale-space maps, fails to achieve the desired objectives for DCE images.
Scale-space maps [21] calculate the entropy over different scales around a pixel's neighborhood and the maximum entropy at a particular scale is used to calculate the saliency value. When there is a change in intensity due to contrast enhancement the entropy (and hence saliency) value of a pixel also changes. As a result, the same landmark in two different images has different utility measures. But it is desirable that a landmark have the same utility value in different images. In contrast, the neurobiology based saliency model of [22] assigns the same importance to corresponding landmarks and has been shown to have a high correlation with human fixations [23]. Besides, it has advantages over scale-space maps in terms of robustness to noise and computational complexity. Therefore, we hypothesize that a neurobiological model of saliency would produce more accurate results than scale-space maps for rigid registration of kidney perfusion images. Saliency models have also been used for computer vision tasks like image retrieval [24] and image interpolation [25].
In this paper, we investigate the usefulness of a neurobiology-based saliency model for registering renal perfusion images. Our paper makes the following contributions. First, it investigates the effectiveness of a computational model of the HVS for image registration within the QMI framework proposed in [20]. Previously used saliency models are limited by their inaccurate correspondence with actual human fixations and sensitivity to noise. Our work is different from [20] in the use of saliency models. Second, we perform a detailed analysis of the effectiveness of different mutual information-based similarity measures, with and without using saliency information, for the purpose of registering renal perfusion images. This gives an idea of the effectiveness of different saliency methods. Third, we use a randomized optimization scheme which evaluates greater number of candidate solutions, which minimizes the possibility of being trapped in a local minimum and increases registration accuracy. The rest of the paper is organized as follows. In Section 2, we describe the neurobiology-based saliency model, theoretical foundations of MI-based registration and our optimization scheme. Sections 3 and 4, respectively, give details about our method and experimental results. Finally we conclude with Section 5.
2. Theory
2.1. Saliency Model
Visually salient regions in a scene are those that are more "attractive" than their neighbors and hence draw attention. Saliency in images has been defined on the basis of edges [26] and corners [27]. Studies have also shown that salient regions are those that have maximum information content [28]. In this regard, entropy has been used to define scale-space maps for saliency [21]. The entropy-based saliency map, however, has the following limitations in determining saliency.
-
(1)
The changing intensity of perfusion images assigns different entropy and hence saliency values to corresponding pixels in an image pair exhibiting intensity change. This is undesirable when matching contrast enhanced images.
-
(2)
There is the inherent problem of choosing an appropriate scale. For every voxel, the neighborhood (scale) that maximizes the local entropy is chosen to be its optimal scale resulting in unnecessary computational cost.
-
(3)
Presence of noise greatly affects the scale-space map which results in erroneous saliency values. Since local entropy gives a measure of the information content in a region, presence of noise can alter its saliency value.
-
(4)
The scale-space saliency map does not truly determine what is salient to the human eye. An entropy-based approach takes into account distribution of intensity in a local neighborhood only. Thus the information derived is restricted to a small area in the vicinity of the pixel.
Considering the above drawbacks, the neurobiology based model performs better for the following reasons.
-
(1)
An important aspect of the model is its center-surround principle which determines how different a pixel is from its surroundings. As long as a pixel has feature values different from its surroundings its saliency value is preserved, thus acting as a robust feature. This is better than the entropy model where the intensity distribution leads to different saliency values when intensity changes due to contrast enhancement.
-
(2)
By representing the image in the form of a Gaussian pyramid, the need for determining the appropriate scale for every voxel does not arise.
-
(3)
Inherent to the model is the process of lateral inhibition that greatly contributes to suppressing noise in the saliency map.
-
(4)
The model, when used to identify salient regions in a scene, has high correlation with actual human fixations.
The model calculates a saliency map by considering intensity and edge orientation information from a given image. Saliency at a given location is determined primarily by the contrast between this location and its surroundings with respect to the image features. The image formed on the fovea of the eye is the central object on which a person is focusing his attention resulting in a clear and sharp image. Regions surrounding the central object have a less clearer representation on the retina. To simulate this biological mechanism, an image is represented as a Gaussian pyramid comprising of layers of subsampled and low-pass filtered images. The central representation of the image on the fovea is equivalent to the image at higher spatial scales, and the surrounding regions are obtained from the lower spatial scales. The contrast is thus the difference between the various feature maps at these scales.
Let  and
and  denote a feature map (intensity, edge orientation, etc.) at scale c and
denote a feature map (intensity, edge orientation, etc.) at scale c and  , respectively. The contrast map
, respectively. The contrast map  is defined as
is defined as

where  denotes center-surround difference, the center is given by level
denotes center-surround difference, the center is given by level  and the surround is given by level
and the surround is given by level  ,
,  in the Gaussian pyramid. Thus, we have
in the Gaussian pyramid. Thus, we have  contrast maps for every feature. Although the original model uses three features, including color, intensity, and edge information, we use only intensity and edge information because our datasets were in grayscale. The edge information is obtained from the image by using oriented Gabor filters [29] at different orientation angles (
contrast maps for every feature. Although the original model uses three features, including color, intensity, and edge information, we use only intensity and edge information because our datasets were in grayscale. The edge information is obtained from the image by using oriented Gabor filters [29] at different orientation angles ( ,
,  ,
,  , and
, and  ). In total
). In total  feature maps are obtained,
feature maps are obtained,  for edge orientation and
for edge orientation and  for intensity.
for intensity.
The feature maps represent different modalities and varying extraction mechanisms. In combining them, salient objects appearing strongly in a few maps may be masked by noise or less salient objects present in a larger number of maps. Therefore, it is important to normalize them before combination. A map normalization operator  is used which globally promotes maps where a small number of strongly conspicuous locations are present while suppressing maps containing numerous locations of similar conspicuity.
is used which globally promotes maps where a small number of strongly conspicuous locations are present while suppressing maps containing numerous locations of similar conspicuity.  consists of the following steps.
consists of the following steps.
-
(1)
Normalize the values in the map to a fixed range
 to eliminate modality or feature-dependent amplitude differences. We set
to eliminate modality or feature-dependent amplitude differences. We set  in our experiments.
in our experiments. -
(2)
Find location of the map's global maxima,
 , and calculate the average
, and calculate the average 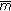 of its other local maxima.
of its other local maxima. -
(3)
Globally multiply the map by
 .
.
The biological motivation behind  is that it coarsely replicates lateral inhibition mechanisms in which neighboring similar features inhibit each other via specific, anatomically defined connections [30]. The feature maps are combined into two conspicuity maps,
is that it coarsely replicates lateral inhibition mechanisms in which neighboring similar features inhibit each other via specific, anatomically defined connections [30]. The feature maps are combined into two conspicuity maps,  for intensity and
for intensity and  for edge orientation. The conspicuity maps are again normalized and the final saliency map
for edge orientation. The conspicuity maps are again normalized and the final saliency map  is obtained as the average of the normalized conspicuity maps(2)
is obtained as the average of the normalized conspicuity maps(2)

2.1.1. Saliency Map in  D
D
The gap between slices of the original volume is  mm which does not provide sufficient information along the
mm which does not provide sufficient information along the  -axis to extend each step of the saliency map to
-axis to extend each step of the saliency map to  D. Intensity maps can be obtained directly from the data but calculating orientation maps proves to be challenging as
D. Intensity maps can be obtained directly from the data but calculating orientation maps proves to be challenging as  D oriented Gaussian filters are computationally intensive. Therefore, for each slice of the
D oriented Gaussian filters are computationally intensive. Therefore, for each slice of the  D volume, we calculate its
D volume, we calculate its  D saliency map which is subsequently used for registration.
D saliency map which is subsequently used for registration.
2.2. Rigid Registration
Rigid registration requires us to align a floating image (volume) with respect to a reference image (volume) by correcting any relative motion between them. For simplicity, we describe the registration framework in terms of  D images but our experiments were for
D images but our experiments were for  D volumes. Let
D volumes. Let  be the floating image (volume for
be the floating image (volume for  D data) which is to be registered to a reference image
D data) which is to be registered to a reference image  . For
. For  D volumes there are 6 degrees of freedom (i.e., translation and rotation along each of
D volumes there are 6 degrees of freedom (i.e., translation and rotation along each of  -,
-,  - and
- and  -axis) while
-axis) while  D images have
D images have  degrees of freedom. The similarity between two images is determined from the value of a similarity measure which depends upon the type of images being registered. The parameters for translation and rotation that give maximum value of the similarity measure are used to register the floating image.
degrees of freedom. The similarity between two images is determined from the value of a similarity measure which depends upon the type of images being registered. The parameters for translation and rotation that give maximum value of the similarity measure are used to register the floating image.
To determine the effectiveness of the neurobiology model of saliency, we used it in a QMI-based cost function for rigid registration. This cost function combines saliency information (or utility measure) with the MI of the two images to evaluate the degree of similarity between them. A joint saliency (or joint utility) histogram, similar to a joint intensity histogram, is used to determine the cooccurrence of saliency values in the saliency maps of the images under consideration. We follow the QMI definition and formulation of [20].
2.2.1. Quantitative-Qualitative Measure of Mutual Information
In [31], a quantitative-qualitative measure of information in cybernetic systems was proposed which puts forth two aspects of an event: a qualitative part related to the fulfillment of the goal in addition to the quantitative part which is related to the probability of occurrence of the event. The self-information of an event  with probability of occurrence
with probability of occurrence  is given by
is given by  [32]. In image processing, an event is the intensity of a pixel and an entire image is a set of events. Thus, according to Shanon's entropy measure, the average information of a set of events
[32]. In image processing, an event is the intensity of a pixel and an entire image is a set of events. Thus, according to Shanon's entropy measure, the average information of a set of events  with respective probabilities
with respective probabilities  is given by
is given by

MI gives a quantitative measure of the amount of information one set of events contains about another. Given two sets of events  and
and  , with respective probabilities
, with respective probabilities  and
and  , their MI is given by
, their MI is given by

which is the relative entropy between the joint distribution,  , and the product of marginal distributions
, and the product of marginal distributions  and
and  .
.
If we denote by  the utilities of the events in
the utilities of the events in  , the quantitative-qualitative measure of information of
, the quantitative-qualitative measure of information of  is defined as
is defined as

where the utility  can be any nonnegative real number.
can be any nonnegative real number.
Thus, it follows that the quantitative-qualitative measure of mutual information can be defined as

where  is the joint utility of the events
is the joint utility of the events  and
and  .
.
2.3. Saliency-Based Registration
QMI gives a measure of the amount of information one image contains about the other taking into account both intensity and saliency (utility) information. By maximizing the QMI of the two images to be registered, the optimal transformation parameters can be determined. Given a reference image  and a floating image
and a floating image  , we denote by
, we denote by  and
and  their respective pixel intensities. The goal of the registration procedure is to determine a transformation
their respective pixel intensities. The goal of the registration procedure is to determine a transformation  such that QMI, as given by (7), of the transformed floating image
such that QMI, as given by (7), of the transformed floating image  and the reference image
and the reference image  is maximum.
is maximum.

where  is the joint utility of the distribution of the images. The optimal transformation
is the joint utility of the distribution of the images. The optimal transformation  is,
is,

Joint Utility
The joint utility of an intensity pair can be defined in the following manner. Denoting the intensity and utility of a voxel in image  as
as  and
and  , respectively, and their counterparts in image
, respectively, and their counterparts in image  as
as  and
and  , the joint utility of intensity pair
, the joint utility of intensity pair  and
and  can be defined as
can be defined as

where the summation is over all pairs of pixels with intensity values  ;
;  and
and  are the voxels under consideration. We use the multiplication operator to consider the joint occurrence of utility values. For example, to calculate the joint utility of intensity pair (128,58), we find all the pairs of points
are the voxels under consideration. We use the multiplication operator to consider the joint occurrence of utility values. For example, to calculate the joint utility of intensity pair (128,58), we find all the pairs of points  such that all points in image
such that all points in image  have intensity
have intensity  and the corresponding points in image
and the corresponding points in image  has intensity
has intensity  . The joint utility is determined by multiplying the saliency values for a pair of points and summing over all such pairs. A normalized saliency map is used so that the most salient regions in two images have an equal importance of
. The joint utility is determined by multiplying the saliency values for a pair of points and summing over all such pairs. A normalized saliency map is used so that the most salient regions in two images have an equal importance of  . However, the joint utility value can exceed
. However, the joint utility value can exceed  as it reflects the joint importance of intensity pairs and not just individual utility values.
as it reflects the joint importance of intensity pairs and not just individual utility values.
2.4. Optimization
The most accurate optimization results are obtained by an exhaustive search for all combinations of different parameters. But it is not practical as it involves a lot of computations. There are many fast optimization algorithms in literature that make use of heuristics to speed up optimization [33]. Although such methods are fast they may not always give the global optimum as there is the possibility of getting trapped in a local optima. Therefore multiresolution search procedures are used where the parameters are first optimized over a coarse scale followed by a search on subsequent finer scales. However, we find that first finding the optimal rotation parameters and keeping it fixed, as described in [33] leads to errors in subsequent optimization steps when the rotation estimate is flawed. To address this problem, we adopt a different approach based on Powell's optimization routine [34] as described below:
-
(1)
The original image is subsampled to three coarser levels.
 indicates the original image;
indicates the original image; 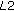 indicates a subsampling factor of
indicates a subsampling factor of 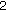 ,
,  indicates a factor of
indicates a factor of  , and
, and  indicates a subsampling factor of
indicates a subsampling factor of  .
. -
(2)
At
 , we perform an exhaustive search individually for each DOF and the optimal parameters are used to transform the image. The search range is
, we perform an exhaustive search individually for each DOF and the optimal parameters are used to transform the image. The search range is  voxels for translation along
voxels for translation along  -,
-,  -,
-,  -axis (
-axis ( ) and
) and  degree for rotation about
degree for rotation about  -,
-, 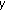 -,
-,  -axis (
-axis (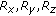 ).
). -
(3)
The registration parameters are interpolated which act as starting points for
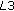 . The DOFs are individually optimized in two passes: first, rotation parameters over a search range of
. The DOFs are individually optimized in two passes: first, rotation parameters over a search range of 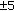 degrees and then
degrees and then 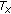 ,
, 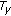 , and
, and  with search ranges of
with search ranges of  5,
5,  5, and
5, and  2 voxels. The optimal parameters are used to transform the volume and a second pass with the same sequence of steps is performed. The volume is transformed only if the parameters from the second pass indicate a better match than the parameters from first pass
2 voxels. The optimal parameters are used to transform the volume and a second pass with the same sequence of steps is performed. The volume is transformed only if the parameters from the second pass indicate a better match than the parameters from first pass -
(4)
The same process as step
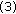 is repeated at a finer resolution level
is repeated at a finer resolution level 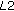 of the image.
of the image. -
(5)
The parameters from
 are interpolated to
are interpolated to  and an exhaustive search is carried out for
and an exhaustive search is carried out for  (
( 3 degrees),
3 degrees), 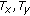 (
( 5 voxels) and
5 voxels) and  (
( 2 voxels).
2 voxels). -
(6)
The final parameters are used to get the registerd image.
The above optimization scheme proves to be robust as we pick the DOF to be optimized at random and repeat the entire scheme.
2.4.1. Results for Derivative-Based Optimizer
The Powell's optimization routine that we adopt is highly suitable for cost functions whose derivatives are not available and the computation cost is prohibitive. It works by evaluating candidate solutions in the parameter space over straight lines, that is, linear combinations of parameters. Such combinations require a bracketing of the minimum before the optimization can be started [34]. As a result, several necessary criterion estimations have to be performed which is inefficient when using a multiresolution strategy. Thévenaz et al. in [35] propose an optimization method based on the derivative of the similarity measure that makes better use of a multiresolution optimization setup.
The work in [35] uses MI as a similarity metric for rigid registration of natural and medical images. Mutual information is calculated using a Taylor expansion and B-Spline Parzen window functions. This facilitates easy computation of its derivatives for optimization purposes. Let  be the floating image and
be the floating image and  be the reference image defined on a continuous domain
be the reference image defined on a continuous domain  . Coordinates
. Coordinates  are samples of
are samples of  and the discrete set of these samples is denoted as
and the discrete set of these samples is denoted as  . Let
. Let  be a geometric transformation with parameters
be a geometric transformation with parameters  . Let
. Let  and
and  be discrete sets of intensities associated with
be discrete sets of intensities associated with  and
and  , respectively and
, respectively and  a separable B-spline based Parzen window. The joint discrete Parzen histogram is defined as
a separable B-spline based Parzen window. The joint discrete Parzen histogram is defined as

where  ,
,  , and
, and  is related to card(
is related to card( ) and
) and  to card(
to card( ). The contribution to the joint histogram of a single pair of pixels with intensities (
). The contribution to the joint histogram of a single pair of pixels with intensities ( ) is distributed over several discrete bins
) is distributed over several discrete bins  ) by the window function
) by the window function  . This joint histogram is proportional to the discrete Parzen probability
. This joint histogram is proportional to the discrete Parzen probability  given by
given by

where the normalization factor is

The marginal probabilities are given by

The utility measure is defined as the sum of product of saliency values of cooccurring intensity pairs. Equation (9) can be written as

where  and
and  are the saliency values of the reference and floating images.
are the saliency values of the reference and floating images.  denotes the cooccurring intensity pairs
denotes the cooccurring intensity pairs  and
and  . The utility measure is treated as a constant although it is dependent upon the cooccurring intensity pairs of
. The utility measure is treated as a constant although it is dependent upon the cooccurring intensity pairs of  and
and  . This is achieved by actually transforming the original saliency map of
. This is achieved by actually transforming the original saliency map of  according to the transformation,
according to the transformation,  , incurring a minor additional computational cost. Parzen windows is not used because the joint utility histogram is not a distribution of saliency values but the sum of the product of saliency values of cooccurring intensity pairs.
, incurring a minor additional computational cost. Parzen windows is not used because the joint utility histogram is not a distribution of saliency values but the sum of the product of saliency values of cooccurring intensity pairs.
The QMI between  and the transformed
and the transformed  is given by
is given by

The optimal registration parameter, given by  , is one which gives minimum value of
, is one which gives minimum value of  between the transformed test image
between the transformed test image  and
and  . The Taylor series expansion of (15) is given by
. The Taylor series expansion of (15) is given by

The gradient of  is given by
is given by

To compute the QMI value at different transformations we also calculate the second derivative of  as its Hessian
as its Hessian  . We refer the reader to [35] for details regarding calculation of
. We refer the reader to [35] for details regarding calculation of  and derivative of the joint probability distribution, that is,
and derivative of the joint probability distribution, that is,  in (17). Note that the utility is always treated as a constant, and as shown in (17), does not change the essence of the way derivatives of the cost functions are calculated.
in (17). Note that the utility is always treated as a constant, and as shown in (17), does not change the essence of the way derivatives of the cost functions are calculated.
A derivative-based cost function makes the method quite sensitive to the initial search parameters and their wrong choice may even lead to nonconvergence. Therefore, a multiresolution framework is used to get good candidate parameters from the first step. A  level image pyramid is created with the fourth level denoting the coarsest resolution. The parameters from the coarsest level are used to find the optimal parameters at finer levels by using the derivative of mutual information. This results in a significant reduction of computation time as compared to Powell's method where greater number of parameters need to be evaluated.
level image pyramid is created with the fourth level denoting the coarsest resolution. The parameters from the coarsest level are used to find the optimal parameters at finer levels by using the derivative of mutual information. This results in a significant reduction of computation time as compared to Powell's method where greater number of parameters need to be evaluated.
The transformation parameters are updated as a result of the minimization of the cost function. Two popular optimization methods are the steepest-gradient descent method and Newton method. The steepest-gradient descent algorithm is described as

Although its local convergence is guaranteed, it may be very slow. A key problem is determining the appropriate scaling diagonal matrix  . The Newton method is described as
. The Newton method is described as

Although the Newton method's convergence is not guaranteed, it is extremely efficient when the criterion is locally quadratic. To combine the advantages of the above two methods, the Marquardt-Levenburg strategy is used. A modified Hessian  , where the off-diagonal entries of
, where the off-diagonal entries of  is retained and its diagonal entries multiplied by a factor
is retained and its diagonal entries multiplied by a factor  , is defined as
, is defined as

where  is the Kroneckor function and
is the Kroneckor function and  is a tuning factor that represents the compromise between the gradient and Newton method. Thus
is a tuning factor that represents the compromise between the gradient and Newton method. Thus

Details of derivation of the different equations can be found in [35]. The optimization routine from the insight registration and segmentation toolkit (ITK) [36] was used. Each image was decomposed to  resolutions (similar to the scheme using Powell method) and registered using
resolutions (similar to the scheme using Powell method) and registered using  ,
,  , and
, and  by Thévenaz's optimization framework. To calculate the joint utility measure, the saliency maps of
by Thévenaz's optimization framework. To calculate the joint utility measure, the saliency maps of  (
( ) and
) and  (
( ) are calculated and for every parameter,
) are calculated and for every parameter,  is transformed to get the new map
is transformed to get the new map  .
.  and
and  are used to calculate the joint utility measure at every step.
are used to calculate the joint utility measure at every step.
Although the computation time is significantly lower than Powell's method the registration results are sensitive to the initial conditions. If the optimal parameters determined from the coarsest image resolution is far away from the actual transformation parameters then it is highly unlikely that Thevenaz's scheme will converge at the right solution. This problem is particularly acute when no multiresolution strategy is used. In that case, Powell's method is markedly superior. In a multiresolution setup when the initial conditions are good, Thevenaz's method converges in less time as compared to Powell's method with significantly less number of evaluations, but similar accuracy. Thevenaz's method can stop at any time and simultaneously optimizes all parameters from the first criterion resulting in a reduction in the number of criterion evaluations.
A clear advantage of the Powell method is its robustness. This calls for the use of a derivative-based global optimization method using Powell's method in the coarsest stage. Subsequently, Thevenaz's method can be used in the finer stages for faster convergence. The registration accuracy using such an approach is consistently closer to the values reported in Table 2. Without using Powell's method in the coarsest stage, the registration error for many of the volume pairs is greater than using Powell's method.
3. Experiments
3.1. Subjects
The volumes were obtained from  healthy volunteers (
healthy volunteers ( women and
women and  men,
men,  years) and
years) and  patients (
patients ( women and
women and  men,
men,  years) with renal insufficiency manifested by serum creatinine
years) with renal insufficiency manifested by serum creatinine  mg/dl (
mg/dl ( mg/dl). Written informed consent was obtained from all subjects. All the
mg/dl). Written informed consent was obtained from all subjects. All the  datasets were used for testing. Note that every dataset comprised of
datasets were used for testing. Note that every dataset comprised of  kidneys. The results for each dataset are the average errors for tests on both kidneys.
kidneys. The results for each dataset are the average errors for tests on both kidneys.
3.2. MRI Acquisition Protocol
Dynamic MRI was performed on a  T system (Avanto; Siemens, Erlangen, Germany) with a maximum slew rate of
T system (Avanto; Siemens, Erlangen, Germany) with a maximum slew rate of  T/m/s, maximum gradient strength of
T/m/s, maximum gradient strength of  mT/m, and a torso phased-array coil.
mT/m, and a torso phased-array coil.  D
D  -weighted spoiled gradient-echo imaging was performed in the oblique coronal orientation to include the abdominal aorta and both kidneys. The following parameters were used:
-weighted spoiled gradient-echo imaging was performed in the oblique coronal orientation to include the abdominal aorta and both kidneys. The following parameters were used:  ms,
ms,  ms, flip
ms, flip  ,
,  ,
,  ,
,  Hz/voxel, volume acquisition
Hz/voxel, volume acquisition  s. The
s. The  original 5-mm coronal partitions were interpolated to
original 5-mm coronal partitions were interpolated to  mm slices.
mm slices.
Five unenhanced acquisitions were performed during a single breath-hold. A  -ml bolus of Gd-DTPA(Magnevist; Berlex laboratories, Wyne, NJ, USA) was then injected, followed by
-ml bolus of Gd-DTPA(Magnevist; Berlex laboratories, Wyne, NJ, USA) was then injected, followed by  ml of saline, both at
ml of saline, both at  ml/s. Over
ml/s. Over  min,
min,  D volumes were acquired using a variable sampling schedule:
D volumes were acquired using a variable sampling schedule:  sets acquired at
sets acquired at  s intervals, followed by
s intervals, followed by  sets at intervals of
sets at intervals of  s, followed by
s, followed by  at
at  s intervals, and ending with
s intervals, and ending with  sets over one minute intervals. The first
sets over one minute intervals. The first  sets were attempted to be acquired within a single breath-hold. Before each subsequent acquisition, the patients were instructed to suspend respiration at end-expiration. Oxygen via nasal cannula was routinely offered to the patients before the exam to facilitate breath-holding. For image processing, all
sets were attempted to be acquired within a single breath-hold. Before each subsequent acquisition, the patients were instructed to suspend respiration at end-expiration. Oxygen via nasal cannula was routinely offered to the patients before the exam to facilitate breath-holding. For image processing, all  D volumes (
D volumes ( acquired before and
acquired before and  after contrast agent injection) were evaluated.
after contrast agent injection) were evaluated.
3.3. Registration Procedure
Two volumes of interest (VOI), each encompassing a kidney were selected from each volume. We test the effectiveness of our algorithm by registering the entire VOI sequence of each patient to a reference VOI. Each kidney had a different reference VOI. For different cases, different pre- and postcontrast VOIs were chosen as reference. Saliency maps were calculated for each slice of a VOI and saliency information from these maps was used to define the utility measure of each voxel. For every reference-floating VOI pair, the floating VOI is transformed according to the scheme outlined in Section 2.4 and for each candidate transformation parameter, the QMI-based similarity measure (6) is calculated. The candidate transformation parameters that give the maximum value of QMI are used to get the final transformation. We evaluate the performance of our algorithm using the ground truth for registration provided by a clinical expert.
To check for the robustness and effectiveness of the proposed similarity measure we determined its characteristics with change in transformation parameters. For this purpose, rotation and translation motion was simulated on the datasets. In an attempt to recover the applied motion the value of the similarity measure at different candidate transformation parameters was calculated. The characteristics thus obtained gave an idea of the suitability of the similarity measure for registering DCE images. The robustness of different similarity measures was determined by first misaligning the images by different degrees of known translation and rotation. Three different similarity measures were used in the tests, namely, normalized mutual information ( ) [37], QMI in [20] (
) [37], QMI in [20] ( ), and our proposed method (
), and our proposed method ( ). NMI is a popular similarity measure used for registering multimodal images; that is, images of the same organ but from different modalities such as MR and CT, and its performance can help us gauge the effectiveness of our method.
). NMI is a popular similarity measure used for registering multimodal images; that is, images of the same organ but from different modalities such as MR and CT, and its performance can help us gauge the effectiveness of our method.
4. Results
We present results for different experiments that show the importance of using saliency in registering DCE images of the kidney.  datasets comprising of
datasets comprising of 
 D volumes were used and each volume consists of
D volumes were used and each volume consists of  slices. Manual registration parameters by experts were available for each dataset facilitating performance comparison. First, we present proof of the suitability of saliency for registering contrast enhanced images. Then we show properties of the different similarity measures with respect to registration. These sets of results are similar to those presented in [20]. They highlight the fact although
slices. Manual registration parameters by experts were available for each dataset facilitating performance comparison. First, we present proof of the suitability of saliency for registering contrast enhanced images. Then we show properties of the different similarity measures with respect to registration. These sets of results are similar to those presented in [20]. They highlight the fact although  was a good measure to register brain MR images,
was a good measure to register brain MR images,  shows better performance than
shows better performance than  in registering renal perfusion images. This is reflected in the properties of the different similarity measures. Finally, we present registration results of real patient datasets and compare relative performance of different similarity measures with respect to manual registration parameters.
in registering renal perfusion images. This is reflected in the properties of the different similarity measures. Finally, we present registration results of real patient datasets and compare relative performance of different similarity measures with respect to manual registration parameters.
To calculate the registration error due to simulated motion we adopt the following steps. Let  be the value of simulated motion (translation or rotation) parameter and
be the value of simulated motion (translation or rotation) parameter and  be the value of recovered motion parameter. The error is equal to
be the value of recovered motion parameter. The error is equal to  and the error as a percentage of the simulated motion is given as
and the error as a percentage of the simulated motion is given as

For simulated motion, registration was deemed to be accurate if  .
.
4.1. Saliency Maps for Pre- and Postcontrast Enhanced Images
In DCE images, the intensity of the region of interest changes with time due to the flow of contrast agent. In Figure 1, we show the target image and images from different stages of contrast enhancement along with their respective saliency maps. Zero mean Gaussian noise of different variances has been added to the displayed images. Although there is progressive contrast enhancement of the kidney in addition to the noise, we observe that the saliency maps are very similar. This can be attributed to the fact that the regular structure of the kidney with its edges dominates over the effect of intensity in determining saliency. The intensities of the images ranged from  to
to  and the variance of added noise ranged from
and the variance of added noise ranged from  to
to  . The variance of the images from a typical dataset varied from
. The variance of the images from a typical dataset varied from  to
to  . The image intensity values were all normalized between
. The image intensity values were all normalized between  and
and  . As long as the variance of added noise is less than
. As long as the variance of added noise is less than  the saliency maps are nearly identical. Beyond a variance value of
the saliency maps are nearly identical. Beyond a variance value of  it is difficult to even visually identify the kidney from the images. The simulated motion studies were carried out for zero mean Gaussian noise with different variances.
it is difficult to even visually identify the kidney from the images. The simulated motion studies were carried out for zero mean Gaussian noise with different variances.
Saliency maps of contrast enhanced image sequence. (a)–(d) show images from different stages of contrast enhancement with added noise. The variance of noise added was .02, .05, .08, and .1. (a) is the reference image to which all images are registered. (e)–(h) show the respective saliency maps; (i) colorbar for the saliency maps. The saliency maps are seen to be similar. Color images are for illustration purposes. In actual experiments gray scale images were used.
To demonstrate that the saliency value in DCE images is indeed constant, we plot the average saliency value over pixel windows from images of different stages of contrast enhancement. In Figure 2, we show the mean saliency value of patches of sizes  ,
,  , and
, and  from different areas of the kidney, with best results for the
from different areas of the kidney, with best results for the  patch. The mean saliency value of the background is zero even in precontrast images because the kidney due to its well defined structure and edges is more salient than the background. We take two different patches from the cortex to highlight that different areas of the cortex have different saliency values which change little over contrast enhancement. To achieve registration the kidney need not be the most salient region as long as it has a nearly constant saliency profile over the course of contrast enhancement. The maps show saliency to be a measure that is constant over contrast enhancement and it is desirable to exploit this information for registration of DCE images.
patch. The mean saliency value of the background is zero even in precontrast images because the kidney due to its well defined structure and edges is more salient than the background. We take two different patches from the cortex to highlight that different areas of the cortex have different saliency values which change little over contrast enhancement. To achieve registration the kidney need not be the most salient region as long as it has a nearly constant saliency profile over the course of contrast enhancement. The maps show saliency to be a measure that is constant over contrast enhancement and it is desirable to exploit this information for registration of DCE images.
4.2. Registration Functions
A similarity measure for two images should have the following desirable properties: (a) it should be smooth and convex with respect to the transformation parameters; (b) the global optimum of the registration function should be close to the correct transformation that aligns two images perfectly; (c) the capture range should be as large as possible; and (d) the number of local maxima should remain at a minimum. We can determine the registration function of  by calculating its value under different transformations.
by calculating its value under different transformations.
In Figure 3, we show the registration functions for different translation and rotation ranges corresponding to  different similarity measures namely
different similarity measures namely  ,
,  and
and  . Motion was simulated on randomly chosen images belonging to either the pre- or postcontrast enhancement stage. The motion simulated image was the floating image which was registered to the original image without any motion. Zero mean Gaussian noise of different variance (
. Motion was simulated on randomly chosen images belonging to either the pre- or postcontrast enhancement stage. The motion simulated image was the floating image which was registered to the original image without any motion. Zero mean Gaussian noise of different variance ( ) was added and the values of the similarity measure for different candidate transformation parameters calculated. The known transformations were randomly chosen from a uniform distribution of
) was added and the values of the similarity measure for different candidate transformation parameters calculated. The known transformations were randomly chosen from a uniform distribution of  mm for translation along along
mm for translation along along  - and
- and  - axis (
- axis ( and
and  ) and
) and  mm for translation along
mm for translation along  axis (
axis ( ). For rotation the corresponding ranges were
). For rotation the corresponding ranges were  degrees (
degrees ( ). Thus in all figures, the
). Thus in all figures, the  -axis shows the relative error between the actual transformation and candidate transformation. The plots for all the
-axis shows the relative error between the actual transformation and candidate transformation. The plots for all the  similarity measures show a distinct global maximum. However, for
similarity measures show a distinct global maximum. However, for  and
and  , the plots are a lot smoother than those for
, the plots are a lot smoother than those for  . Using
. Using  produces many local minimum, which is an undesirable attribute in the registration task. From Figure 3, we see that, besides being noisy the plot for
produces many local minimum, which is an undesirable attribute in the registration task. From Figure 3, we see that, besides being noisy the plot for  is also inaccurate as the global maximum is at a nonzero relative error. This inaccuracy is evident for
is also inaccurate as the global maximum is at a nonzero relative error. This inaccuracy is evident for  also. However,
also. However,  is accurate for these cases where the global maximum is found for zero-relative error and the measure varies in a smooth manner.
is accurate for these cases where the global maximum is found for zero-relative error and the measure varies in a smooth manner.
Plots showing variation of different similarity measures when registering pre- or postcontrast images. First column is for NMI, second column for QMI1, and third column for QMI2. First row shows the variation for rotation parameters about x-axis while second column shows variation for translation along x-axis. The variance of added noise was 0.08. x-axis of the plots shows relative error between actual and candidate transformations while y-axis shows value of similarity measure.
It is to be kept in mind that the profile for the different similarity measures in Figure 3 is for  . For
. For  the performance of
the performance of  and
and  is comparable, that is, the maximum of the similarity measures is mostly at zero relative error. When
is comparable, that is, the maximum of the similarity measures is mostly at zero relative error. When  ,
,  shows a superior performance demonstrating the efficacy of a neurobiology based saliency model. Similarly, for
shows a superior performance demonstrating the efficacy of a neurobiology based saliency model. Similarly, for  , performance of
, performance of  is comparable to the other two saliency measures but degrades once
is comparable to the other two saliency measures but degrades once  . The corresponding threshold for
. The corresponding threshold for  is
is  . The accuracy (from (22)) in recovering the correct transformation was
. The accuracy (from (22)) in recovering the correct transformation was  for
for  ,
,  for
for  , and
, and  for
for  .
.
In the previous cases motion was simulated on a pre- or postcontrast image and the simulated image is registered to the original image. To test for the effectiveness of registering precontrast images to postcontrast images (or vice-versa) we carried out the following experiments. A pair of images, one each from pre- and postcontrast stages, were selected such that they had very little motion between them as confirmed by observers and manual registration parameters. Rotation and translation motion were individually simulated on one of the images which served as the floating image. The floating image was then registered to the other image which was the reference image. The similarity measure values were determined for each candidate transformation parameter. Figure 4 shows a case where  fails to get the actual transformation, a shortcoming overcome by
fails to get the actual transformation, a shortcoming overcome by  .
.
Plots showing variation of different similarity measures when registering pre- and postcontrast images: (a) NMI; (b) QMI1; (c) QMI2. The plots show results for Ty (translation along y-axis). x-axis of the plots shows relative error between actual and candidate transformations while y-axis shows value of similarity measure.
In most cases,  was unable to detect the right transformation between a pair of pre- and postcontrast images. Figure 4(a) shows two maxima for
was unable to detect the right transformation between a pair of pre- and postcontrast images. Figure 4(a) shows two maxima for  at nonzero error, in addition to being noisy. Such characteristics are undesirable for registration. For
at nonzero error, in addition to being noisy. Such characteristics are undesirable for registration. For  although there are no multiple maxima, it is at nonzero relative error. It is observed that even though
although there are no multiple maxima, it is at nonzero relative error. It is observed that even though  performs better than
performs better than  due to use of saliency,
due to use of saliency,  outperforms both of them.
outperforms both of them.
The accuracy rate for registering DCE images was  for
for  ,
,  for
for  , and
, and  for
for  . The low registration accuracy of
. The low registration accuracy of  makes it imperative that we investigate the reason behind it. We shall do this with the help of an example.
makes it imperative that we investigate the reason behind it. We shall do this with the help of an example.
Let us consider a  image patch with intensity values as shown in Figure 5(a). With its different intensity values at different locations, it is similar to an image showing the kidney and the background, as shown in Figure 5(b). The pixels with intensity value
image patch with intensity values as shown in Figure 5(a). With its different intensity values at different locations, it is similar to an image showing the kidney and the background, as shown in Figure 5(b). The pixels with intensity value  correspond to the kidney and the pixels with intensity value
correspond to the kidney and the pixels with intensity value  are the background pixels. In the precontrast stage, the background is generally brighter than the kidney. With progressive wash in of contrast agent the intensity of the kidney increases. Figure 5(c) shows the change in intensity where some kidney pixels now have intensity value
are the background pixels. In the precontrast stage, the background is generally brighter than the kidney. With progressive wash in of contrast agent the intensity of the kidney increases. Figure 5(c) shows the change in intensity where some kidney pixels now have intensity value  . It is similar to progressive contrast enhancement where certain kidney tissues first exhibit intensity increase followed by the rest of the kidney. The corresponding patch is shown in Figure 5(d).
. It is similar to progressive contrast enhancement where certain kidney tissues first exhibit intensity increase followed by the rest of the kidney. The corresponding patch is shown in Figure 5(d).
We want to register the central  patch in image Figure 5(a) similar to a region of interest, the values of which are highlighted in bold. The intensity values of Figure 5(c) only indicate contrast enhancement without any kind of motion. For an ideal registration, the central patch of Figure 5(a) should give maximum value of NMI (from [37]) for the
patch in image Figure 5(a) similar to a region of interest, the values of which are highlighted in bold. The intensity values of Figure 5(c) only indicate contrast enhancement without any kind of motion. For an ideal registration, the central patch of Figure 5(a) should give maximum value of NMI (from [37]) for the  central patch of Figure 5(c). The
central patch of Figure 5(c). The  value in this case is
value in this case is  . However, the maximum value is obtained for the image patch shown in bold in Figure 5(c) (
. However, the maximum value is obtained for the image patch shown in bold in Figure 5(c) ( ), which corresponds to a displacement of one pixel to the left and one pixel down. Although there is no translation motion, the maximum value of
), which corresponds to a displacement of one pixel to the left and one pixel down. Although there is no translation motion, the maximum value of  is obtained for parameters corresponding to such motion. The intensity change in the image patch is quite similar to what we observe for DCE images of the kidney. Consequently, the maximum value is obtained at nonzero relative error and more than one maximum is observed for many cases. Thus, there are a significantly high number of misregistrations using
is obtained for parameters corresponding to such motion. The intensity change in the image patch is quite similar to what we observe for DCE images of the kidney. Consequently, the maximum value is obtained at nonzero relative error and more than one maximum is observed for many cases. Thus, there are a significantly high number of misregistrations using  which contributes to its high error rate.
which contributes to its high error rate.
From these observations, we infer that  performs well when a particular intensity in the first image (
performs well when a particular intensity in the first image ( ) is mapped to a distinct intensity in the second image (
) is mapped to a distinct intensity in the second image ( ). If two intensity values in
). If two intensity values in  are mapped to the same intensity value in
are mapped to the same intensity value in  or vice-versa then
or vice-versa then  leads to poor matching. Due to contrast enhancement, it is very common to find more than one intensity mapped to a single intensity. Consequently,
leads to poor matching. Due to contrast enhancement, it is very common to find more than one intensity mapped to a single intensity. Consequently,  -based registration is prone to error which is reflected in the error measures.
-based registration is prone to error which is reflected in the error measures.
4.3. Robustness of Registration
A robust registration algorithm should be able to recover the true transformation between two images even if the initial misalignment between them is very large. We evaluate the robustness of  ,
,  , and
, and  under various amounts of initial misalignment between two kidney MR images. Four sets of tests were performed where the degree of initial misaligned rotation angles were randomly picked from four different rotation ranges, that is,
under various amounts of initial misalignment between two kidney MR images. Four sets of tests were performed where the degree of initial misaligned rotation angles were randomly picked from four different rotation ranges, that is,  ,
,  ,
,  , and
, and  degrees. Similarly, misalignment was simulated for translational motion in the
degrees. Similarly, misalignment was simulated for translational motion in the  ,
,  , and
, and  directions. The misalignment values varied between
directions. The misalignment values varied between  ,
,  and
and  mm. For each misalignment range, we performed
mm. For each misalignment range, we performed  registrations between different pairs of images. Zero mean Gaussian noise of variance
registrations between different pairs of images. Zero mean Gaussian noise of variance  was added to the images.
was added to the images.
The number of successful registrations for each type of similarity measure is shown in Figure 6. Figure 6(a) shows the numbers for rotation misalignment, and Figure 6(b) shows results for translation misalignment. All the image pairs were from the same stage of contrast enhancement, either precontrast or postcontrast stage. For a small misalignment range the degree of misregistration is very low for all the similarity measures ( for all similarity measures when misalignment is
for all similarity measures when misalignment is  ). As the misalignment range increases, the number of successful registration decreases for all similarity measures but is still high for saliency-based similarity measures, especially
). As the misalignment range increases, the number of successful registration decreases for all similarity measures but is still high for saliency-based similarity measures, especially  . The robustness of
. The robustness of  reduces drastically with an increase in misalignment range while for
reduces drastically with an increase in misalignment range while for  higher misalignment ranges also affect its performance. However, the performance of
higher misalignment ranges also affect its performance. However, the performance of  in particular is not much affected. For all cases of rotation misalignment, the accuracy of registration is a minimum of
in particular is not much affected. For all cases of rotation misalignment, the accuracy of registration is a minimum of  for
for  . From Figure 6(b), we can draw the same conclusions for translational misalignment.
. From Figure 6(b), we can draw the same conclusions for translational misalignment.
In Figure 7 we present results for similar experiments but in this case the source-target image pair comprised of a pre- and postcontrast image. Similar to the experiments in Section 4.2 for contrast enhanced images, we chose pairs of images that had very little translation or rotation motion between them (a fact confirmed by observers and manual registration parameters). From the registration accuracies in Figures 7(a) and 7(b), we see that for registering contrast enhanced image pairs,  shows inferior performance compared to saliency-based similarity measures as it is unable to account for intensity changes due to contrast enhancement. For a small misalignment range, a large number of inaccurate registrations were observed. Compared to Figure 6, we observe that in Figure 7 there is not a large difference in results for
shows inferior performance compared to saliency-based similarity measures as it is unable to account for intensity changes due to contrast enhancement. For a small misalignment range, a large number of inaccurate registrations were observed. Compared to Figure 6, we observe that in Figure 7 there is not a large difference in results for  and
and  .
.
The average translation error along the  axes was (
axes was ( ) mm for
) mm for  , (
, ( ) mm for
) mm for  , and (
, and ( ) mm for
) mm for  . The average rotation errors were (
. The average rotation errors were ( ) degrees for
) degrees for  , (
, ( ) degrees for
) degrees for  and (
and ( ) degrees for
) degrees for  . The maximum errors for simulated motion was
. The maximum errors for simulated motion was  mm and
mm and  for
for  ,
,  mm and
mm and  for
for  , and
, and  mm and
mm and  for
for  .
.
From Figures 6 and 7, we infer that as long as there is no drastic intensity change between a pair of images,  gives good performance up to a certain misalignment range. But with intensity change due to contrast enhancement
gives good performance up to a certain misalignment range. But with intensity change due to contrast enhancement  's performance drops. To get an average error measure, we simulated misalignment in all images at different noise levels except the first image of the sequence. The known simulated motion was in the range of
's performance drops. To get an average error measure, we simulated misalignment in all images at different noise levels except the first image of the sequence. The known simulated motion was in the range of  mm for translation and
mm for translation and  degrees for rotation. The manual registration parameters were with respect to the first image which serves as the reference image. The new displacement is equal to the sum of simulated displacement and original displacement. The floating image was registered to the reference image and the registration error calculated according to the following steps. Let
degrees for rotation. The manual registration parameters were with respect to the first image which serves as the reference image. The new displacement is equal to the sum of simulated displacement and original displacement. The floating image was registered to the reference image and the registration error calculated according to the following steps. Let  be the recovered motion,
be the recovered motion,  be the simulated motion and
be the simulated motion and  be the original motion from manual registration parameters. The error in registration is given by
be the original motion from manual registration parameters. The error in registration is given by

where  is the registration error. The average registration error for different levels of noise is given in Table 1. Similarly, to get an idea of the comparative performance of the three similarity measures, we also calculate their individual registration accuracy percentages for simulated motion. Registration was considered accurate if the error (from (23)) was less than
is the registration error. The average registration error for different levels of noise is given in Table 1. Similarly, to get an idea of the comparative performance of the three similarity measures, we also calculate their individual registration accuracy percentages for simulated motion. Registration was considered accurate if the error (from (23)) was less than  and the results are shown in Table 1.
and the results are shown in Table 1.
 -,
-,  -,
-,  -axis.
-axis. is normalized mutual information.
is normalized mutual information.  is the measure in [20] using scale-space maps.
is the measure in [20] using scale-space maps.  is our approach using the neurobiology-based saliency model. All values are in units of mm.
is our approach using the neurobiology-based saliency model. All values are in units of mm.4.4. Registration Accuracy for Real Patient Data
The registration accuracy of the different similarity measures is determined by registering real patient datasets of DCE kidney images. The reference image was the first from the image sequence as the manual registration parameters are with respect to the first image. We compare the error between recovered transformation and the transformation parameters as determined by manual correction of an expert. In Figure 8, we show reference-floating image pairs along with the difference images before and after registration. The first and second columns show the reference image followed by the floating image and the difference image before registration is shown in the third column. The three subsequent columns show the difference images after registration using  ,
,  , and
, and  , respectively. The first
, respectively. The first  rows show cases where one image of the reference-floating image pair was from the precontrast stage and the other belonged to the postcontrast stage. Here the performance of
rows show cases where one image of the reference-floating image pair was from the precontrast stage and the other belonged to the postcontrast stage. Here the performance of  does not measure upto that of
does not measure upto that of  and
and  . The difference images after using
. The difference images after using  in registration show a lot of artifacts which have been improved upon by the saliency based measures. Also, we find
in registration show a lot of artifacts which have been improved upon by the saliency based measures. Also, we find  to perform better than
to perform better than  in registering contrast enhanced images. Rows
in registering contrast enhanced images. Rows  and
and  show examples where the floating and reference images both belong to the precontrast or postcontrast stage. In such a scenario, the registration achieved by
show examples where the floating and reference images both belong to the precontrast or postcontrast stage. In such a scenario, the registration achieved by  is comparable to
is comparable to  and
and  although the saliency-based measures show better results. The performance of different similarity measures is summarized in Tables 2 and 3.
although the saliency-based measures show better results. The performance of different similarity measures is summarized in Tables 2 and 3.
 is normalized mutual information.
is normalized mutual information.  is the measure in [20] using scale-space maps.
is the measure in [20] using scale-space maps.  is our approach using the neurobiology-based saliency model. All values are in units of degrees.
is our approach using the neurobiology-based saliency model. All values are in units of degrees.Difference images highlighting performance of our registration algorithm. Columns 1–3 show reference image, floating image, and difference image before registration. Columns 4–6 show difference images after registration using NMI, QMI1, and QMI2, respectively. Rows 1 and 2 show pairs of images belonging to different stages of contrast enhancement. Rows 3 and 4 show images where the reference-floating image pair was from either pre- or postcontrast stage.
For all datasets,  shows a higher error measure compared to
shows a higher error measure compared to  and
and  . This can be attributed to the errors due to registering pre- and postcontrast image pairs. For
. This can be attributed to the errors due to registering pre- and postcontrast image pairs. For  , the maximum error was as high as
, the maximum error was as high as  mm for translation and
mm for translation and  degrees for rotation. Such a large error is not desirable, especially in medical image registration. For
degrees for rotation. Such a large error is not desirable, especially in medical image registration. For  the maximum error was
the maximum error was  mm and
mm and  degrees and the corresponding values for
degrees and the corresponding values for  were
were  mm and
mm and  degrees, respectively. Moreover, the average error values for
degrees, respectively. Moreover, the average error values for  were higher than that of
were higher than that of  and
and  . For translation along
. For translation along  -axis, there was no significant difference between error values of different similarity measures as there is hardly any motion along the
-axis, there was no significant difference between error values of different similarity measures as there is hardly any motion along the  -axis. For rotation, we see that the error values for
-axis. For rotation, we see that the error values for  - and
- and  -axis are all
-axis are all  because there is no rotation about these axes. Rotational motion is observed only about the
because there is no rotation about these axes. Rotational motion is observed only about the  -axis with the average error measures for
-axis with the average error measures for  much greater than those for
much greater than those for  and
and  .
.
4.5. Computation Time
The difference between our method and the one proposed in [20] is the choice of saliency models. While we use the saliency model of [22], Luan et al. use the scale-space method of [21]. The source code for both the methods is available from the websites of the respective authors. For a kidney image of dimension  , the average time taken to calculate the scale space map and identify salient regions was
, the average time taken to calculate the scale space map and identify salient regions was  seconds while the neurobiology based saliency map could be computed in
seconds while the neurobiology based saliency map could be computed in  seconds on average. The difference in computing saliency maps is not significant and in registering a large number of images by our method, the saving in computation time is a few seconds.
seconds on average. The difference in computing saliency maps is not significant and in registering a large number of images by our method, the saving in computation time is a few seconds.
Another difference from the method in [20] is an optimization scheme that incorporates a certain degree of randomness, thus reducing the chances of being trapped in a local minimum. This modification involves a marginally greater number of steps leading to a slight increase in computation time. While the average time taken by our method (inclusive of calculating saliency maps) is  s for registering a pair of volumes, the corresponding average time for the method in [20] was
s for registering a pair of volumes, the corresponding average time for the method in [20] was  s. By Thevenaz's method, the computation time reduces to
s. By Thevenaz's method, the computation time reduces to  s using
s using  and
and  s for
s for  .
.
5. Discussion and Conclusion
In this work, we have investigated a neurobiological model of visual saliency and its use in registering perfusion images. The motivation was to determine whether the HVS's ability to recognize and match images in presence of noise and contrast enhancement can be simulated by a computational model. We register MR kidney perfusion volumes because they exhibit rapid intensity change and the acquired datasets also have a significant amount of noise.
The neurobiology-based saliency model is used because it produces very similar saliency maps for a pair of images with intensity change between them and facilitates registration in the face of contrast enhancement. We do a comparative study of the effectiveness of different saliency models for registering renal perfusion images and find the neurobiology-based model to be better than scale-space maps.
Several factors contribute to the superior performance of the neurobiological model of saliency. There are certain inherent faults in the scale space method used in [20] to get saliency information. First, the change in intensity assigns different saliency values to corresponding voxels in an image pair. This is undesirable for registration. Second, there is the problem of the choice of an appropriate scale (neighborhood) for calculating the local entropy of a voxel. The scale which gives the maximum value of entropy is chosen as the best scale, thus making the procedure computationally intensive. Third, since it is an entropy-based method, noise can greatly affect the entropy value leading to erroneous results. Fourth, a scale-space saliency map of an image does not truly represent what is salient to the human eye. In the neurobiology model, the center-surround approach assigns the same saliency value to corresponding pixels in an image pair and a Gaussian pyramidal representation of the image eliminates the need for determining the optimal scale for each voxel. An important part of the model is the process of lateral inhibition that suppresses noise giving rise to a saliency map that has distinctly salient regions. Lastly, the neurobiology model has been used to predict human fixations in a scene and there is high degree of correlation between the predicted and actual fixations.
Our optimization technique also contributes to improved performance of our method. Instead of following a set pattern for optimizing the DOFs, we introduce a degree of randomness in the entire optimization scheme based on Powell's method. A  -level multiresolution approach was adopted where candidate transformation parameters for different DOFs were first calculated at the coarsest level and the solution propagated to finer levels. The optimization routine was repeated at the finer levels to get the final transformation. The sequence of DOFs optimized is random. By adopting this method the optimization scheme avoids being trapped in local optima and reachs the global optima, as determined by an exhaustive search, in most of the experiments. This approach also gives better performance than the optimization scheme outlined in [33]. We also use a derivative-based optimizer (Thévenaz's method) to determine the optimal registration parameters. If the starting point for the search is close to the actual optima ths method gives accurate results in significantly less time. An approach using Powell's method for search at the coarsest level followed by Thevenaz's method at finer levels gives registration accuracy close to what is obtained using Powell's method at all levels but in significantly lesser computation time.
-level multiresolution approach was adopted where candidate transformation parameters for different DOFs were first calculated at the coarsest level and the solution propagated to finer levels. The optimization routine was repeated at the finer levels to get the final transformation. The sequence of DOFs optimized is random. By adopting this method the optimization scheme avoids being trapped in local optima and reachs the global optima, as determined by an exhaustive search, in most of the experiments. This approach also gives better performance than the optimization scheme outlined in [33]. We also use a derivative-based optimizer (Thévenaz's method) to determine the optimal registration parameters. If the starting point for the search is close to the actual optima ths method gives accurate results in significantly less time. An approach using Powell's method for search at the coarsest level followed by Thevenaz's method at finer levels gives registration accuracy close to what is obtained using Powell's method at all levels but in significantly lesser computation time.
Thus, we conclude that the neurobiological model of saliency gives a fairly accurate working of the HVS-based on bottom-up cues alone. It is robust to varying degrees of noise and simulated motion. The original model in [22] uses color, intensity, and edge orientation as features in determining the saliency map. But, for our work, we use only intensity and edge orientation information since our datasets are in gray scale. The findings of our experiments provide a basis for investigating how saliency can be used in more challenging registration tasks and also in other computer vision applications like tracking.
References
Dufaux F, Konrad J: Efficient, robust, and fast global motion estimation for video coding. IEEE Transactions on Image Processing 2000,9(3):497-501. 10.1109/83.826785
Irani M, Peleg S: Motion analysis for image enhancement: resolution, occlusion, and transparency. Journal of Visual Communication and Image Representation 1993,4(4):324-335. 10.1006/jvci.1993.1030
Irani M, Anandan P, Hsu S: Mosaic based representations of video sequences and their applications. Proceedings of the 5th International Conference on Computer Vision, June 1995 605-611.
Hill DLG, Batchelor PG, Holden M, Hawkes DJ: Medical image registration. Physics in Medicine and Biology 2001,46(3):R1-R45. 10.1088/0031-9155/46/3/201
Lao Z, Shen D, Jawad A, Karacali B, Liu D, Melhem ER, Bryan RN, Davatzikos C: Automated segmentation of white matter lesions in 3D brain MR images, using multivariate pattern classification. Proceedings of the 3rd IEEE International Symposium on Biomedical Imaging, April 2006 307-310.
Song T, Lee VS, Rusinek H, Kaur M, Laine AF: Automatic 4-D registration in dynamic mr renography based on over-complete dyadic wavelet and Fourier transforms. Proceedings of the 8th International Conference on Medical Image Computing and Computer-Assisted Intervention (MICCAI '05), October 2005, Palm Springs, Calif, USA, Lecture Notes in Computer Science 3750: 205-213.
Hawkes DJ: Algorithms for radiological image registration and their clinical application. Journal of Anatomy 1998,193(3):347-361. 10.1046/j.1469-7580.1998.19330347.x
Viola P, Wells WM III: Alignment by maximization of mutual information. International Journal of Computer Vision 1997,24(2):137-154. 10.1023/A:1007958904918
Collignon A, Maes F, Delaere D, Vandermeulen D, Suetens P, Marchal G: Automated multimodality image registration based on information theory. Proceedings of the International Conference on Information Processing in Medical Imaging (IPMI '95), 1995 263-274.
Keller Y, Averbuch A, Israeli M: Pseudopolar-based estimation of large translations, rotations, and scalings in images. IEEE Transactions on Image Processing 2005,14(1):12-22.
Wolberg G, Zokai S: Robust image registration using log-polar transform. Proceedings of the International Conference on Image Processing (ICIP '00), September 2000, Vancouver, Canada 493-496.
Reddy BS, Chatterji BN: An FFT-based technique for translation, rotation, and scale-invariant image registration. IEEE Transactions on Image Processing 1996,5(8):1266-1271. 10.1109/83.506761
Lemieux L, Jagoe R, Fish DR, Kitchen ND, Thomas DGT: A patient-to-computed-tomography image registration method based on digitally reconstructed radiographs. Medical Physics 1994,21(11):1749-1760. 10.1118/1.597276
Keller Y, Averbuch A: A projection-based extension to phase correlation image alignment. Signal Processing 2007,87(1):124-133. 10.1016/j.sigpro.2006.04.013
Wong A, Fieguth P: Fast phase-based registration of multimodal image data. Signal Processing 2009,89(5):724-737. 10.1016/j.sigpro.2008.10.028
Shen D, Davatzikos C: HAMMER: hierarchical attribute matching mechanism for elastic registration. IEEE Transactions on Medical Imaging 2002,21(11):1421-1439. 10.1109/TMI.2002.803111
Giele ELW, De Priester JA, Blom JA, Den Boer JA, Van Engelshoven JMA, Hasman A, Geerlings M: Movement correction of the kidney in dynamic MRI scans using FFT phase difference movement detection. Journal of Magnetic Resonance Imaging 2001,14(6):741-749. 10.1002/jmri.10020
Gupta SN, Solaiyappan M, Beache GM, Arai AE, Foo TKF: Fast method for correcting image misregistration due to organ motion in time-series MRI data. Magnetic Resonance in Medicine 2003,49(3):506-514. 10.1002/mrm.10394
Sun Y, Jolly M-P, Moura JMF: Integrated registration of dynamic renal perfusion MR images. Proceedings of the International Conference on Image Processing (ICIP '04), October 2004, Singapore 1923-1926.
Luan H, Qi F, Xue Z, Chen L, Shen D: Multimodality image registration by maximization of quantitative-qualitative measure of mutual information. Pattern Recognition 2008,41(1):285-298. 10.1016/j.patcog.2007.04.002
Kadir T, Brady M: Saliency, scale and image description. International Journal of Computer Vision 2001,45(2):83-105. 10.1023/A:1012460413855
Itti L, Koch C, Niebur E: A model of saliency-based visual attention for rapid scene analysis. IEEE Transactions on Pattern Analysis and Machine Intelligence 1998,20(11):1254-1259. 10.1109/34.730558
Itti L, Koch C: A saliency-based search mechanism for overt and covert shifts of visual attention. Vision Research 2000,40(10–12):1489-1506.
Feng S, Xu D, Yang X: Attention-driven salient edge(s) and region(s) extraction with application to CBIR. Signal Processing 2010,90(1):1-15. 10.1016/j.sigpro.2009.05.017
Chen H-Y, Leou J-J: Saliency-directed image interpolation using particle swarm optimization. Signal Processing 2009,90(5):1676-1692.
Bergholm F: Edge focussing. IEEE Transactions on Pattern Analysis and Machine Intelligence 1987,9(6):726-741.
Deriche R, Giraudon G: A computational approach for corner and vertex detection. International Journal of Computer Vision 1993,10(2):101-124. 10.1007/BF01420733
Renninger LW, Verghese P, Coughlan J: Where to look next? Eye movements reduce local uncertainty. Journal of Vision 2007,7(3, article 6):1-17.
Greenspan H, Belongie S, Goodman R, Perona P, Rakshit S, Anderson CH: Overcomplete steerable pyramid filters and rotation invariance. Proceedings of the IEEE Computer Society Conference on Computer Vision and Pattern Recognition, June 1994, Seattle, Wash, USA 222-228.
Cannon MW, Fullenkamp SC: A model for inhibitory lateral interaction effects in perceived contrast. Vision Research 1996,36(8):1115-1125. 10.1016/0042-6989(95)00180-8
Belis M, Guiasu S: A quantitative-qualitative measure of information in cybernetic systems. IEEE Transactions on Information Theory 1968, 14: 593-594. 10.1109/TIT.1968.1054185
Cover TM, Thomas JA: Elements of Information Theory. Wiley, New York, NY, USA; 1991.
Jenkinson M, Smith S: A global optimisation method for robust affine registration of brain images. Medical Image Analysis 2001,5(2):143-156. 10.1016/S1361-8415(01)00036-6
Press WH, Flannery BP, Teukolsky SA, Vetterling WT: Numerical Recipes in C. 2nd edition. Cambridge University Press, Cambridge, UK; 1992.
Thévenaz P, Unser M: Optimization of mutual information for multiresolution image registration. IEEE Transactions on Image Processing 2000,9(12):2083-2099. 10.1109/83.887976
The Insight Segmentation and Registration Toolkit http://www.itk.org/
Studholme C, Hill DLG, Hawkes DJ: An overlap invariant entropy measure of 3D medical image alignment. Pattern Recognition 1999,32(1):71-86. 10.1016/S0031-3203(98)00091-0
Acknowledgments
The authors would like to thank Dr. Vivian S. Lee, Professor of Radiology, Physiology, and Neuroscience, Vice-Dean for Science, Senior Vice-President, and Chief Scientific Officer, New York University Medical Center, for providing the datasets. This work was supported by NUS Grant R-263-000-470-112.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Mahapatra, D., Sun, Y. Rigid Registration of Renal Perfusion Images Using a Neurobiology-Based Visual Saliency Model. J Image Video Proc 2010, 195640 (2010). https://doi.org/10.1155/2010/195640
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1155/2010/195640
 to eliminate modality or feature-dependent amplitude differences. We set
to eliminate modality or feature-dependent amplitude differences. We set  in our experiments.
in our experiments. , and calculate the average
, and calculate the average 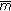 of its other local maxima.
of its other local maxima. .
. D
D indicates the original image;
indicates the original image;  indicates a subsampling factor of
indicates a subsampling factor of 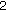 ,
,  indicates a factor of
indicates a factor of  , and
, and  indicates a subsampling factor of
indicates a subsampling factor of  .
. , we perform an exhaustive search individually for each DOF and the optimal parameters are used to transform the image. The search range is
, we perform an exhaustive search individually for each DOF and the optimal parameters are used to transform the image. The search range is  voxels for translation along
voxels for translation along  -,
-,  -,
-,  -axis (
-axis ( ) and
) and  degree for rotation about
degree for rotation about  -,
-, 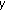 -,
-,  -axis (
-axis (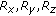 ).
).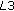 . The DOFs are individually optimized in two passes: first, rotation parameters over a search range of
. The DOFs are individually optimized in two passes: first, rotation parameters over a search range of 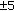 degrees and then
degrees and then 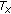 ,
, 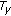 , and
, and  with search ranges of
with search ranges of  5,
5,  5, and
5, and  2 voxels. The optimal parameters are used to transform the volume and a second pass with the same sequence of steps is performed. The volume is transformed only if the parameters from the second pass indicate a better match than the parameters from first pass
2 voxels. The optimal parameters are used to transform the volume and a second pass with the same sequence of steps is performed. The volume is transformed only if the parameters from the second pass indicate a better match than the parameters from first pass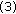 is repeated at a finer resolution level
is repeated at a finer resolution level 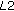 of the image.
of the image. are interpolated to
are interpolated to  and an exhaustive search is carried out for
and an exhaustive search is carried out for  (
( 3 degrees),
3 degrees), 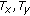 (
( 5 voxels) and
5 voxels) and  (
( 2 voxels).
2 voxels).






