- Research Article
- Open access
- Published:
Context-Based Defading of Archive Photographs
EURASIP Journal on Image and Video Processing volume 2009, Article number: 986183 (2009)
Abstract
We present an algorithm for the enhancement of contrast in digitized archive photographic prints. It aims at producing an adaptive enhancement based on the local context of each pixel and is able to operate without direct user's intervention. A relation between the variation of contrast at different resolutions and the local Lipschitz regularity of the image is exploited. In this way, each pixel is defaded according to its nature: noise, edge, or smooth region. This strategy provides for an algorithm that drastically reduces typical, annoying artifacts like halo effects and noise amplification.
1. Introduction
Antique photographic prints are very often subject to fading. Two typical examples of faded images are shown in Figure 1. Fading can be described using a model based on silver oxidation. The intensity and speed of this process are extremely variable and depend on the technology used to get the print as well as on the way the print under consideration was processed. Indeed, several factors influence the stability of a print. In the oldest salted papers, fading can be traced to the presence of sulphur. Its source may be intrinsic, due to hyposulphites left in the paper, or extrinsic, from the atmosphere [1]. A proper storage environment with controlled temperature and humidity is of course essential in order to preserve the quality of the original art. In particular, humidity is the prime factor to be considered for black and white prints. The lowest possible temperature that keeps the relative humidity (RH) under 30 percent should then be chosen [2]. However, in many cases the prints may have been placed in such an environment only recently, after the fading itself has manifested. Moreover, items exposed at exhibitions, or handled often, are particularly subject to degradations.
In order to enable the researcher or the public at large to visualize an image of the faded photograph as similar as possible to the original one, digital acquisition and processing is the only possible approach. Photographic archives acquire their images using professional scanning equipment and create digital versions of their art. The latter can then undergo a process of "virtual" restoration, for example, through a proper contrast enhancement algorithm.
Contrast enhancement is a well-known and challenging problem in image processing. In general, it aims at a recovery of the original vividness of images having a suboptimal contrast. A wide range of approaches have been proposed in literature in both the spatial and transform domains. Examples in the transform domain are alpha-rooting techniques, and techniques based on scaling the DCT coefficients. Alpha-rooting was first presented in [3], and it has been successively modified in [4–6], since it can be combined with different transforms. A recent version of alpha-rooting is described in [7]; it is based on properties of a tensor representation of the DFT. A DCT-domain operation is suggested in [8], where all the three attributes of brightness, contrast, and color of an image are addressed. It is based on a simple and computationally efficient algorithm, that only requires scaling of the DCT coefficients—mostly by a factor which remains constant in a block.
In the spatial domain, in addition to the use of simple linear techniques which emphasize the high-frequency contents of an image (the so-called unsharp masking approach), the most famous approaches are probably the Retinex model, based on Land's studies [9], and histogram equalization [10]. A set of modifications has been proposed for the improvement of these methods. In particular, it is interesting to note that both methods have evolved to include a multiscale (i.e., multiresolution) version, based on convolution with smoothing kernels. The evolution of the methods has incorporated the estimation of a context, based on a global measure in a suitable neighborhood, allowing adaptive enhancement [11–14]. In fact, there is a general agreement about the fact that these two factors greatly improve the performance of any contrast-enhancement framework [15]. However, they are also responsible for unavoidable undesired artifacts like oversmoothing (with a loss of details) or excessive enhancement (with a resulting amplification of noise and/or halo effects) [16]. Even though some sophisticated approaches have been proposed for their reduction [17, 18], these artifacts remain an aspect to be considered in the design of any contrast-enhancement framework. The situation is even more difficult when scanned antique photographic prints are processed. In this case, the presence of defects in the original art may introduce specific artifacts in the digital item, which in turn produce particularly annoying effects if conventional enhancement techniques are applied.
In this paper we present an adaptive enhancement tool that tries to overcome the above-mentioned problems. It is based on a multiscale approach that exploits the local context. In particular, it exploits the link between the change of contrast (as the resolution is increased) and the local Lipschitz regularity of the image [19, 20]. Such a link can be used for asserting the (possibly) noisy nature of each pixel, avoiding convolutions with kernels that would introduce the aforementioned artifacts. On the other hand, a measure of contrast at different resolutions allows to exploit visibility laws, such as the Weber-Fechner law; they are used in the assessment of the importance, and then the enhancement of each pixel of the image under study.
After the pixels have been classified (edge, noise, or smooth region), their contrast is changed appropriately. Then, at a successive stage, an optimal (global) gamma correction tool that exploits the results in [21] is performed. The proposed framework has been tested on various digitized historical photographic prints subjected to fading. Experimental results show good results in terms of subjective quality and a good efficiency even in critical cases. To make a more objective evaluation of the results, comparisons with representative contrast enhancement methods have been introduced. Moreover, several quality measures have been used to quantify the visual appearance of the restored images.
The paper is organized as follows. Section 2 presents the proposed model; it includes the detailed algorithm and a description of each of its three phases. Section 3 contains some experimental results and comparative studies. Finally, some discussions, conclusions, and guidelines for future research are the topic of Section 4.
2. The Proposed Model
The proposed method, initially explored in [22], consists of three main stages. In the first one, the image is preprocessed and its pixels are classified according to the inferred type of damage suffered. In particular, we check if a pixel belongs to a blotch (a common fault in antique photos) in the image. This operation allows for a more appropriate estimation of the parameters in the two remaining stages. In the second stage, the link between the local Lipschitz regularity and the change of contrast of the image across scales is exploited; after this stage, adaptive contrast enhancement can be performed on the faded image. The aim of the second stage is to differentiate the type of defading to be applied to each pixel according to its nature (edge, noise, or flat region). In the third stage, the image is defaded using a contrast-enhancement tool that is based on the classical characteristic curve  , with
, with  (as in gamma correction). In order to automatically estimate an optimal value of
(as in gamma correction). In order to automatically estimate an optimal value of  , we exploit the results presented in [21] that are based on the following observation: visually pleasant images show a sort of orthogonality between the local first moment and the local second central moment of the distribution of the luminance values. It is interesting to note that [23] reports a statistical independence between luminance and contrast in natural images. (Mante et al. use the weighted sums
, we exploit the results presented in [21] that are based on the following observation: visually pleasant images show a sort of orthogonality between the local first moment and the local second central moment of the distribution of the luminance values. It is interesting to note that [23] reports a statistical independence between luminance and contrast in natural images. (Mante et al. use the weighted sums  and
and  to measure local contrast and luminance, resp., where
to measure local contrast and luminance, resp., where  is the pixelwise luminance, and the weights
is the pixelwise luminance, and the weights  decrease with the distance from the center of the context.) In the following, the aforementioned stages are described in detail.
decrease with the distance from the center of the context.) In the following, the aforementioned stages are described in detail.
2.1. Deblotching
In the first stage, roughly called deblotching, the regions with a color that is stronger than the more common (faded) colors in the remaining parts of the image are detected. We use the term "strong" here since, for achromatic images, to say that a region is saturated black or white is perhaps misleading. Observing such dark and bright blotches in Figure 1, it can be seen that there are two main reasons for performing deblotching. First, blotches would increase their appearance after any contrast enhancement operation with the result that the defaded image would be conspicuously spotted, compromising its global visual quality. The second reason is that blotch pixels have statistical properties that are different from those in the rest of the image. Hence, to ignore blotch pixels allows an improved estimation of the parameters in the remaining stages.
The detection of blotches is usually difficult because of their variability in shape and intensity. However, it is a bit easier in the case of faded images because blotches are more evident in a faded context. It is then better to detect blotches using the (local) contrast rather than the plain pixel intensity. In fact, the blotches have a stressed appearance in the contrast domain, as shown in Figure 2. We define the scale-dependent contrast  as follows:
as follows:

where  is our faded image,
is our faded image,  is the mean of the intensity
is the mean of the intensity  in a region
in a region  centered in
centered in  and
and  is a scale (or resolution) parameter. With this definition, which pretty much agrees with Weber's law, blotches become outliers and can be easily detected by straightforward thresholding applied on
is a scale (or resolution) parameter. With this definition, which pretty much agrees with Weber's law, blotches become outliers and can be easily detected by straightforward thresholding applied on  . The threshold
. The threshold  can be either tuned manually or set at
can be either tuned manually or set at  , where
, where  is the standard deviation of
is the standard deviation of  . The latter choice is robust under the hypothesis that blotches are evident on this kind of images, as shown in Figure 1. Even though the detection method we propose may seem blunt, it is perfectly acceptable in the context in which it is used. In other words, it is mainly a preprocessing tool which makes the successive computation of the Lipschitz factor more correct—see Figure 3. It is worth noticing that the contrast
. The latter choice is robust under the hypothesis that blotches are evident on this kind of images, as shown in Figure 1. Even though the detection method we propose may seem blunt, it is perfectly acceptable in the context in which it is used. In other words, it is mainly a preprocessing tool which makes the successive computation of the Lipschitz factor more correct—see Figure 3. It is worth noticing that the contrast  in (1) is considered with its sign. This enable us to distinguish between pixels that are darker or brighter than their background and then to apply a proper enhancement.
in (1) is considered with its sign. This enable us to distinguish between pixels that are darker or brighter than their background and then to apply a proper enhancement.
2.2. Lipschitz-Based Contrast Enhancement
The phenomenon of fading is often accompanied by noise resulting from a chemical degradation of the photographic emulsion. The aim of this stage is then to produce an image where the contrast of each pixel is changed depending on whether it is part of a noisy, an edge, or a flat region. The analysis carried out in this section is local; global corrections are addressed in the third phase. We are interested here in analyzing the link between the pointwise Lipschitz regularity and the variation of contrast of the image. It is well-known that the Lipschitz coefficient gives information about the (possibly) noisy nature as well as the regularity of each point [19].
In particular, bearing in mind the definition given in (1), we compute the variation of contrast with scale (i.e., changing the resolution) at a generic pixel  as
as

We assume that in a neighborhood of the pixel  the image
the image  is locally smooth. This means that it can be locally approximated by a polynomial
is locally smooth. This means that it can be locally approximated by a polynomial  of degree
of degree  in the variable
in the variable  . It turns out that the local background of the pixel at
. It turns out that the local background of the pixel at  is still a polynomial function. In fact, it is the mean value of
is still a polynomial function. In fact, it is the mean value of  in the region
in the region  . More precisely,
. More precisely,

where the integral is a polynomial function whose degree does not exceed  , as proved in the appendix. It turns out that
, as proved in the appendix. It turns out that  is a polynomial function
is a polynomial function  with respect to
with respect to  where
where  while
while  Hence
Hence  (
( means that
means that  has the same order of
has the same order of  ).
).
As a result, the contrast variation can be linked to the Lipschitz regularity as

Integrating by separation of variables,

we get  , where
, where  indicates the linear dependence, so that
indicates the linear dependence, so that

It is important to notice that the result above permits to impose some constraints on choices usually made by hand in other methods proposed in literature. First of all, only two scale levels are required for the discrimination between noisy and uncorrupted points of the faded image. Indeed, taking into account the pointwise nature of the noise, two levels among all the possible ones can be selected. Furthermore, no additional thresholding is required for discriminating the nature of each pixel and selecting the corresponding enhancement function. Finally, the size of the context  used for the computation of the contrast coincides with the support of the regularizing function, and the mean can be seen as the convolution between the image and a Haar basis function at a given scale. It is obvious that the aforementioned considerations are valid just in case of contrast enhancement under noise and not in general. In the latter case, the parameters above have to take into account the local frequency information of the image as well; consider, for example, textures. This would imply the use of a more sophisticated measure of contrast that would take into account not only the spatial information (local mean) but also the frequency (in terms of dominant frequency values) in the same region.
used for the computation of the contrast coincides with the support of the regularizing function, and the mean can be seen as the convolution between the image and a Haar basis function at a given scale. It is obvious that the aforementioned considerations are valid just in case of contrast enhancement under noise and not in general. In the latter case, the parameters above have to take into account the local frequency information of the image as well; consider, for example, textures. This would imply the use of a more sophisticated measure of contrast that would take into account not only the spatial information (local mean) but also the frequency (in terms of dominant frequency values) in the same region.
Coming back to (6), the value of  can be used in a power-law correction. In fact, considering the contrast enhancement map
can be used in a power-law correction. In fact, considering the contrast enhancement map  , we have the effects shown in Figure 4: a lower enhancement for noisy pixels (
, we have the effects shown in Figure 4: a lower enhancement for noisy pixels ( ) than for uncorrupted points (
) than for uncorrupted points ( ). Moreover, where the regularity is higher (larger
). Moreover, where the regularity is higher (larger  s), a stronger enhancement is performed. In other words, the contrast of flat regions is increased, giving the image the vividness characteristic of natural images [24]. On the contrary, edges (characterized by smaller but still positive
s), a stronger enhancement is performed. In other words, the contrast of flat regions is increased, giving the image the vividness characteristic of natural images [24]. On the contrary, edges (characterized by smaller but still positive  s) are slightly less enhanced, avoiding the halo effect which is common to many contrast enhancement approaches. It is worth highlighting that the aforementioned effects are based on the hypothesis that the gray levels of a faded image are located in the highest portion of the intensity range.
s) are slightly less enhanced, avoiding the halo effect which is common to many contrast enhancement approaches. It is worth highlighting that the aforementioned effects are based on the hypothesis that the gray levels of a faded image are located in the highest portion of the intensity range.
Summing up, this phase permits to obtain an image that, even if still faded, has been changed in a space-varying way in agreement with its local regularity. As a result, its noisy pixels are less emphasized while the contrast of uncorrupted points is increased accounting for their context, as it is shown in Figure 5.
2.3. Defading and Image-Quality Measure
To complete the defading process, a global (i.e., uniform in the image) luminance mapping is applied. It is based again on a power-law function,  . This mapping depends on the choice of the parameter
. This mapping depends on the choice of the parameter  which is made using an image quality measure. The distribution of the local standard deviation
which is made using an image quality measure. The distribution of the local standard deviation  with respect to the local average
with respect to the local average  of the luminance has been recently used in order to define a figure of merit that was used in a restoration algorithm applied to faded images [21]. It has been shown that these two statistical parameters live constrained in a bell-shaped region of the plane (
of the luminance has been recently used in order to define a figure of merit that was used in a restoration algorithm applied to faded images [21]. It has been shown that these two statistical parameters live constrained in a bell-shaped region of the plane ( ,
,  ) [25]. We use here the same approach, in order to get an estimate of the optimal values of the parameters used in the algorithm described above.
) [25]. We use here the same approach, in order to get an estimate of the optimal values of the parameters used in the algorithm described above.
Let us suppose that we acquire a digital image from a given real-world scene using an ideal linear device and consider only its luminance values for simplicity. We subdivide the image into  adjacent blocks, and calculate the standard deviation
adjacent blocks, and calculate the standard deviation  and the average
and the average  of the luminance or gray level within each block. In the (
of the luminance or gray level within each block. In the ( ,
,  ) plane each block is then represented by a point. If we imagine to repeat this procedure for a huge set of scenes with all sorts of conceivable contents, and to display the corresponding values (
) plane each block is then represented by a point. If we imagine to repeat this procedure for a huge set of scenes with all sorts of conceivable contents, and to display the corresponding values ( ,
,  ) in a single plane, we will probably get a cloud of points showing no correlation between
) in a single plane, we will probably get a cloud of points showing no correlation between  and
and  . There is no reason indeed why the average of the luminance of an object in the real world should influence the standard deviation of the same luminance. Notice that this consideration does not contradict Weber's law, which is related to our perception of the scene, and is not a property of the scene itself. The situation is different if, as it happens in practice, the dynamic range of the acquisition device is limited; in this case, very dark and very bright blocks present a limited deviation. In fact, it can be demonstrated that the values of
. There is no reason indeed why the average of the luminance of an object in the real world should influence the standard deviation of the same luminance. Notice that this consideration does not contradict Weber's law, which is related to our perception of the scene, and is not a property of the scene itself. The situation is different if, as it happens in practice, the dynamic range of the acquisition device is limited; in this case, very dark and very bright blocks present a limited deviation. In fact, it can be demonstrated that the values of  lie now in a limited range bounded above by a bell-shaped function of the average; the function takes its maximum value when the average is half the available range and falls to zero when the average corresponds to the minimum or the maximum of the luminance range [25].
lie now in a limited range bounded above by a bell-shaped function of the average; the function takes its maximum value when the average is half the available range and falls to zero when the average corresponds to the minimum or the maximum of the luminance range [25].
A proper distribution of the points in the ( ,
,  ) plane, and more precisely in the well-defined region mentioned above, can be taken as an indicator of image quality (see also [26].) However, no particular distribution can be used as a requirement for image quality in general because good-looking images exist with all sorts of distributions; thus, more indicators are needed. However, it makes sense to speak of a proper distribution in the case of restored images of faded photographic prints. This category of images indeed shows a degradation which brings the luminance averages near the higher portion of the range of
) plane, and more precisely in the well-defined region mentioned above, can be taken as an indicator of image quality (see also [26].) However, no particular distribution can be used as a requirement for image quality in general because good-looking images exist with all sorts of distributions; thus, more indicators are needed. However, it makes sense to speak of a proper distribution in the case of restored images of faded photographic prints. This category of images indeed shows a degradation which brings the luminance averages near the higher portion of the range of  and, hence, the corresponding values of
and, hence, the corresponding values of  are constrained to be relatively small. The effectiveness of the enhancement process of the digitally acquired version of the print can thus be evaluated based on the obtained increment in the value of
are constrained to be relatively small. The effectiveness of the enhancement process of the digitally acquired version of the print can thus be evaluated based on the obtained increment in the value of  . More specifically, the correlation coefficient between
. More specifically, the correlation coefficient between  and
and  , which can be estimated via
, which can be estimated via

tends to assume negative values for the degraded picture. After the processing, the shape of the cloud of points in the ( ,
,  ) plane corresponds to values of
) plane corresponds to values of  close or equal to zero. Thus, we use closeness of
close or equal to zero. Thus, we use closeness of  to 0 as a quality criterion for the choice of the parameter in Phase 3, as it will be shown in the following section and in Figure 6.
to 0 as a quality criterion for the choice of the parameter in Phase 3, as it will be shown in the following section and in Figure 6.
It is worth outlining that image quality measurement is of course a complex subject. The total amount of contrast in an image is sometimes considered as a measure of image quality since, quite often, the larger the total contrast, the better the image. In fact, for the restoration of faded prints, gamma correction increases the average value of  . In addition to our Weber-related definition of contrast, and that in [23], one further definition is the well-known Michelson contrast [28]:
. In addition to our Weber-related definition of contrast, and that in [23], one further definition is the well-known Michelson contrast [28]:

where  and
and  are the maximum and the minimum of the intensities in the context. For the measurement of contrast, the use of the plain local range (i.e.,
are the maximum and the minimum of the intensities in the context. For the measurement of contrast, the use of the plain local range (i.e.,  ) [26] or the range of the logarithm of intensities is also interesting. Both the standard deviation (also called rms contrast [28]) and the range are measures of statistical dispersion. Other quality measures are based on LIP arithmetic [29]. Its use allowed Agaian et al. [5, 30] to propose a set of quality parameters that measure total contrast; they are based on LIP and LIP-entropy versions of Michelson (local) contrast. After adding local contrast (again, using LIP arithmetic), the quality measures AME1 and AME2 can be written:
) [26] or the range of the logarithm of intensities is also interesting. Both the standard deviation (also called rms contrast [28]) and the range are measures of statistical dispersion. Other quality measures are based on LIP arithmetic [29]. Its use allowed Agaian et al. [5, 30] to propose a set of quality parameters that measure total contrast; they are based on LIP and LIP-entropy versions of Michelson (local) contrast. After adding local contrast (again, using LIP arithmetic), the quality measures AME1 and AME2 can be written:

In LIP arithmetic (assuming the bounded range [ ] for the intensity magnitude) one has, for f and g intensity values and
] for the intensity magnitude) one has, for f and g intensity values and  a real scalar,
a real scalar,  ;
;  ;
;  , and
, and  . LIP arithmetic has the important advantage of respecting the bounded luminance range, for example, [
. LIP arithmetic has the important advantage of respecting the bounded luminance range, for example, [ ], of an image; also, Weber's law can be expressed in LIP arithmetic. Thus, LIP arithmetic is advisable when the result of the operation is to be used as an intensity value, and perhaps also in the present case since LIP arithmetic is related to human visual perception issues. The entropy version AME2 stresses the importance of uniformly distributed local contrast. The mentioned quality indicators will be considered in the experiments described in Section 3.
], of an image; also, Weber's law can be expressed in LIP arithmetic. Thus, LIP arithmetic is advisable when the result of the operation is to be used as an intensity value, and perhaps also in the present case since LIP arithmetic is related to human visual perception issues. The entropy version AME2 stresses the importance of uniformly distributed local contrast. The mentioned quality indicators will be considered in the experiments described in Section 3.
2.4. The Algorithm
Phase 
-
(i)
For each pixel
 , compute the contrast matrix
, compute the contrast matrix 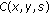 at a given scale
at a given scale  , as in (1).
, as in (1). -
(ii)
Compute the standard deviation
 of
of 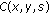 .
. -
(iii)
Hard threshold
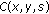 using as threshold value
using as threshold value 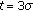 . Let
. Let  .
.
Phase 
-
(i)
Compute
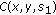 at another scale level
at another scale level  .
. -
(ii)
Estimate
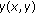 using (6) if
using (6) if 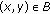 , else
, else 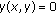 .
. -
(iii)
Pointwise
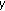 correct
correct  through the function
through the function 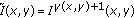 .
.
Phase 
Let  and
and  , respectively, be the minimum and maximum value of
, respectively, be the minimum and maximum value of  , where the points in
, where the points in  have been neglected. For each
have been neglected. For each  ,
,
(i)stretch  as follows:
as follows:  ;
;
(ii)compute  using (7) and select
using (7) and select  .
.
Then, stretch  using the optimal
using the optimal  .
.
It is worth stressing that sepia images are the input of the proposed algorithm. For this reason, only their luminance component has been processed and is shown; the two chrominance components can be kept unchanged if desired.
3. Experimental Results
The proposed framework has been tested on various images coming from the Fratelli Alinari Archive in Florence, Italy. In this paper we consider the two images shown in Figure 1 and the ones on the left side of Figure 8.
All the images show evident opaque blotches. Using blocks  of size
of size  pixels as the context for computing the local contrast in 1, the maps of blotches achieved in the first phase are quite satisfactory: almost all the blotches are detected, as shown in Figure 3. In the second phase, the estimate of the pointwise
pixels as the context for computing the local contrast in 1, the maps of blotches achieved in the first phase are quite satisfactory: almost all the blotches are detected, as shown in Figure 3. In the second phase, the estimate of the pointwise  requires the computation of the contrast at two different resolutions. Along with the size
requires the computation of the contrast at two different resolutions. Along with the size  already used in the first stage, a square window of size
already used in the first stage, a square window of size  is used here. It is worth emphasizing that very similar values of the corresponding
is used here. It is worth emphasizing that very similar values of the corresponding  are obtained for different choices of the window size. This is encouraging since the estimate of the pointwise
are obtained for different choices of the window size. This is encouraging since the estimate of the pointwise  in (6) does not consider the constants. Performing the correction through the characteristic curve
in (6) does not consider the constants. Performing the correction through the characteristic curve  we achieve the result in Figure 5. It can be noted that the resulting images are still faded but with a drastic reduction of the relative noise contribution. The output coming from the second phase is finally enhanced via a
we achieve the result in Figure 5. It can be noted that the resulting images are still faded but with a drastic reduction of the relative noise contribution. The output coming from the second phase is finally enhanced via a  curve in the third phase.
curve in the third phase.  is a global parameter (one for all image pixels) and in our experiments it assumed the following values
is a global parameter (one for all image pixels) and in our experiments it assumed the following values  ,
,  ,
,  ,
,  and
and  respectively, for the Horse rider, Arena di Pola, View, Woman Face, and full size Horse Rider images. They have been selected in correspondence to
respectively, for the Horse rider, Arena di Pola, View, Woman Face, and full size Horse Rider images. They have been selected in correspondence to  since a good matching exists with the perceived image quality. Figure 6 shows the
since a good matching exists with the perceived image quality. Figure 6 shows the  values obtained as a function of
values obtained as a function of  for the two test images Horse Rider (left) and Arena di Pola (right). They exhibit a smooth and monotonic behaviour; the optimal values of
for the two test images Horse Rider (left) and Arena di Pola (right). They exhibit a smooth and monotonic behaviour; the optimal values of  are indicated as those for which
are indicated as those for which  . The final results for the adopted images are shown in Figures 7 and 8 (right).
. The final results for the adopted images are shown in Figures 7 and 8 (right).
Top to bottom, left to right: faded Horse Rider image; EME, EME with entropy, EME using the Michelson contrast, and AME quality measures, as defined in [5]; second derivative of AME with respect to  ; values obtained as a function of α; defaded Horse Rider image obtained using the optimal α value. It is worth noticing that the AME measure has an interesting point in correspondence to the main change of curvature (minimum of its second derivative with respect to α), which coincides with the optimal α value selected by the
; values obtained as a function of α; defaded Horse Rider image obtained using the optimal α value. It is worth noticing that the AME measure has an interesting point in correspondence to the main change of curvature (minimum of its second derivative with respect to α), which coincides with the optimal α value selected by the  scheme.
scheme.
To test the visual quality of the results, we use four of the quality measures proposed in [5], as alternative measures to the  distribution. They, respectively, are
distribution. They, respectively, are  ,
,  with entropy,
with entropy,  using the contrast of Michelson, and
using the contrast of Michelson, and  , and they have been evaluated in the third phase of the algorithm for each value of
, and they have been evaluated in the third phase of the algorithm for each value of  (global enhancement parameter). As depicted in Figure 9, they increase with
(global enhancement parameter). As depicted in Figure 9, they increase with  —see also Table 1. The problem is now to define some critical points in these curves that could be related to the quality of the image. To this aim, for simplicity we analyse the
—see also Table 1. The problem is now to define some critical points in these curves that could be related to the quality of the image. To this aim, for simplicity we analyse the  measure that, as we saw in Section 2.3, is an entropy-based measure related to the Michelson contrast. An interesting aspect concerns its curvature. In fact, its second derivative shows a minimum (a "good point") that corresponds to a main change of curvature. It is interesting to note that it occurs also in correspondence to the optimal value of
measure that, as we saw in Section 2.3, is an entropy-based measure related to the Michelson contrast. An interesting aspect concerns its curvature. In fact, its second derivative shows a minimum (a "good point") that corresponds to a main change of curvature. It is interesting to note that it occurs also in correspondence to the optimal value of  , as selected with the
, as selected with the  scheme (see Figure 9).
scheme (see Figure 9).
 values and quality metrics of the corresponding
values and quality metrics of the corresponding  corrected image, as depicted in Figure 9.
corrected image, as depicted in Figure 9.It is important to stress that all the involved parameters in the proposed model are automatically tuned. In particular, this is true for the adaptive enhancement based on Lipschitz regularity and for the estimation of the global enhancement factor. In fact, the main property of the latter approach as a quality measure is the fact that the good point is univocally determined for each image. On the contrary, conventional multiscale methods often require to tune more than one threshold—depending on the adopted nonlinear contrast-enhancement function, the allowed level of noise, and the employed quality measure. Figure 10 shows the enhanced images obtained using the wavelet-based method in [27] (left), a simple linear contrast stretching (right), and the  -rooting method in [5]. Neither is satisfactory: in the first case, noise is still visible, in the second one highly detailed regions are excessively smoothed, and in the third one the image is grayish with emphasized bright details. On the contrary, as Figure 11 shows, the defaded image using the proposed approach has vivid colors, well enhanced edges, and no oversmoothed regions.
-rooting method in [5]. Neither is satisfactory: in the first case, noise is still visible, in the second one highly detailed regions are excessively smoothed, and in the third one the image is grayish with emphasized bright details. On the contrary, as Figure 11 shows, the defaded image using the proposed approach has vivid colors, well enhanced edges, and no oversmoothed regions.
Left : Zoom of Horse rider, defaded with the proposed scheme. No halo effects appear, and there is neither oversmoothing nor excessive noise enhancement. Right: Zoom of Horse rider, defaded with the adaptive multiresolution method in [27] (top), and with linear contrast stretching (bottom).
The restoration application we address is not characterized by real-time needs; nonetheless, the operations performed by the proposed algorithm are very simple and the required computing time is comparable to the ones required by the mentioned competing approaches.
4. Discussion and Conclusions
In this paper we have presented a framework aimed at giving faded images their original vividness. After the application of an adaptive technique of contrast enhancement that exploits the link between local Lipschitz image regularity and the change of contrast, a global power-law correction is performed. The proposed model allows for a gradual enhancement of the image that avoids drawbacks like halo and noise amplification. In a forthcoming paper we explore further the theoretical framework presented in Section 2.2, using more sophisticated bases such as those in [31]. For the specific usage on faded photographic prints, the experiments we have performed indicate that the proposed method gives a satisfactory performance. However, a few issues should be addressed in future works. First of all we observe that the estimate we use for the Lipschitz regularity is slightly noisy; this affects in particular quasihomogeneous areas where the contrast is very low. An improved definition of contrast that permits a stronger dependence of the power-term correction on the local characteristics of smooth image areas should be devised. Finally, it would be convenient if an optimum balance between the local and the global correction stages could be automatically attained, since the ( ,
,  ) method does not yield a satisfactory input for this purpose. For pictures having a nonuniform exposure to light, it would be more reasonable to differently treat two or more portions of the image itself. In this case, some user intervention would be required.
) method does not yield a satisfactory input for this purpose. For pictures having a nonuniform exposure to light, it would be more reasonable to differently treat two or more portions of the image itself. In this case, some user intervention would be required.
References
Reilly JM: The question of permanence. In The Albumen & Salted Paper Book: The History and Practice of Photographic Printing, 1840–1895. Light Impressions, Rochester, NY, USA; 1980.
Wilhelm H, Brower C: The Permanence and Care of Color Photographs. Preservation, Grinnell, Iowa, USA; 1993.
Jain AK: Fundamentals of Digital Image Processing. Prentice-Hall, Upper Saddle River, NJ, USA; 1989.
Aghagolzadeh S, Ersoy OK: Transform image enhancement. Optical Engineering 1992,31(3):614-626. 10.1117/12.56095
Agaian SS, Silver B, Panetta KA: Transform coefficient histogram-based image enhancement algorithms using contrast entropy. IEEE Transactions on Image Processing 2007,16(3):741-758.
Panetta KA, Wharton EJ, Agaian SS: Human visual system-based image enhancement and logarithmic contrast measure. IEEE Transactions on Systems, Man, and Cybernetics, Part B 2008,38(1):174-188.
Turkay Arslan F, Grigoryan AM: Fast splitting alpha-rooting method of image enhancement: tensor representation. IEEE Transactions on Image Processing 2006,15(11):3375-3384.
Mukherjee J, Mitra SK: Enhancement of color images by scaling the DCT coefficients. IEEE Transactions on Image Processing 2008,17(10):1783-1794.
Land EH, McCann JJ: Lightness and retinex theory. Journal of the Optical Society of America 1971,61(1):1-11. 10.1364/JOSA.61.000001
Hummel R: Image enhancement by histogram transformation. Comput Graphics Image Process 1977,6(2):184-195. 10.1016/S0146-664X(77)80011-7
Jobson DJ, Rahman Z-U, Woodell GA: A multiscale retinex for bridging the gap between color images and the human observation of scenes. IEEE Transactions on Image Processing 1997,6(7):965-976. 10.1109/83.597272
Tao L, Asari VK: Modified luminance based MSRCR for fast and efficient image enhancement. Proceedings of the 32nd IEEE Applied Imagery Pattern Recognition Workshop (AIPR '03), 2003, Washington, DC, USA 174-179.
Pizer SM, Zimmerman JB, Staab EV: Adaptive grey level assignment in CT scan display. Journal of Computer Assisted Tomography 1984,8(2):300-305.
Jin Y, Fayad LM, Laine AF: Contrast enhancement by multiscale adaptive histogram equalization. Wavelets: Applications in Signal and Image Processing IX, 2001, Proceedings of SPIE 206-213.
Yoon B-W, Song W-J: Image contrast enhancement based on the generalized histogram. Journal of Electronic Imaging 2007.,16(3):
Tao L, Asari VK: Adaptive and integrated neighborhood-dependent approach for nonlinear enhancement of color images. Journal of Electronic Imaging 2005.,14(4):
Pattanaik SN, Ferwerda JA, Fairchild MD, Greenberg DP: A multiscale model of adaptation and spatial vision for realistic image display. Proceedings of the Annual Conference on Computer Graphics (SIGGRAPH '98), July 1998, Orlando, Fla, USA 287-298.
Tumblin J, Turk G: LCIS: a boundary hierarchy for detail-preserving contrast reduction. Proceedings of the 26th Annual Conference on Computer Graphics and Interactive Techniques (SIGGRAPH '99), 1999 83-90.
Mallat S: A Wavelet Tour of Signal Processing. Academic Press, San Diego, Calif, USA; 1998.
Mallat S, Hwang WL: Singularity detection and processing with wavelets. IEEE Transactions on Information Theory 1992,38(2):617-643. 10.1109/18.119727
Ramponi G: Adaptive contrast improvement for still images and video frames. Proceedings of the IEEE-EURASIP Workshop on Nonlinear Signal and Image Processing (NSIP '07), September 2007, Bucharest, Romania
Bruni V, Ramponi G, Restrepo A, Vitulano D: Restoration of faded images without noise amplification. Proceedings of the 16th IEEE-EURASIP European Signal Processing Conference (EUSIPCO '08), 2008 SS6.2.4.1-SS6.2.4.5.
Mante V, Frazor RA, Bonin V, Geisler WS, Carandini M: Independence of luminance and contrast in natural scenes and in the early visual system. Nature Neuroscience 2005,8(12):1690-1697. 10.1038/nn1556
Gutierrez J, Ferri FJ, Malo J: Regularization operators for natural images based on nonlinear perception models. IEEE Transactions on Image Processing 2006,15(1):189-200.
Restrepo A, Ramponi G: Filtering and luminance correction for aged photographs. Image Processing: Algorithms and Systems VI, January 2008, San Jose, Calif, USA, Proceedings of SPIE 6812: 26-31.
Restrepo A, Ramponi G: Word descriptors of image quality based on local dispersion-versus-location distributions. Proceedings of the 16th European Signal Processing Conference (EUSIPCO '08), August 2008, Lausanne, Switzerland
Velde KV: Multi-scale color image enhancement. Proceedings of the IEEE International Conference on Image Processing (ICIP '99), October 1999, Kobe, Japan 3: 584-587.
Peli E: Contrast in complex images. Journal of the Optical Society of America A 1990,7(10):2032-2040. 10.1364/JOSAA.7.002032
Pinoli J-C, Debayle J: Logarithmic adaptive neighborhood image processing (LANIP): introduction, connections to human brightness perception, and application issues. EURASIP Journal on Advances in Signal Processing 2007, 2007:-22.
Agaian SS, Lentz KP, Grigoryan AM: A new measure of image enhancement. Proceedings of the of IASTED International Conference on Signal Processing and Communications, 2000
Gobbers JF, Vandergheynst P: Directional wavelet frames: design and algorithms. IEEE Transactions on Image Processing 2002, 11: 363-372. 10.1109/TIP.2002.999670
Acknowledgments
This work has been supported by the Italian Ministry of Education as a part of the Firb Project no. RBNE039LLC. The authors wish to thank F. lli Alinari SpA for providing the pictures used in the experiments.
Author information
Authors and Affiliations
Corresponding author
Appendix
The aim of this appendix is to show that the local background  , defined in (3), of a polynomial image
, defined in (3), of a polynomial image  of degree
of degree  is still a polynomial function
is still a polynomial function  of degree
of degree  , with
, with  .
.
Let  and
and  be two real numbers such that
be two real numbers such that  and let us consider the monomial with the highest degree of
and let us consider the monomial with the highest degree of  , that is,
, that is,  . Its contribution in
. Its contribution in  is
is


The numerator is a polynomial function with respect to  . If
. If  is its degree, then the function is a polynomial of degree
is its degree, then the function is a polynomial of degree  . Moreover,
. Moreover,


It turns out that the local background  is a polynomial function whose degree does not exceed
is a polynomial function whose degree does not exceed  .
.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License ( https://creativecommons.org/licenses/by/2.0 ), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Bruni (EURASIP Member), V., Ramponi, G., Restrepo, A. et al. Context-Based Defading of Archive Photographs. J Image Video Proc 2009, 986183 (2009). https://doi.org/10.1155/2009/986183
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2009/986183




 correction in the 2nd phase:
correction in the 2nd phase:  dotted,
dotted,  solid, and
solid, and  dashed.
dashed.


 values obtained as a function of
values obtained as a function of  and corresponding average values of the output image for Horse Rider (a) and Arena di Pola (b).
and corresponding average values of the output image for Horse Rider (a) and Arena di Pola (b).
 , compute the contrast matrix
, compute the contrast matrix 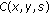 at a given scale
at a given scale  , as in (1).
, as in (1). of
of 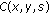 .
.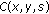 using as threshold value
using as threshold value 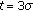 . Let
. Let  .
.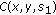 at another scale level
at another scale level  .
.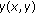 using (6) if
using (6) if 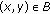 , else
, else 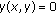 .
. correct
correct  through the function
through the function 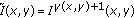 .
.



