- Research Article
- Open access
- Published:
Dynamic Quality Control for Transform Domain Wyner-Ziv Video Coding
EURASIP Journal on Image and Video Processing volume 2009, Article number: 978581 (2009)
Abstract
Wyner-Ziv is an emerging video coding paradigm based on the Slepian-Wolf and Wyner-Ziv theorems where video coding may be performed by exploiting the temporal correlation at the decoder and not anymore at the encoder as in conventional video coding. This approach should allow designing low-complexity encoders, targeting important emerging applications such as wireless surveillance and visual sensor networks, without any cost in terms of RD performance. However, the currently available WZ video codecs do not allow controlling the target quality in an efficient way which is a major limitation for some applications. In this context, the main objective of this paper is to propose an efficient quality control algorithm to maintain a uniform quality along time in low-encoding complexity WZ video coding by dynamically adapting the quantization parameters depending on the desired target quality without any a priori knowledge about the sequence characteristics. This objective will be reached in the context of the so-called Stanford WZ video codec architecture which is currently the most used in the literature.
1. Introduction
With the wide deployment of mobile and wireless networks, there are a growing number of applications requiring light video encoding complexity and robustness to packet losses while still reaching the highest possible compression efficiency. In several of these emerging applications, many senders simultaneously deliver data, notably video data, to a central receiver asking for a codec complexity budget paradigm opposite to the one used until now, where typically one sender serves many receivers, like in TV environments. While the decoding complexity was before a critical requirement, encoding complexity is now an essential factor for these emerging applications. To address these rising needs, some research groups revisited the video coding problem the light of some information theory results from the 70s: the Slepian-Wolf [1] and the Wyner-Ziv theorems [2]. According to the Slepian-Wolf theorem, the minimum rate needed to independently encode two statistically dependent discrete random sequences,  and
and  , is the same as for joint encoding this means for the encoding of
, is the same as for joint encoding this means for the encoding of  and
and  exploiting their mutual knowledge; this coding paradigm is known as distributed source coding (DSC). While the Slepian-Wolf theorem deals with lossless coding (with a vanishing error probability), Wyner and Ziv studied the case of lossy coding with side information (SI) at the decoder. The Wyner-Ziv (WZ) theorem [2] states that when the SI (i.e., the correlated source
exploiting their mutual knowledge; this coding paradigm is known as distributed source coding (DSC). While the Slepian-Wolf theorem deals with lossless coding (with a vanishing error probability), Wyner and Ziv studied the case of lossy coding with side information (SI) at the decoder. The Wyner-Ziv (WZ) theorem [2] states that when the SI (i.e., the correlated source  ) is made available only at the decoder, there is no coding efficiency loss in encoding
) is made available only at the decoder, there is no coding efficiency loss in encoding  , with respect to the case when joint encoding of
, with respect to the case when joint encoding of  and
and  is performed, if
is performed, if  and
and  are jointly Gaussian sequences and a mean-squared error distortion measure is used. This is a significant advantage for a large range of emerging application scenarios [3], such as those mentioned above, including wireless video cameras, wireless low-power surveillance, video conferencing with mobile devices, and visual sensor networks, since significant changes in the coding architectures are possible.
are jointly Gaussian sequences and a mean-squared error distortion measure is used. This is a significant advantage for a large range of emerging application scenarios [3], such as those mentioned above, including wireless video cameras, wireless low-power surveillance, video conferencing with mobile devices, and visual sensor networks, since significant changes in the coding architectures are possible.
With the "theoretical doors" opened by these theorems, the practical design of WZ video codecs, a particular case of DSC also known as distributed video coding (DVC), started around 2002, following important developments in channel coding technology. One of the first practical WZ video coding solutions has been developed at Stanford University [4]; this solution has become the most popular WZ video codec design in literature. The basic idea of this WZ video coding architecture is that the decoder, based on some previously and conventionally transmitted frames, the so-called key frames, creates the so-called SI which works as estimates for the other frames to code the so-called WZ frames. The WZ frames are then encoded using a channel coding approach, for example, with turbo codes or low-density parity-check (LDPC) codes, to correct the "estimation" errors in the corresponding decoder estimated side information frames. In this case, the encoding is performed assuming that there is (high) correlation between the original WZ frames to code and their associated SI frames at the decoder; the higher it is this correlation, the more efficient should be this encoding process. The Stanford WZ video codec [4] works at the frame level, uses turbo or low-density parity-check (LDPC) codes in the Slepian-Wolf codec and a feedback channel-based decoder rate control approach. In these WZ video codecs, the target quality is defined by means of the quantization parameters which are applied to the key frames and WZ frames DCT coefficients if a transform domain coding approach is used. This quality control is not very effective since the same quantization parameters may result in rather different quality levels depending on the video content characteristics, thus resulting in rather unstable quality evolutions.
Since the SI for the WZ coded frames is created at the decoder based on the conventionally encoded key frames, for example, using the H.264/AVC Intra standard, the rate-distortion (RD) of the WZ video codec strongly depends on the RD performance for the key frames, the quantization steps for the WZ frames DCT coefficients, and the accuracy of the SI estimate (which depends on the frame interpolation method used for the SI estimation). For the WZ video codecs currently available in literature, the quality of the key frames and WZ video frames is independently controlled typically using quantization parameters determined offline; thus, an overall reasonably constant quality can only be guaranteed, notably at shot level if some offline knowledge about the video content is previously acquired which is not a realistic solution; if a video sequence includes various shots with rather different content characteristics, the offline process becomes even more complex since the quantization parameters may have to be changed at shot level.
In this context, the main objective of this paper is to propose an efficient and effective quality control algorithm which allows reaching a rather uniform quality along time for both the key frames and WZ frames by dynamically adapting the key frames and WZ frames quantization parameters depending on the user target quality and the video content. This means that no previous offline knowledge needs to be acquired at all since the proposed algorithm allows to automatically and online following the content characteristics along time to reach a rather constant quality evolution; this implies that both real-time and offline applications may be targeted. The benchmarking for the proposed WZ video codec performance will be the RD performance and the quality variations obtained for the same codec when no quality control is performed. Comparisons will also be made with alternative relevant standard-based video codec solutions such as the H.264/AVC Intra and H.264/AVC No Motion codecs.
The rest of this paper is structured as follows. Section 2 reviews the background literature related to the problem addressed in this paper. Section 3 presents the Wyner-Ziv video codec used to implement, integrate, and evaluate the proposed quality control solution, in this case the IST transform domain WZ (IST-TDWZ) video codec. After introducing the proposed overall quality control system in Section 4, Section 5 presents the quality control solution proposed for the key frames while Section 6 presents the quality control solution proposed for the Wyner-Ziv frames. Afterwards, Section 7 gives the experimental results and performance analysis while Section 8 concludes this paper with some final remarks and perspectives for further work.
2. Reviewing the Related Literature
This section intends to review the existing literature related to the problem addressed in this paper this means quality control in WZ video coding. Since rate control is a problem very closely related to quality control, both types of solutions will be considered in this section. While there are a few solutions in literature addressing WZ coding with encoder rate control and one paper addressing quality control in the pixel domain, there is no single paper targeting the provision of constant quality for transform domain WZ video coding.
In [5], Morbée et al. propose an encoder rate allocation algorithm for a Stanford-like pixel domain WZ video codec. For this, the correlation between the decoder SI and the original WZ frame is estimated at the encoder by recreating the SI for each WZ frame as the average of the two temporally closer key frames. Furthermore, the bit-error probability of each bit plane is modeled assuming a binary symmetric channel (BSC). Based on some empirical data, an adequate model allows obtaining the number of bits to allocate to each bit plane and, thus, the overall rate. For sequences with medium and high motion, the proposed rate allocation algorithm overestimates the rate which results in a rather high RD performance loss.
A more recent encoder rate allocation solution is presented in [6] by Brites and Pereira, now in the context of a Stanford-like transform domain WZ video codec. While the overall coding architecture is similar to the one in [5] with the addition of the spatial transform, this paper introduces some more advanced tools. To estimate the correlation, a rough SI is created at the encoder using a fast motion compensation interpolating (FMCI) algorithm which allows getting more accurate side information estimation. Moreover, again based on empirical data, a model is derived to obtain a proper bit rate allocation at band level, for every bit plane, by computing the relative bit plane error probability and conditional entropy. With this approach, this solution reaches an RD performance which is typically above H.264/AVC Intra coding and similar to the usual decoder rate control for low and medium quality with low and medium motion content; for high-motion content, the RD losses may go down to about 1 dB.
Finally, Roca et al. propose in [7] a distortion control algorithm for a Stanford-like pixel domain WZ video codec. The target is to obtain a certain smooth quality over time both for the key frames and WZ frames. The proposed solution consists in two main modules: the first one provides distortion control for the key frames using a rather simple feedback-driven control structure while the second module estimates adequate quantization parameters for the WZ frames. In this solution, the noise correlation is estimated as in [5]. The main novelty is the proposed analytical model to estimate the WZ frames distortion using some statistical measures, taking into account the estimated correlation and the different quantization parameters. Finally, an exhaustive search determines the optimal quantization parameter, so that the estimated distortion is similar to the desired target distortion. Although the architecture allows providing a certain target distortion, the limitation of this method is mostly related to the statistical assumptions made, for example, a uniform distribution of the pixel values within a frame, as mentioned in the paper. Furthermore, the overall RD performance is below state-of-the-art WZ video codecs since the spatial redundancy is not exploited, for example, by using a spatial transform as in the transform domain WZ video codec adopted in this paper.
All rate/quality allocation methods presented above are similar in the sense that they use an encoder-derived model of the correlation noise between the SI and the WZ frame to determine the rate or the quantization parameters. These models are more or less complex depending on the empirical findings and the statistical assumptions made which usually limit the accuracy of the rate allocation or target quality. Since no quality control solution is available in literature for transform domain WZ video coding, this paper will propose an efficient and effective dynamic solution to guarantee a target uniform video quality for transform domain WZ video coding. As far as the authors know, this is the first solution tackling this problem.
3. The Basic Wyner-Ziv Video Codec
The IST-TDWZ video codec which will be used for this paper is based on the Stanford WZ video coding architecture presented in [4]. A very detailed performance evaluation of this type of WZ video codec is presented in [8].
The IST-TDWZ coding architecture illustrated in Figure 1 works as follows [8–10].
-
(1)
A video sequence is divided into WZ frames and key frames. Typically, a periodic coding structure is used with the group of pictures (GOPs) size defining the periodicity of the key frames; a GOP??= 2 means that there is one WZ frame for each key frame.
-
(2)
The key frames are coded using an efficient standard intracoding solution, for example, H.264/AVC Intra. The WZ frames are coded using a WZ coding approach; over each WZ frame, a
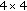 block-based discrete cosine transform (DCT) is applied.
block-based discrete cosine transform (DCT) is applied. -
(3)
The DCT coefficients of the entire WZ frame are grouped together, according to the position occupied by each DCT coefficient within the
 blocks, forming the DCT coefficients bands.
blocks, forming the DCT coefficients bands. -
(4)
Each DCT band is uniformly quantized with a (varying) number of levels, setting the quality target; however, content with different characteristics, for example, in term of motion, will still reach rather different objective and subjective qualities. This varying number of levels exploits the different sensibility of the human visual system to the various spatial frequencies.
-
(5)
Over the resulting quantization symbol stream, bit plane extraction is performed to form the bit plane arrays which are then independently turbo encoded.
-
(6)
The decoder creates the so-called side information (SI) for each WZ frame, which should be a good estimate of the original WZ frame [9], by performing a motion compensated frame interpolation process, using the previous and next decoded frames temporally closer to the WZ frame under coding.
-
(7)
A block-based
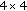 DCT is then carried out over the SI in order to obtain an estimate of the WZ frame DCT coefficients.
DCT is then carried out over the SI in order to obtain an estimate of the WZ frame DCT coefficients. -
(8)
The residual statistics between corresponding coefficients in the SI and the original WZ frame is assumed to be modeled by a Laplacian distribution which parameter is online estimated at the decoder.
-
(9)
The decoded quantization symbol stream associated to each DCT band is obtained through an iterative turbo decoding procedure for each bit plane. Whenever the estimated bit plane error probability is higher than a predefined threshold, typically
 , the decoder requests more parity bits from the encoder using the feedback channel. Because some residual errors are left even when the stopping criteria are fulfilled, and these errors have a rather negative subjective impact, an 8-bit cyclic redundancy check (CRC) sum technique [11] is used to confirm the successfulness of the decoding operation. If the CRC sum computed on the decoded bit plane does not match the check sum sent by the encoder, the decoder asks for more parity bits from the encoder buffer.
, the decoder requests more parity bits from the encoder using the feedback channel. Because some residual errors are left even when the stopping criteria are fulfilled, and these errors have a rather negative subjective impact, an 8-bit cyclic redundancy check (CRC) sum technique [11] is used to confirm the successfulness of the decoding operation. If the CRC sum computed on the decoded bit plane does not match the check sum sent by the encoder, the decoder asks for more parity bits from the encoder buffer. -
(10)
Once all decoded quantization symbol streams are obtained, the DCT coefficients are reconstructed using an optimal mean-squared error (MSE) estimate [12] in the sense that it minimizes the MSE of the reconstructed value, for each DCT coefficient, of a given band. A simpler, although less efficient, reconstruction solution also much used in literature, defines as the reconstructed value the side-information value, if this side information value in within the decoded bin; if not, the reconstructed value assumes the lowest intensity value or the highest intensity value within the decoded quantized bin, following a saturation approach. This simpler reconstruction solution bounds the error between the WZ frames and the reconstructed frames to the quantizer coarseness since the reconstructed pixel value is between the boundaries of the decoded quantized bin.
-
(11)
After all DCT coefficients bands are reconstructed, a block-based
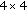 inverse discrete cosine transform (iDCT) is performed, and the decoded WZ frame is obtained.
inverse discrete cosine transform (iDCT) is performed, and the decoded WZ frame is obtained. -
(12)
To, finally, get the decoded video sequence, decoded key frames and WZ frames are conveniently mixed.
Naturally, a main target is to reach the best possible RD performance while applying the WZ video coding theoretical principles. In this process, the allocation of bits between the key frames and the WZ frames plays a central role in the final RD performance. For example, it is well known that the overall RD performance may be improved at the cost of a more nonuniform quality allocation between the key frames and the WZ frames which is typically not the best solution from the subjective quality point of view. To control the amount of bits necessary for the WZ frames, the WZ video coding architecture adopted here uses a feedback channel which allows the decoder to request the encoder the minimum amount of bits needed to improve the created SI to the quality target defined. The usage of a feedback channel has some implications, notably the limitation to real-time applications scenarios, the need to accommodate its associated delay, and the simplification of the rate control problem since the decoder, knowing the available side information, takes in charge the regulation of the necessary bit rate. To address this issue, some encoder rate control solutions, this means not needing the feedback channel, have already been proposed in literature for the same WZ video codec architecture [5, 6].
Regarding the quality control, and as far as the authors know, all transform domain WZ video codecs in literature simply use a set of predetermined quantization parameters to encode the H.264/AVC Intra key frames and the WZ frames DCT coefficients. This may allow reaching a reasonable smooth quality variation for sequences without long-term variations, if some offline processing is made to determine the key frames constant quantization parameter (QP) allowing to reach a quality similar to the quality obtained for each WZ frames quantization matrix (QM). Each of these QP and QM pairs defines an RD point with an associated average quality.
As mentioned before, this type of solution is very limited since
-
(i)
it does not allow providing any arbitrary constant target quality but only the qualities corresponding to the predefined quantization combinations;
-
(ii)
the decoded objective and subjective qualities will very much depend on the video content characteristics;
-
(iii)
the decoded objective and subjective qualities will only be stable as far as the content characteristics will be stable; for example, in a sequence with several shots, the quality may be rather stable within each shot but rather unstable between shots;
-
(iv)
it cannot work for applications scenarios where a priori knowledge is not available to define the adequate key frames QP for each WZ frames QM in order a smooth quality may be reached; thus, it cannot apply to real-time applications.
This main objective of this paper is thus to propose the first transform domain WZ video coding quality control solution overcoming the limitations listed above, this means allowing to reach any overall video quality level in a dynamic way without requiring any previous, offline analysis while providing the best possible RD performance; moreover, these objectives should be achieved without significantly changing the (low) encoding complexity features, typical of WZ video coding. For this, the WZ video encoder has to dynamically and online determine the QP and QM combinations allowing reaching a smooth quality while maximizing the RD performance.
4. Quality Control Algorithm: The Overall System
As stated above, the main objective of this paper is to propose an efficient quality control algorithm which allows reaching a rather uniform quality along time for both the key frames and WZ frames by dynamically adapting the key frames and WZ frames quantization parameters depending on the target quality and the video content. In this context, the only input is the target quality, for example, defined in terms of peak signal-to-noise ratio (PSNR) for each frame. This section intends to present the overall architecture of the proposed WZ video codec allowing global quality control for the key frames and WZ frames.
As it is shown in Figure 2, the proposed solution includes online quality control processing for both the key frames and WZ frames encoding parts of the WZ video codec. Basically, the overall technical approach considers four main modules.
-
(i)
Key frames quality control. Determines the key frames quantization parameters (QPs), for example, at frame level, in order that the desired target quality is reached with the minimum bit rate; for this, an adequate distortion model has to be used.
-
(ii)
H.264/AVC Intra encoder. Encodes the key frames using the QP determined by key frames quality control module; in this paper, the H.264/AVC Intra video codec has been selected since it is the most efficient video intracodec currently available.
-
(iii)
WZ frames quality control. Determines the quantization matrix (QM) for the DCT coefficients WZ frames in order that a rather smooth over time overall quality is obtained with the minimum rate; since the WZ frames RD performance strongly depends on the SI accuracy, which depends on the key frames quality, this process is not standalone in the sense that it depends not only on the WZ frames encoding but also on the key frames encoding.
-
(iv)
WZ frames encoder. Encodes the WZ frames using the QM determined by the WZ frames quality control module; for further explanations, the reader should consult Section 3.
The details on the key frames and WZ frames quality control modules will be presented in the next sections, starting with the key frames processing, which is standalone regarding the WZ frames coding; as mentioned above, the opposite is not true since WZ frames coding depends on the side information which is created based on the decoded key frames.
5. Key Frames Quality Control
The purpose of this section is to define an algorithm that allows encoding the key frames in the WZ video codec presented in Section 3 with a constant predefined quality. As usual in literature, and not withstanding the well-known limitations, the PSNR will be used here as the quality metric for quality control. Since the key frames are intraencoded, they do not depend on temporally adjacent frames, past or future and, thus, their quality is only dependent on the chosen QP for the transform coefficients. If there is a model available characterizing the relationship between the QP and the resulting quality/distortion, any video sequence can be intraencoded to reach a certain target quality, for example, in terms of PSNR, with the QP determined through that model.
In this section, a feedback-driven distortion-quantization (DQ) model is used to reach a certain constant target quality for the key frames while consuming the minimum rate. The DQ model here adopted is the one proposed in [13].
5.1. Architecture and Walkthrough
The key frames quality control architecture is presented in Figure 3. The main modules are the H.264/AVC Intra Encoder module, in this case implemented using the joint model 13.2 reference software [14], and the key frames quality control module which has the target to ensure a certain quality for the key frames while feeding the H.264/AVC Intra encoder with optimal QPs, in this case at macroblock level.
In a short walkthrough, the three novel processing modules in Figure 3 are now introduced.
-
(i)
DQ Model Parameters Estimation. Adopting a feedback-driven approach, the DQ model parameters (a and b, as it will be seen in the following) are determined using the QPs from the previously coded key frames as well as their resulting coding distortions.
-
(ii)
DQ Modeling. This block determines the QP for the next key frame to be encoded using the adopted DQ model. Therefore, it uses the updated model parameters (a and b) and the input target quality as reference.
-
(iii)
Macroblock (MB) Level QP Allocation. Since the DQ modeling module provides real QP values while the H.264/AVC Intra encoder has to be fed with integer QP values, this block determines an integer QP at macroblock level, in a way that the overall QP average at frame level is as close as possible to the value provided by the DQ modeling module.
5.2. Proposed Algorithm
After presenting the architecture and the basic approach for the key frames quality control algorithm, this section will introduce the proposed algorithm in detail.
5.2.1. Distortion-Quantization (DQ) Model
The most important element for the key frames quality control process is the DQ model. In [15] a quadratic DQ model theoretically derived from the rate-distortion theory is proposed for transform based-video codecs as

where a and b are the model parameters, QStep is the quantization step size, and D is the overall distortion after coding using the mean square error (MSE) as metric. In [13], this DQ model has been generalized to

in order to accommodate other types of DQ variations; this model has the advantage that parameter c is typically constant for each sequence, leading to a rather flexible model where only two (rather stable) parameters have to be estimated.
The DQ model (2) can be further refined by exploiting the H.264/AVC standard relation, where QStep doubles in value each six increments of QP [14] with QStep being the quantization step size and QP the quantization index. In this context, this relationship can be expressed by

Substituting (3) in (2), it results that

The model accuracy was assessed by intracoding a set of training sequences (Football at QCIF@15 Hz and Stefan and Tennis at QCIF@30 Hz) with different quantization parameters,  ; at the same time, the corresponding MSE distortion was measured, at frame level. In a second step, (4) was used as reference DQ model to fit the empirical data. Therefore, an offline nonlinear least squares estimation algorithm, the Levenberg-Marquardt algorithm [16] was used to estimate the three parameters a, b, and c for best curve fitting. Figure 4 presents the empirical distortion-quantization data for the Football sequence and the corresponding DQ model, using the estimated model parameters, this means
; at the same time, the corresponding MSE distortion was measured, at frame level. In a second step, (4) was used as reference DQ model to fit the empirical data. Therefore, an offline nonlinear least squares estimation algorithm, the Levenberg-Marquardt algorithm [16] was used to estimate the three parameters a, b, and c for best curve fitting. Figure 4 presents the empirical distortion-quantization data for the Football sequence and the corresponding DQ model, using the estimated model parameters, this means  ,
,  , and
, and  .
.
This experiment has shown that a good match exists between the real, empirical data and the adopted DQ model, if the right model parameters are used. To further test the model accuracy, the other two training sequences (Stefan and Tennis) were tested in the same way with similar conclusions. Comparing the standard derivation of the three model parameters a, b, and c, at frame level, within each sequence and between different sequences, it could be concluded that parameter c is very stable. Hence, it is possible to reduce the number of model parameters by keeping parameter  constant, without losing any significant accuracy; thus,
constant, without losing any significant accuracy; thus,  where this value corresponds to the overall mean from the sequences mentioned above. With just two parameters left, the complexity of the estimation method can be reduced from an iterative nonlinear least squares algorithm, notably the Levenberg-Marquardt algorithm, to a simpler linear least square algorithm. Thus, the DQ model (4) can be rewritten in a linearized form as
where this value corresponds to the overall mean from the sequences mentioned above. With just two parameters left, the complexity of the estimation method can be reduced from an iterative nonlinear least squares algorithm, notably the Levenberg-Marquardt algorithm, to a simpler linear least square algorithm. Thus, the DQ model (4) can be rewritten in a linearized form as

In this case, the remaining two model parameters a and b can be calculated with low computational effort and online updated using the knowledge from the past N key frames by substituting the expressions for x and y in (5) into (6)

5.2.2. DQ Model Parameters Estimation
Using the DQ model proposed above, the first step when coding each key frame consists in estimating the model parameters a and b using (6). Therefore, the knowledge from the past QP and the corresponding distortion in a temporal window with N frames size is used to estimate the new DQ model parameters. Experiments performed have shown that a window size of  is an adequate solution since it allows the quick adaptation to new sequence characteristics, while performing well in terms of PSNR smoothness.
is an adequate solution since it allows the quick adaptation to new sequence characteristics, while performing well in terms of PSNR smoothness.
5.2.3. DQ Modeling
After estimating the new DQ model parameters, the DQ model is used to determine the QP for the next key frame to be encoded. The DQ model is the one in (5), using already the updated model parameters a and b and the target quality D provided by the user in terms of MSE (after conversion from PSNR); as mentioned before,  . Since the DQ model provides a real-valued QP, the following step has to be applied to determine an integer QP as needed.
. Since the DQ model provides a real-valued QP, the following step has to be applied to determine an integer QP as needed.
5.2.4. Macroblock (MB) Level QP Allocation
Since the QP from the previous calculation is a real value and the H.264/AVC Intra encoder must be fed with integer values, some adequate QP processing has to be performed. Taking QP as an average at frame level, this last step ensures that a proper integer  is provided, at macroblock level, so that the average at frame level is as close as possible to the initially determined real QP.
is provided, at macroblock level, so that the average at frame level is as close as possible to the initially determined real QP.
For this, a simple solution is proposed where the frame is divided in two parts at macroblock level: top and bottom. The percentage ratio between these two parts depends on the fractional part of the real QP value: the top part corresponds to  % of the overall number of macroblocks in the frame and gets assigned
% of the overall number of macroblocks in the frame and gets assigned  , while the remaining macroblocks in the bottom part of the frame are quantized with
, while the remaining macroblocks in the bottom part of the frame are quantized with  ;
;  and
and  refer to the first integers higher and lower than x, respectively.
refer to the first integers higher and lower than x, respectively.
In summary, the method proposed above determines, for each key frame, at macroblock level, the QP to reach a certain selected quality at the minimum rate cost. In the following, the proposed solution considering both the H.264/AVC Intra encoder and key frames quality control modules will be called quality controlled H.264/AVC Intra encoder.
6. WZ Frames Quality Control
The main objective of this section is to define an algorithm that allows adjusting the QM for the WZ frames DCT coefficients to guarantee a similar quality, or distortion, compared to the key frames this means

where  and
and  are the local average distortions for the key frames and WZ frames, respectively. To reach this target, it is important to take into account that the key frames distortion is a function of the QP used for each key frame, defined to get a constant quality using the key frames quality control module presented above, while the WZ frames distortion itself is a function of both the QP of the adjacent key frames, used to create the corresponding SI, and the QM that is applied for the WZ frame in question (after the DCT transform).
are the local average distortions for the key frames and WZ frames, respectively. To reach this target, it is important to take into account that the key frames distortion is a function of the QP used for each key frame, defined to get a constant quality using the key frames quality control module presented above, while the WZ frames distortion itself is a function of both the QP of the adjacent key frames, used to create the corresponding SI, and the QM that is applied for the WZ frame in question (after the DCT transform).
The basic idea underpinning the proposed solution is to determine first, for each WZ frame, a target distortion at each DCT band level that is similar to the same band level distortion for its two temporal adjacent key frames; this should guarantee that the WZ frames and the key frames have an overall similar quality. After knowing which is the target distortion for each WZ frame DCT band, the QM with the number of quantization levels (QLs) for each DCT coefficient, guaranteeing that distortion when the WZ frame is coded and quantized, is estimated. For this, the distortion for each WZ frame DCT band is estimated as the coding error between the original WZ frame and the decoded WZ frame which depends on the statistics of the correlation noise and the reconstruction function used at the WZ decoder.
6.1. Architecture and Walkthrough
This section presented the WZ Frames Quality Control which has the target to ensure a certain quality for the WZ frames similar to the quality for the neighbor key frames. The WZ frames quality control architecture is presented in Figure 5: it gets input from an H.264/AVC Intra encoder with quality control used to encode the key frames (see Section 5). Furthermore, WZ transform domain coding is performed for the WZ frames using a proposed number of QLs for each DCT band.
In the following, a short description of the five main processing modules in the WZ frames quality control shown in Figure 5 will be presented.
-
(i)
Target distortion evaluation. Since the target distortion of the WZ frame to be coded should be similar to the key frames distortion, this module evaluates the distortion for the temporal adjacent key frames (already coded) at DCT band level.
-
(ii)
Rough side information (SI) estimation. This module performs, at the encoder side, a rough SI estimation using low-complexity interpolation techniques in order that the overall encoder complexity does not significantly change. This rough SI estimation, which should approximate the real decoder generated SI, is essential for the encoder to minimally know what will happen in terms of WZ decoding this means to model the correlation noise.
-
(iii)
Correlation noise modeling. Furthermore, the correlation noise between the approximated encoder generated SI and the original WZ frame is modeled at DCT band level by a Laplacian distribution; the variance
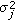 between the two frames at band level, an abstract expression of the SI fitness at band level, is passed to the WZ coding distortion estimation module.
between the two frames at band level, an abstract expression of the SI fitness at band level, is passed to the WZ coding distortion estimation module. -
(iv)
WZ coding distortion estimation. This module has the target to estimate the distortion of the WZ coded frames, at band level, for all possible QL values, using the computed variance
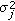 .
. -
(v)
WZ band quantization level determination. After the target distortion and the estimated distortions for the various QLs are known, an exhaustive search is performed, at band level, to determine the best match; this process provides the optimal QL for each coefficient band j this means the minimum number of quantization levels (and thus the minimum rate) allowing to reach the target distortion. This
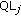 , one for each DCT band, will be passed to the WZ encoder to code the WZ frame in the usual WZ manner, overall reaching the desired target quality.
, one for each DCT band, will be passed to the WZ encoder to code the WZ frame in the usual WZ manner, overall reaching the desired target quality.
6.2. Proposed Algorithm
After presenting the global WZ frames quality control architecture, the WZ frames quality control algorithm to determine the QM for the WZ frames will be presented in detail in this section. In this process, it is assumed that the adjacent key frames have already been H.264/AVC intraencoded using the key frames quality control mechanism presented in Section 5. This allows guaranteeing a certain target quality, and thus a desired distortion, for the key frames as well as to provide the DCT-quantized coefficients to evaluate the corresponding band level distortion.
6.2.1. Target Distortion Evaluation
In this first step, the key frames distortion is evaluated at DCT band level. Since no key frame is available at the WZ frame position, the distortions of its two temporal adjacent key frames are averaged at band level to estimate the target distortion for the WZ frame. For a band level distortion evaluation, the (coded) key frames need to be transformed by applying an integer DCT like  transform as it happens when they are H.264/AVC encoded (which has already happened when they were H.264/AVC Intra coded). After that, the corresponding target distortion, for all 16 DCT bands, can be calculated as the weighted mean between the corresponding distortions for the two adjacent key frames. For each band j, the WZ frame target distortion based on the key frames
transform as it happens when they are H.264/AVC encoded (which has already happened when they were H.264/AVC Intra coded). After that, the corresponding target distortion, for all 16 DCT bands, can be calculated as the weighted mean between the corresponding distortions for the two adjacent key frames. For each band j, the WZ frame target distortion based on the key frames  at time t is computed as
at time t is computed as

where  are the original and
are the original and  the quantized key frame DCT coefficients for band j and time t. Taking this evaluated distortion based on the coded key frames as the target distortion for the WZ frame to be coded will allow guaranteeing that the key frames and the WZ frames have a similar overall distortion whatever the video content characteristics along time.
the quantized key frame DCT coefficients for band j and time t. Taking this evaluated distortion based on the coded key frames as the target distortion for the WZ frame to be coded will allow guaranteeing that the key frames and the WZ frames have a similar overall distortion whatever the video content characteristics along time.
6.2.2. Rough Side-Information Estimation
In order that the WZ encoder may later estimate the WZ-decoded quality, it is essential that it has some "idea" on the SI created at the decoder based on the decoded key frames. Since it is very undesirable to increase the encoder complexity as low-encoding complexity is a key benefit of WZ video coding, it is not acceptable to replicate at the encoder the same SI estimator used at the decoder; thus, a much simpler SI estimator is needed.
While a very simple SI estimation solution could be the average of the two temporal adjacent key frames, a more accurate solution, still with very low additional complexity, is the advanced fast motion-compensated interpolation (FMCI) proposed in [6] while defining an encoder rate control solution; in [6], it is stated that the FMCI, which is based on a very fast motion estimation algorithm, is less than 4 times more complex than a simple average interpolation. Experiments have proven that this SI estimation is acceptable for the purpose at hand since the absence of the original WZ frame (as it happens at the decoder) is more critical than the usage of a rough estimate of the real SI at the encoder, this from the noise modeling accuracy point of view.
6.2.3. Correlation Noise Modeling
The third step has the target to model the correlation noise n (or residue) at DCT band level between the decoder-generated SI and the original WZ frame. Usually, a Laplacian probability density function [10] is employed to statistically model the distribution of this correlation noise as

where  is the Laplacian distribution parameter.
is the Laplacian distribution parameter.
Since the original SI itself is only available at decoder, and this estimation is being made at the encoder, it is proposed here to make use of the encoder-computed rough SI to estimate the Laplacian parameter. Thereby, the variance  is computed as follows:
is computed as follows:

where B is the number of band j coefficients in the frame and  and
and  are the DCT coefficients for band j and time t for the WZ frame original and estimated SI coefficients, respectively.
are the DCT coefficients for band j and time t for the WZ frame original and estimated SI coefficients, respectively.
6.2.4. WZ Coding-Distortion Estimation
This step has the target to estimate, at the encoder, the distortion for the decoded WZ frames at DCT band level, this means after turbo decoding, and reconstruction at the decoder. This estimation is performed for all available  . Assuming a Laplacian model for the correlation noise,
. Assuming a Laplacian model for the correlation noise,  , the coding distortion between each reconstructed and original DCT band can be measured as
, the coding distortion between each reconstructed and original DCT band can be measured as

where  is an estimation of the MSE optimal-reconstructed coefficient [12] at the decoder for band j at time t
is an estimation of the MSE optimal-reconstructed coefficient [12] at the decoder for band j at time t

where LB and UB are the lower and upper bounds of the quantization interval for the DCT coefficients using  for the band j in question, and offset and adjustment are determined by the optimal reconstruction process; further details are presented in [12].
for the band j in question, and offset and adjustment are determined by the optimal reconstruction process; further details are presented in [12].
Compared to the simpler reconstruction function [4] mentioned in Section 3, the reconstruction function in (12) shifts the reconstruction levels toward the center of the quantization interval. Since the reconstructed DCT coefficient will be forced to be in between the boundaries in (12), its accuracy highly depends on the quantization coarseness, this means on the number of quantization levels used; thus, for a higher QL value, the expectable distortion will decrease and viceversa.
Since (11) cannot be analytically solved while using the reconstruction in (12), two alternative solutions are possible: (i) to use a numerical solution for (11) with the risk to significantly increase the encoding complexity which is not desirable for WZ video coding; (ii) to approximate the optimal reconstruction (12) with the simpler reconstruction described in Section 3 [4] which allows an analytical solution for (11) and does not significantly increase the encoding complexity as requested; in this case, the reconstructed DCT coefficient would be

Considering the critical low-complexity requirement, it is proposed here to adopt the second solution. Thus, substituting (9) in (11) and replacing  with
with  the integral in (11) can be analytically solved resulting in
the integral in (11) can be analytically solved resulting in

It should be noticed that, inside a DCT band, equal coefficients appear many times which thus lead to the same single coefficient distortion. In this case, to reduce the complexity, instead of summing up over all coefficient distortions in (14) to obtain the overall DCT band distortion, it is possible to sum up only the "unique" coefficient distortions and multiply each of them by their occurrence.
6.2.5. WZ Band Quantization Level Determination
Finally, the adequate QL for each band j is determined by identifying the value  for which the WZ-estimated distortion is the closest, but higher, regarding the WZ target distortion already evaluated:
for which the WZ-estimated distortion is the closest, but higher, regarding the WZ target distortion already evaluated:

Since the key frames have a more important role in the overall RD performance than the WZ frames as they determine the quality of the side information, (15) gives a distortion priority to the key frames (this means its quality is never lower than the estimated WZ frames quality).
Initially, the distortion  is obtained from step A. After, step D is executed in an iterative loop for all available
is obtained from step A. After, step D is executed in an iterative loop for all available  starting from the lowest or the highest value depending on the PSNR target to reduce the associated complexity. As soon as criteria (15) fulfilled, the iteration process stops and the corresponding
starting from the lowest or the highest value depending on the PSNR target to reduce the associated complexity. As soon as criteria (15) fulfilled, the iteration process stops and the corresponding  can be taken as the optimal number of quantization levels for the WZ frame coefficients in band j.
can be taken as the optimal number of quantization levels for the WZ frame coefficients in band j.
7. Performance Evaluation
This section presents the performance obtained for the quality control algorithm proposed in the previous sections.
7.1. Test Conditions
Before presenting the performance obtained, the test conditions used are precisely defined, notably.
-
(i)
Test sequences. Concatenation of a set of sequences, notably Foreman (with the Siemens logo), Hall Monitor, and Coast Guard, this means Foreman for frames 1 to 150, Hall Monitor for frames 151 to 315, and Coast Guard for frames 316 to 465; these sequences represent different types of content and are all different from the training sequences used before. No performance results are presented for individual sequences as this would correspond to an easier case since within each sequence there are typically much less variations than in the concatenation of a set of sequences such as the one described above. Since what is difficult in the problem addressed is to overcome high-content variations, the concatenated sequence should show better the quality control capabilities of the proposed solution.
-
(ii)
Frames for each sequence. All frames; this means 150 frames for Foreman, 165 frames for Hall Monitor, and 150 frames for Coast Guard (one sample frame of each test sequence at 15?Hz is shown in Figure 6).
-
(iii)
Spatial and temporal resolution. QCIF at 15?Hz (this means 7.5?Hz for the WZ frames as GOP??= 2 is always used in this paper); it is important to notice that many results in literature use a QCIF@30?Hz combination which allows to get much better WZ video coding RD performance although less relevant from a practical applications point of view.
-
(iv)
Bit rate and PSNR. As usual for WZ video coding, only the luminance component of each frame is used to compute the overall bit rate and PSNR which always considers both the key frames and WZ frames.
-
(v)
WZ frames quantization. Different RD performance can be achieved by changing the quantization matrix values (QM) for the WZ frames DCT coefficients, thus defining different RD points. When no quality control as proposed in this paper is performed, the eight rate-distortion points corresponding to the
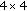 QM depicted in Figure 7 are used. Within a
QM depicted in Figure 7 are used. Within a  QM, each value indicates the number of quantization levels, QLs, associated to the corresponding DCT coefficient; the value 0 means that the corresponding coefficient is not coded and, thus, no Wyner-Ziv bits are transmitted for that band (instead the SI value is taken for the reconstruction process). In the following, the various matrices will be referred as
QM, each value indicates the number of quantization levels, QLs, associated to the corresponding DCT coefficient; the value 0 means that the corresponding coefficient is not coded and, thus, no Wyner-Ziv bits are transmitted for that band (instead the SI value is taken for the reconstruction process). In the following, the various matrices will be referred as  with
with  ; when i increases, the bit rate and the quality also increase.
; when i increases, the bit rate and the quality also increase. -
(vi)
Key frames quantization. When no quality control is performed as proposed in this paper, the key frames are quantized with a constant QP (see Table 1) which allows reaching an average quality similar to the WZ frames average quality. Although this option does not maximize the overall RD performance (this would require benefiting the key frames in rate and quality), it corresponds to a more relevant practical solution from the user perspective since a smoother quality variation is provided, improving the subjective quality impact.
The following video codecs will be used as benchmarks for the evaluation of the proposed WZ video codec with quality control.
-
(i)
WZ video codec without quality control. Coding with the IST-TDWZ video codec introduced in Section 3; the RD points correspond to the eight
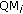 defined above in Figure 7 for the WZ frames and to the QP defined in Table 1 for the key frames.
defined above in Figure 7 for the WZ frames and to the QP defined in Table 1 for the key frames. -
(ii)
H.264/AVC Intra. Coding with H.264/AVC in main profile using a constant QP without exploiting any temporal redundancy (I-I-I
 ); H.264/AVC is considered the most efficient standard intra-coding available.
); H.264/AVC is considered the most efficient standard intra-coding available. -
(iii)
H.264/AVC Inter no motion. Coding with H.264/AVC in main profile using a constant QP and exploiting the temporal redundancy with an I-B
 I-B
I-B prediction structure but without performing any motion estimation which is the most computationally expensive encoding task.
prediction structure but without performing any motion estimation which is the most computationally expensive encoding task.
It will be important to notice that the benchmarking solutions above do not provide the quality control features that the proposed quality control algorithm does, independently of the video content.
The next sections will present and discuss the performance of the proposed quality control mechanism.
7.2. Performance Results: Key Frames Quality Control
This section intends to report the performance of the key frames quality control mechanism proposed in Section 5. To better evaluate the obtained quality smoothness, a rather inhomogeneous sequence such as the concatenation of video sequences described in the test conditions above will be used.
Figure 8 shows the temporal PSNR variation for the key frames coded without any quality control for three different constant QP values (30, 36, and 42) while Figure 9 shows the PSNR variation when the proposed key frames quality control mechanism is used with a target PSNR quality similar to the average PSNR obtained for the QP values used in Figure 8. In Figure 8, the resulting PSNR exhibits considerable PSNR fluctuations within each sequence and especially across sequences. In contrast, the proposed key frame quality control (Figure 9) allows reaching a rather smooth and stable PSNR quality with small variations, apart from some few higher quality local variations, notably at scene changes. These local variations should be rather imperceptible in terms of the user subjective impact while the same would not happen for the significant average quality changes.
Table 2 shows the average PSNR, the PSNR variance, and the bit rate for the two scenarios mentioned above, this means key frames codec with and without quality control, for the same average PSNR. Besides showing the significant PSNR variance reduction obtained with the proposed quality control mechanism, Table 2 also shows that this reduction comes at the cost of some compression efficiency since the rate is slightly higher; notably, the bit rate increases up to 6% for the same PSNR or the PSNR decreases around 0.4 dB for the same rate, respectively. This small RD performance reduction is also shown in Figure 10, thus confirming that the significant additional quality smoothness has a (rather small) price in terms of RD performance.
In summary, it may be concluded that the proposed key frame quality control solution allows targeting a certain video quality with rather limited PSNR variations in comparison with a fixed QP solution. Moreover, it allows to effectively target any quality defined in terms of PSNR or MSE while a fixed QP solution may result in rather different average qualities along a video sequence depending on its characteristics.
7.3. Performance Results: Overall Quality Control
This section intends to report the performance of the proposed overall quality control solution this means the integration of the key frames quality control and the WZ frames quality control mechanisms proposed above. The performance will be assessed in terms of PSNR variance and compression efficiency for the two scenarios already used in the previous section, this means WZ video coding with and without quality control.
Figure 11 illustrates the temporal PSNR variation for the concatenated test sequence coded without quality control for two RD points as defined above, notably  and
and  . Moreover, Figure 12 shows the temporal PSNR variation using the proposed quality control mechanism for both the key and WZ frames, for the same concatenated test sequence, using as target quality the average PSNR resulting from the without quality control coding cases in Figure 11 (29.25 and 32.28 dB). An additional quality level is also included which is below the lowest quality that can be reached when using the eight RD points defined above for WZ coding without quality control, thus showing the flexibility and capability of the proposed method to achieve any desired average PSNR with very low temporal variations.
. Moreover, Figure 12 shows the temporal PSNR variation using the proposed quality control mechanism for both the key and WZ frames, for the same concatenated test sequence, using as target quality the average PSNR resulting from the without quality control coding cases in Figure 11 (29.25 and 32.28 dB). An additional quality level is also included which is below the lowest quality that can be reached when using the eight RD points defined above for WZ coding without quality control, thus showing the flexibility and capability of the proposed method to achieve any desired average PSNR with very low temporal variations.
The temporal PSNR variation in Figure 11 for the scenario without quality control, this means using predefined QM and QP, is characterized by substantial quality fluctuations. Since the coding parameters, a priori adopted (e.g., see Table 1), target a similar average quality for the key frames and WZ frames within each sequence concatenated, they are not able to adapt to the more local content variations as the video sequence exhibits nonsteady-state signal characteristics. Moreover, the reader should notice that a priori knowledge on the global average is not available in a real-time scenario and thus, in practice, these QPs are not available.
In contrast, Figure 12 shows that the quality control mechanism allows reaching a certain target PSNR for both the key frames and WZ frames with minor quality variations, notably a rather uniform quality along time also across sequences. Moreover, this type of solution does not require any a priori knowledge of the video content in order to reach a certain smooth quality since it automatically adapts to any video characteristics. Furthermore, it is now possible to provide any desired quality which was not possible using only predefined parameter sets.
Table 3 compares several coding statistics for the two alternative WZ video coding methods—with and without quality control—for the same average PSNR. As can be seen from the results, the proposed solution allows to smoothly keeping a certain target quality as shown by the lower PSNR variance, thus improving the user visual experience. Again, there is a small RD performance cost associated to the smoother quality case.
To evaluate the overall RD performance of the proposed quality-controlled WZ video codec regarding standard video codecs with similar low encoding complexity, Figure 13 shows the RD performance of four alternative codecs: the H.264/AVC Intra codec which only exploits the spatial correlation, the H.264/AVC No Motion codec which exploits the spatial and temporal correlations but without motion compensation, the IST-TDWZ codec without quality control, and the IST-TDWZ codec with quality control. These codecs are comparable in the sense that they all ask for a rather similar low encoding complexity (all without motion estimation).
While it may be concluded that the IST-TDWZ codec with quality control has an RD performance loss of about 0.4 dB regarding the WZ coding solution without quality control (using the predefined quantization parameters), it may also be concluded that it outperforms H.264/AVC Intra by about 2 dB at lower rates and about 1 dB at higher rates. This shows that WZ video coding may already provide interesting coding solution for applications requiring low-complexity encoding since RD performance gains regarding the H.264/AVC Intra codec are already possible even for a rather constant quality. Regarding, the H.264/AVC No Motion benchmarking, the proposed quality control solution achieves a similar quality for the lower bit rates but still shows an RD performance gap of almost 1 dB for the higher bit rates. It is expected that this RD performance gap will be reduced in the future with further research on WZ video coding. Still, it is important to stress already at this stage that the H.264/AVC No Motion solution shows a much higher PSNR variance than the proposed quality-controlled WZ video coding solution which may not be adequate for certain applications; moreover, the WZ video coding solution will be more resilient to error propagation.
It is important to notice that the small RD performance penalty of the quality-controlled WZ video codec regarding the WZ video codec without quality is compensated by its robustness to large variations of the video sequence characteristics as it may happen in real scenarios, for example, video surveillance in varying lighting conditions, camera pannings and zoomings and varying number of monitored persons. This quality control capability broadens the spectrum of WZ video coding promising applications to all areas where the video characteristics are changing and unknown in advance, while still requiring low encoding complexity.
7.4. Performance Results: Overall Encoding Complexity
In [8], it is stated that the IST-TDWZ video codec encoding complexity (without quality control) is about 50–70% of the encoding complexity of the most relevant standard-based alternative solutions, notably H.264/AVC Intra and H.264/AVC No Motion, for GOP size 2; this percentage will be even much smaller for longer GOP sizes. Since low encoding complexity is a critical requirement for WZ video coding, it was requested in Section 4 that the proposed quality control mechanism should not significantly increase the encoding complexity. Coding experiments performed using an Intel Quad Core 2,66 GHz PC with 4 GB RAM running Windows XP SP3 (no parallel code execution) have shown that the proposed quality control solution only increases the encoding complexity as much as 10% for the lower QM while 4-5% increases are more common. These figures allow concluding that the proposed quality control solution does not significantly change the status quo in terms of encoding complexity.
8. Conclusions and Further Work
This paper proposes an efficient and dynamic quality control mechanism to ensure a certain constant video quality over time for a transform domain Wyner-Ziv video codec. Using this solution, any constant target quality may be reached for the overall video, without any previous knowledge or offline processing, this means also for real-time applications where the sequence characteristics are unknown in advance. This smooth quality variation comes at a rather small cost in RD performance regarding the alternative solution without quality control and, thus, with much stronger quality variations. Moreover, there are significant RD performance gains regarding H.264/AVC Intra coding with additional advantages in encoding complexity. Because the feedback channel is not used for the quality control process, all additional computations are performed at the encoder without any significant increase in terms of encoding complexity.
The proposed solution may be further improved by implementing a more granular modeling of the key frame distortion, for example, at macroblock level. Moreover, it should be possible to derive an analytical DQ model for the WZ frames as it is already used for the key frames because the QL values for each band are analytically determined. Finally, the WZ video codec may adopt an encoder rate control solution because the feedback channel is not needed at all and new application scenarios may be addressed.
References
Slepian D, Wolf J: Noiseless coding of correlated information sources. IEEE Transactions on Information Theory 1973,19(4):471-480. 10.1109/TIT.1973.1055037
Wyner A, Ziv J: The rate-distortion function for source coding with side information at the decoder. IEEE Transactions on Information Theory 1976,22(1):1-10. 10.1109/TIT.1976.1055508
Pereira F, Torres L, Guillemot C, Ebrahimi T, Leonardi R, Klomp S: Distributed Video Coding: selecting the most promising application scenarios. Signal Processing: Image Communication 2008,23(5):339-352. 10.1016/j.image.2008.04.002
Girod B, Aaron AM, Rane S, Rebollo-Monedero D: Distributed Video Coding. Proceedings of the IEEE 2005,93(1):71-83.
Morbée M, Prades-Nebot J, Pižurica A, Philips W: Rate allocation algorithm for pixel-domain distributed video coding without feedback channel. Proceedings of IEEE International Conference on Acoustics, Speech, and Signal Processing (ICASSP '07), April 2007, Honolulu, Hawaii, USA 1: 521-524.
Brites C, Pereira F: Encoder rate control for transform domain Wyner-Ziv video coding. Proceedings of the 14th IEEE International Conference on Image Processing (ICIP '07), September-October 2007, San Antonio, Tex, USA 2: 5-8.
Roca A, Morbée M, Prades-Nebot J, Delp EJ: A distortion control algorithm for pixel-domain Wyner-Ziv video coding. Proceedings of the Picture Coding Symposium (PCS '07), November 2007, Lisbon, Portugal 1-4.
Brites C, Ascenso J, Pedro JQ, Pereira F: Evaluating a feedback channel based transform domain Wyner-Ziv video codec. Signal Processing: Image Communication 2008,23(4):269-297. 10.1016/j.image.2008.03.002
Ascenso J, Brites C, Pereira F: Content adaptive Wyner-Ziv video coding driven by motion activity. Proceedings of the Intentional Conference on Image Processing (ICIP '06), October 2006, Atlanta, Ga, USA 605-608.
Brites C, Ascenso J, Pereira F: Improving transform domain Wyner-Ziv video coding performance. Proceedings of IEEE International Conference on Acoustics, Speech, and Signal Processing (ICASSP '06), May 2006, Toulouse, France 2: 525-528.
Kubasov D, Lajnef K, Guillemot C: A hybrid encoder/decoder rate control for Wyner-Ziv video coding with a feedback channel. Proceedings of the 9th IEEE International Workshop on Multimedia Signal Processing (MMSP '07), October 2007, Crete, Greece 251-254.
Kubasov D, Nayak J, Guillemot C: Optimal reconstruction in Wyner-Ziv video coding with multiple side information. Proceedings of the 9th IEEE International Workshop on Multimedia Signal Processing (MMSP '07), October 2007, Crete, Greece 183-186.
Nunes P: Rate control for object-based video coding, Ph.D. thesis. Instituto Superior Técnico, Technical University of Lisbon, Lisbon, Portugal; July 2007. http://www.img.lx.it.pt
H.264/AVC Reference Software Version JM 13.2, http://iphome.hhi.de/suehring/tml
Hang H-M, Chen J-J: Source model for transform video coder and its application—part I: fundamental theory. IEEE Transactions on Circuits and Systems for Video Technology 1997,7(2):287-298. 10.1109/76.564108
Ranganathan A: The Levenberg-Marquardt Algorithm. June 2004, http://www.cc.gatech.edu/~ananth/docs/lmtut.pdf
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License ( https://creativecommons.org/licenses/by/2.0 ), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Sofke, S., Pereira (EURASIP Member), F. & Müller, E. Dynamic Quality Control for Transform Domain Wyner-Ziv Video Coding. J Image Video Proc 2009, 978581 (2009). https://doi.org/10.1155/2009/978581
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1155/2009/978581
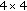 block-based discrete cosine transform (DCT) is applied.
block-based discrete cosine transform (DCT) is applied. blocks, forming the DCT coefficients bands.
blocks, forming the DCT coefficients bands.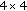 DCT is then carried out over the SI in order to obtain an estimate of the WZ frame DCT coefficients.
DCT is then carried out over the SI in order to obtain an estimate of the WZ frame DCT coefficients. , the decoder requests more parity bits from the encoder using the feedback channel. Because some residual errors are left even when the stopping criteria are fulfilled, and these errors have a rather negative subjective impact, an 8-bit cyclic redundancy check (CRC) sum technique [
, the decoder requests more parity bits from the encoder using the feedback channel. Because some residual errors are left even when the stopping criteria are fulfilled, and these errors have a rather negative subjective impact, an 8-bit cyclic redundancy check (CRC) sum technique [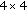 inverse discrete cosine transform (iDCT) is performed, and the decoded WZ frame is obtained.
inverse discrete cosine transform (iDCT) is performed, and the decoded WZ frame is obtained.




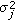 between the two frames at band level, an abstract expression of the SI fitness at band level, is passed to the WZ coding distortion estimation module.
between the two frames at band level, an abstract expression of the SI fitness at band level, is passed to the WZ coding distortion estimation module.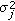 .
.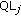 , one for each DCT band, will be passed to the WZ encoder to code the WZ frame in the usual WZ manner, overall reaching the desired target quality.
, one for each DCT band, will be passed to the WZ encoder to code the WZ frame in the usual WZ manner, overall reaching the desired target quality.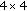 QM depicted in Figure
QM depicted in Figure  QM, each value indicates the number of quantization levels, QLs, associated to the corresponding DCT coefficient; the value 0 means that the corresponding coefficient is not coded and, thus, no Wyner-Ziv bits are transmitted for that band (instead the SI value is taken for the reconstruction process). In the following, the various matrices will be referred as
QM, each value indicates the number of quantization levels, QLs, associated to the corresponding DCT coefficient; the value 0 means that the corresponding coefficient is not coded and, thus, no Wyner-Ziv bits are transmitted for that band (instead the SI value is taken for the reconstruction process). In the following, the various matrices will be referred as  with
with  ; when i increases, the bit rate and the quality also increase.
; when i increases, the bit rate and the quality also increase.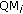 defined above in Figure
defined above in Figure  ); H.264/AVC is considered the most efficient standard intra-coding available.
); H.264/AVC is considered the most efficient standard intra-coding available. I-B
I-B prediction structure but without performing any motion estimation which is the most computationally expensive encoding task.
prediction structure but without performing any motion estimation which is the most computationally expensive encoding task.






