- Research Article
- Open access
- Published:
Error Resilience in Current Distributed Video Coding Architectures
EURASIP Journal on Image and Video Processing volume 2009, Article number: 946585 (2009)
Abstract
In distributed video coding the signal prediction is shifted at the decoder side, giving therefore most of the computational complexity burden at the receiver. Moreover, since no prediction loop exists before transmission, an intrinsic robustness to transmission errors has been claimed. This work evaluates and compares the error resilience performance of two distributed video coding architectures. In particular, we have considered a video codec based on the Stanford architecture (DISCOVER codec) and a video codec based on the PRISM architecture. Specifically, an accurate temporal and rate/distortion based evaluation of the effects of the transmission errors for both the considered DVC architectures has been performed and discussed. These approaches have been also compared with H.264/AVC, in both cases of no error protection, and simple FEC error protection. Our evaluations have highlighted in all cases a strong dependence of the behavior of the various codecs to the content of the considered video sequence. In particular, PRISM seems to be particularly well suited for low-motion sequences, whereas DISCOVER provides better performance in the other cases.
1. Introduction
Distributed video coding (DVC) is attracting some attention due to the potential innovative application perspectives with respect to the more traditional approaches (see, e.g., [1]). DVC is based on the principles of distributed source coding (DSC), a branch of information theory introduced in the 70s by Slepian and Wolf [2] and Wyner and Ziv [3], which have been applied to the transmission of a video sequence. The main idea of DVC attempts to exploit the temporal correlation of a video signal in the decoding phase rather than in the encoding one. In this way, the classic motion compensated prediction is not performed any longer at the encoder, with a consequent significant reduction in the computational complexity of the encoder. DSC principles are used instead. The encoding rate is reduced by transmitting only the parity bits of a suitable systematic channel code, which are extracted from the original frames that need to be sent. At the decoder, the redundancy of the video sequence is taken into account by performing a motion compensated prediction based on the already received data, and the received parity bits are then used to recover as much as possible the original information from a motion compensated signal generated at the decoder. The reason for using such an approach is manyfold. A first motivation is that in DVC there is a shift of the computational complexity from the encoder to the decoder. The decoding phase requires in fact quite complex operations that are conceptually and computationally analogous to the motion estimation performed by an encoder in the traditional video coding schemes. On another hand, only very simple computations can occur at the encoder. For this reason, DVC is particularly suited for applications that requires very simple, cheap, and low-power encoding.
A second expected advantage of DVC is related to the intrinsic ability to cope with transmission errors. In fact, given that no prediction loop is used in the encoding phase, the distributed coding scheme should be more resilient to channel errors since it is not affected by the typical drift problems which may occur in traditional predictive systems.
While the advantages in terms of reduced computational complexity may be partially mitigated by hardware technological advances, the expected intrinsic error resilience may turn out to be an attractive aspect in the application scenarios prone to continuously varying channel characteristics, for which traditional FEC (forward error correcting codes) fails to be effective.
In literature, various papers addressing the possible applications of DVC schemes to improve the error resilience of a video codec have been presented. For example, in [4, 5] Wyner-Ziv coding is used to generate a supplementary bitstream able to improve the error protection performance on H.264/AVC compliant video coding schemes.
In [6, 7] a first evaluation of the error resilience properties of a Stanford-based codec and a first comparison with H.264/AVC have been presented and discussed. In this paper we are extending the scope of the previously proposed treatments by presenting the error resilience capabilities of two video codecs based on the two main DVC architectures proposed in literature, namely, we consider a video codec based on the Stanford architecture, proposed in [8–10], and a video codec based on the PRISM architecture, described in [11, 12]. The Stanford-based codec has been further refined within the DISCOVER European funded project [13]. Specifically, an accurate temporal and rate/distortion-based evaluation of the effects of the errors for both the considered DVC architectures has been performed and discussed. To complete the evaluation, a further performance comparison of both schemes with respect to H.264/AVC standard video codec [14] has been carried out. Moreover, we have also performed a theoretical evaluation of the errors propagation in case of traditional predictive schemes and in case of DVC.
In more detail, the performance evaluation has been carried out as follows.
-
(i)
Temporal analysis in presence of channel errors. Determine the effects of transmission errors by analyzing the frame-by-frame PSNR evolution at a given bit rate, to determine the effects of such transmission errors for both coding architectures.
-
(ii)
Rate/distortion analysis in presence of channel errors for different packet loss rates (PLR). Measurements of the rate/distortion responses when no FEC error protection are considered. Specifically we have compared the results obtained using the DISCOVER codec, the PRISM codec and one configuration of H.264/AVC, with GOP2 in IBIB mode.
-
(iii)
Rate/distortion analysis in presence of channel errors and FEC protection for different PLR. Measurements of the PSNR responses obtained by the DISCOVER codec with respect to those obtained by H.264/AVC with a GOP8 are considered, while adopting an FEC protection so as to partially cope with transmission errors up to a certain PLR.
The paper is organized as follows. In Section 2, a distributed source coding example is provided to show the theoretical intrinsic robustness in presence of channel errors for sources with memory. In Section 3, a reference to the state of the art for transmission error protection is given specifically for the framework of distributed video coding. Section 4 describes the 2 DVC architectures considered in this paper, whereas in Section 5 the experimental results are conducted. Concluding remarks are given in Section 6.
2. Intrinsic Error Resilience in Distributed Source Coding
To give an idea of the intrinsic error resilience of distributed source coding, in this section we present a simple explicative example. In this example, a predictive and a distributed coding systems are compared in terms of resilience to channel errors.
The considered coding systems have been introduced in the well-known DSC explicative example reported for instance in [15, 16]. Whereas in the reference example the coding of two correlated random variables is considered, in our example we consider the coding of a sequence of random variables  . As proposed in the reference example, it is assumed that
. As proposed in the reference example, it is assumed that  is a
is a  bit random variable and that
bit random variable and that  can differ from
can differ from  in at most
in at most  bit.
bit.
The considered predictive coding system is reported in Figure 1. For every  , the prediction residue
, the prediction residue  is sent. Since there are
is sent. Since there are  admissible values for
admissible values for  ,
,  bits are needed for
bits are needed for  to be encoded. In Table 1 a realization of
to be encoded. In Table 1 a realization of  and its transmission over an error-prone channel is reported, in order to show the impact of a channel error. Since the decoding consists in adding the prediction residue to the previously decoded variable, the error in
and its transmission over an error-prone channel is reported, in order to show the impact of a channel error. Since the decoding consists in adding the prediction residue to the previously decoded variable, the error in  propagates throughout the sequence, and therefore from
propagates throughout the sequence, and therefore from  on, every reconstructed variable will contain
on, every reconstructed variable will contain  errors.
errors.
On the other hand, when  is encoded in a distributed fashion, the behavior in presence of channel errors is completely different. In Figure 2, the distributed coding scheme introduced in the reference example is reported. The
is encoded in a distributed fashion, the behavior in presence of channel errors is completely different. In Figure 2, the distributed coding scheme introduced in the reference example is reported. The  admissible values for
admissible values for  are divided into
are divided into  cosets and, for every
cosets and, for every  , the corresponding
, the corresponding  bit coset index is sent. Since the code structure is such that one word only in each coset is at distance at most
bit coset index is sent. Since the code structure is such that one word only in each coset is at distance at most  from any fixed word, in absence of transmission errors the decoder can always identify
from any fixed word, in absence of transmission errors the decoder can always identify  based on the knowledge of
based on the knowledge of  . Table 2 shows the decoding of a sequence affected by a channel error of
. Table 2 shows the decoding of a sequence affected by a channel error of  bit. It can be observed that, in spite of the decoding error in position
bit. It can be observed that, in spite of the decoding error in position  , the reconstructed sequence, from position
, the reconstructed sequence, from position  on, is correct. The mechanisms of distributed coding have prevented the error propagation. This is mainly due to the fact that the encoding of
on, is correct. The mechanisms of distributed coding have prevented the error propagation. This is mainly due to the fact that the encoding of  does not depend on the value of
does not depend on the value of  , so it is possible to infer the right value of
, so it is possible to infer the right value of  even if the side information is uncorrect.
even if the side information is uncorrect.
It is important to notice that, in some cases, for instance the one reported in Table 3 it is impossible for the decoder to compensate for a transmission error, and it therefore propagates throughout the stream. This is due to the fact that in this system the innovation between  and
and  is
is  bit, so the coding rate exactly equals its bound, and no redundancy margin remains for the entropy introduced by channel errors.
bit, so the coding rate exactly equals its bound, and no redundancy margin remains for the entropy introduced by channel errors.
Modifying the initial hypothesis and assuming that the difference between  and
and  is exactly
is exactly bit, it is possible to avoid error propagation in all cases. In Table 4 decoding under this assumption is shown. In this case the encoding rate (
bit, it is possible to avoid error propagation in all cases. In Table 4 decoding under this assumption is shown. In this case the encoding rate ( bits) exceeds the innovation entropy (
bits) exceeds the innovation entropy ( bit). Anyway, the predictive system could not exploit the same amount of redundancy to protect the encoded stream: at most
bit). Anyway, the predictive system could not exploit the same amount of redundancy to protect the encoded stream: at most  transmission error could be therefore detected but not corrected.
transmission error could be therefore detected but not corrected.
3. Related Works
The reliable transmission of compressed video signal over an error prone network is an important research topic. Best effort packet-based transmission over networks, which do not ensure that all sent packets are correclty received, are the most widespread nowadays. This implies that suitable procedures capable to deal with missing information at the receiver are essential. The problem of transmission errors becomes even more challenging in the case of wireless networks, since the channel becomes less reliable and bandwidth constraints are stronger.
To appreciate the use of DVC as a method for improving the error resilience capabilities of a video codec, some basic notions on the topic are required, and are thus briefly reported in this section. A detailed discussion concerning the transmission of the video signal over unreliable channels is however out of the scope of the present paper, and the interested reader can find a more detailed discussion, for example, in [17].
In order to protect the transmitted data, FEC has usually been employed. Since FEC tends to be quite expensive in terms of bandwidth, a lot of techniques aimed at achieving the best trade-off between FEC overhead and effective data protection in terms of error recovery have been proposed. In this field, the most widespread techniques are based on unequal FEC, that is, different portions of compressed data elements (e.g., H.264/AVC stream) are not allocated the same amount of redundancy bits. On the contrary, more redundancy is assigned to those parts of the stream that are considered to be most important for an acceptable decoding quality of the received signal. For example, syntactic headers have to be almost error-free to avoid decoder crashes, while data symbols can tolerate some errors. Techniques for unequal error protection (UEP) can be found, for example, in [18–21].
Since it is impossible to avoid any loss of data packets, it becomes necessary to compensate in some way the data that the decoder has not received. In the literature, several approaches have been proposed in order to achieve good concealment strategies for the lost data. In particular in traditional predictive video coding, the H.264/AVC standard is endowed with many tools and features that have been specifically designed to improve the error resilience performance, and to conceal as precisely as possible the missing information. For example the flexible macroblock ordering (FMO) tool allows to divide an H.264/AVC picture in non regular slices, and to choose dynamically the macroblocks belonging to each slice. Some efforts have also been dedicated to improve the prediction of missing data, based on correctly received ones (see, e.g., [14, 22] for details).
Even if the error resilience and error concealment techniques have become very effective, it is still impossible to solve completely the problem of temporal prediction drift: error concealment is clearly unable to properly compensate for channel losses. In these cases, because of the dependencies introduced by a prediction loop, reconstruction errors in a single frame can propagate across the group of picture (GOP) in the decoded video, leading to serious impairments in the overall quality.
As already mentioned in the previous sections, besides the more traditional approaches discussed above, a new error resilient coding strategy has emerged. This new scheme, which has been proposed, for example, in [23–25] and further developed and improved in [4, 5, 26–28] relies on the principles of DVC. The basic idea underlying this scheme is the following: an auxiliary stream is sent in parallel to the main stream as a redundant representation of the video sequence, and it is used to correct errors at the decoder, using the traditionally transmitted video stream (possibly corrupted) as side information.
This approach exploits the main feature of DVC, that is, at the encoder no knowledge of the side information is required. This is a key point, since it is not known a priori which packets will be lost during the transmission. In DVC, the channel noise can be modelled as an increase in the correlation noise between the side information and the signal that needs to be reconstructed. This feature is the main reason for which distributed source coding is believed to have an intrinsic resilience to transmission errors. The properties of DVC in terms of error resilience have been discussed, for example, in [6, 7, 16]. Nevertheless, an accurate analysis of the behavior of the two basic architectures of distributed video codecs has only been preliminary conducted. In the following, a more in-depth evaluation of the error robustness for DVC schemes will be provided.
4. Distributed Video Coding Architectures
Let us first describe the architectures of the two main, distributed video coding schemes, namely an interpolation based distributed codec, as proposed by Stanford a few years ago [8–10] and further developed within the DISCOVER European funded project [13], and a backward prediction-based distributed codec (PRISM, [11, 12]).
4.1. Interpolation-Based Distributed Video Coding
In Figure 3, the block diagram of such a codec as proposed by Girod et al. is drawn. No detailed description for every single block of the codec will be given (interested readers may refer to [8, 10, 13, 29] for a more accurate presentation of each component).
The encoder works independently on each video frame, performing thus a so-called intra coding of the frames. The even indexed frames, that are referred to as key-frames (KF), are traditionally encoded using, for example, an H.264/AVC encoder operating in intra mode (i.e., without using any inter-frame prediction). The odd indexed frames instead, called Wyner-Ziv (WZ) frames, are encoded using the principles of distributed source coding. More specifically, these frames are first transformed, with a block based DCT, and then quantized thanks to proper quantization matrices. Homologous coefficients are then encoded, bit plane by bit plane, using a suitable turbo code. In particular, each bit plane of each frequency band is fed into a turbo encoder with rate  ; while information bits are discarded, parity bits are properly stored in a buffer. The encoded bit stream is thus composed of two different parts: the H.264/AVC intra coded key-frame stream, and the WZ stream. The key-frame information is entirely sent to the decoder, while the parity bits are only partially sent, depending on the decoder requests to the encoder, provided iteratively through a feedback channel.
; while information bits are discarded, parity bits are properly stored in a buffer. The encoded bit stream is thus composed of two different parts: the H.264/AVC intra coded key-frame stream, and the WZ stream. The key-frame information is entirely sent to the decoder, while the parity bits are only partially sent, depending on the decoder requests to the encoder, provided iteratively through a feedback channel.
At first the key-frames are decoded from the traditional encoded stream. Then, the decoding of a WZ frame is performed by first generating a side information (SI), that is an estimate of the missing frame, usually obtained by motion compensated interpolation between two adjacent previously decoded key-frames. This estimate is used to extract a first rough approximation of the information bits of the original quantized frame. These bits are then corrected at best by means of a turbo decoding process that uses the parity bits received from the encoder.
As mentioned the parity bits are not sent all at once, but they are iteratively requested by the decoder, through a feedback channel, until the estimated error probability on the decoded bit plane reaches a predefined threshold. In this way, the decoder usually achieves the desired quality during the decoding phase, and the performance of the encoding scheme is mainly reflected in the total rate sent by the encoder in order to achieve that quality. This fact is important as far as the problem of error resilience is concerned, since it will be partially responsible for the rate/quality trade-off.
It has to be noted that an appropriate packetization strategy of the WZ bits must be adopted to ensure a reasonable trade-off between packet header and associated payload. One such strategy consists in grouping the WZ bits of a puncturing step associated to all the coefficients of a same bit plane in a single packet. For example, when transmitting a QCIF sequence, one bit plane of a single band contains roughly 3200 bits, which means that for every puncturing there are about 100 bits. This would actually be a very small payload to be sent in a single packet. By grouping puncturing bits of a same bit plane for different coefficients, however, one can send roughly 200 bytes per packet, which becomes a reasonable payload size.
4.2. Backward Prediction-Based Distributed Video Coding (PRISM)
In Figure 4, the PRISM codec block diagram is shown. We briefly introduce this architecture and refer the reader to [11, 12, 16, 30] for a more detailed presentation.
The whole PRISM system is based on a block wise approach. The first frame (named key-frame) of a (GOP) is encoded in a conventional intra frame way (e.g., JPEG). The remaining frames in the GOP are encoded in a Wyner-Ziv fashion, as briefly described in the next paragraphs.
At first, each block of a WZ frame is classified into one of  categories, namely, SKIP, INTRA, or INTER. Then, each block undergoes a proper encoding-decoding process, as follows.
categories, namely, SKIP, INTRA, or INTER. Then, each block undergoes a proper encoding-decoding process, as follows.
-
(i)
SKIP blocks are not processed; at the decoder side, each SKIP block is simply replaced with the co located block extracted from the previous frame.
-
(ii)
INTRA blocks are intra frame encoded using the run-amplitude source coding of a JPEG-like encoder, the very same used to code the key-frames; in this way, the decoding process does not need further information to recover an INTRA block.
-
(iii)
INTER blocks are
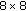 DCT transformed; the low-frequency DCT coefficients are then properly quantized, and parity bits are calculated on the two least significant bits of the quantization indices. A cyclic redundancy check (CRC) is also computed for each block of the low-frequency coefficients and transmitted separately. Higher-frequency DCT coefficients are entropy encoded with a classic run-amplitude code, and, possibly, some uncorrelated refinement bits for the low-frequency coefficients are added to the stream to achieve higher reconstruction quality.
DCT transformed; the low-frequency DCT coefficients are then properly quantized, and parity bits are calculated on the two least significant bits of the quantization indices. A cyclic redundancy check (CRC) is also computed for each block of the low-frequency coefficients and transmitted separately. Higher-frequency DCT coefficients are entropy encoded with a classic run-amplitude code, and, possibly, some uncorrelated refinement bits for the low-frequency coefficients are added to the stream to achieve higher reconstruction quality.
The decoder recovers at first the SKIP and INTRA blocks, and then performs WZ decoding of the INTER blocks, using the procedure described in the next paragraphs.
For each WZ block, a set of potential motion compensated predictors (SI) is formed from all the blocks extracted from a window centered around the co located block in the previous frame. For every candidate predictor, a WZ decoding is performed using the received parity bits of the original transformed coefficients. The associated CRC is computed on the resulting decoded block. If the CRC matches with that received from the encoder, then the WZ block is flagged as successfully decoded, and the process is repeated on the next WZ block. If instead the CRC does not match, another candidate predictor is considered, until all possible predictors have been tested. A decoding failure is declared when no candidate predictor lead to a successfull CRC. In this case, since no reliable predictor is available for the current block, a zero-motion concealment is performed on such block. Since the PRISM codec does not use any feedback channel, decoding failure is more frequent when the channel is error prone, which lead to a PSNR impairment, while the rate is unaltered with respect to the error-free case. In some sense it is possible to say that this decoding process performs a joint motion estimation and WZ decoding. It is important to note that the correctness of the estimated motion is by no means important, the only important result being a correct CRC (which presumably implies a correct reconstruction of the original DCT coefficients).
After successful WZ decoding of the low-frequency coefficients, the high-frequency coefficients and the refinement bits are decoded to completely recover the quantized transformed representation, which is finally inverted to obtain the decoded frame.
5. Error Resilience Performance Evaluation
To evaluate the error resilience capabilities of DVC, the two distributed video coding architectures previously described have been analyzed and compared. The codec based on the Stanford approach was implemented following the architecture proposed in [8] and further developed within the European funded project DISCOVER (DISCOVER software was developed from the IST_WZ software developed at the Image Group of the Instituto Superior Técnico (IST) of Lisbon by Catarina Brites, João Ascenso, and Fernando Pereira.) (see, [13]; for convenience, this codec will be referred to as DISCOVER codec from now onward). Considering the PRISM codec, we have used an implementation derived from the system described in principle in [11] and in more detail in [30].
The simulation results will be discussed following the guidelines described below.
-
(i)
Frame-by-frame temporal analysis in presence of channel errors. To better understand the effects of transmission errors we have first analyzed the frame-by-frame PSNR at a given bit rate, so as to analyze the temporal behavior of each codec, and so as to understand their strength in terms of error resilience. The results of these simulations are described in Section 5.1.
-
(ii)
Rate/distortion analysis in presence of channel errors. In these experiments, we have computed and compared the rate/distortion curves, in the case no error protection is performed. Specifically we are reporting the results obtained for the DISCOVER codec, the PRISM codec and one configuration of H.264/AVC, with GOP2 in IBIB mode. The results of these simulations are described in Section 5.2.
-
(iii)
Rate/distortion in presence of channel errors and FEC protection. In order to evaluate the error propagation in the traditional predictive coding, we have compared the PSNR curves obtained with the DISCOVER codec with those obtained with H.264/AVC GOP8, with the introduction of a FEC protection. The results of these simulations are described in Section 5.3.
Before discussing the results, we provide the general setup of the simulation and describe the conditions that have been kept constant throughout all experiments. Specific details will be provided prior to the discussion of the results of each run of simulations. The video sequences used in all the simulations are in QCIF format, at  frames-per-second. The encoded bitstreams have been transmitted over a packet network affected by a given packet loss rate (PLR). This is considered a realistic scenario according to modern telecommunication network characteristics. The packet loss patterns have been generated using a uniform random distribution; of course a packet loss has different effects, depending on the type of the lost data.
frames-per-second. The encoded bitstreams have been transmitted over a packet network affected by a given packet loss rate (PLR). This is considered a realistic scenario according to modern telecommunication network characteristics. The packet loss patterns have been generated using a uniform random distribution; of course a packet loss has different effects, depending on the type of the lost data.
As a general comment, let us note that the considered architectures exhibit substantial differences, and any comparison is therefore necessarily affected by some sort of unfairness. For example the DISCOVER architecture requires a feedback channel, while PRISM is designed to work in absence of any feedback from the decoder; the encoded data types and therefore their packetization strategies are different; also the concealment strategies cannot be the same for both codecs. Nevertheless, we present jointly performed tests for the considered codecs, in order to help evaluating the pro and cons of each architecture in terms of robustness to channel errors.
5.1. Frame-by-Frame Temporal Analysis
5.1.1. DISCOVER Codec Temporal Performance Assessment
In this section we present a temporal evaluation of the behavior of the DISCOVER codec in the presence of transmission errors.
Experimental Setup
In these experiments we have simulated the transmission in the general conditions previously described. The DISCOVER codec has been configured to work with GOP2 size.
We have assumed that any lost packet containing WZ bits will be requested again through the feedback channel, so that the loss of a WZ packet will leads only to an increase in the bitrate, without affecting the reconstructed frame quality. Since the key-frames are H.264/AVC encoded, we have exploited the H.264/AVC standard packetization features.
In particular, each frame has been divided into slices containing up to 200 bytes. Zero padding was imposed to reach the 200 bytes size for smaller size slices. Each slice is assumed to represent the payload of a single network packet. We have also enabled the flexible macroblock ordering (FMO) feature, in dispersed mode; in this way each slice is composed of non adjacent macroblocks.
Lost slices in the key-frames have been concealed using the standard intra frame concealment strategy used in H.264/AVC JM11 decoder, whereas no concealment has been applied to the WZ frames. We have assumed also that header and motion information contained in the H.264/AVC stream is properly protected, so that the high level information about slices positions and type is always correctly received. Also in this case, the PSNR plots have been obtained by averaging the performance of 20 experimental simulations with a different error pattern realization.
Simulation Results
We have first considered the frame-by-frame PSNR fluctuations, in order to evaluate the temporal effects of channel errors.
In Figure 5, the results obtained with the DISCOVER codec are reported. In this case, we can see that the frame-by-frame PSNR curve shows significant oscillations. In particular, there is a clear difference between the behavior of the key-frames and the behavior of the Wyner-Ziv frames. While some of the key-frames (odd indexed) are strongly corrupted by noise, the quality of the WZ frames (even indexed ones) is always close to the error-free case, also when the side information is generated from bad quality corrupted key-frames.
To better understand this behavior, we have analyzed these curves jointly with those plotted in Figure 6, representing the associated frame-by-frame bitrate. We can notice that the WZ frames that are reconstructed on the basis of the corrupted side information require a higher bitrate than they would need in case no transmission errors had occurred. This proves that the decoder can react effectively to a bad quality side information by asking more parity bits to the encoder. Indeed, the quality of the decoded WZ frames is much higher than that of the corrupted key-frames.
However the resulting oscillating pattern in decoded quality appears perceptually very objectionable. This should be taken into account when assessing the benefit of a more robust average R(D) performance with respect to more constant quality behavior.
In Figures 7 and 8, similar results can be observed for the Hallmonitor test sequence.
The results of our simulations highlight that the DISCOVER architecture is strongly affected by the errors concealment strategy used for H.264/AVC. Indeed, the key-frames are H.264/AVC encoded and therefore packet losses lead to quality impairments which depend on the concealment strategy and on the other H.264/AVC resilience tools that are employed. The WZ frames are encoded in a purely distributed fashion. As a consequence, the quality of the reconstructed WZ frames is in general very close to the quality obtained in the error-free case, even if the key-frames quality strongly influences the derived side information.
The increase in the WZ rate is mainly due to two causes. On the one hand, lost packets need to be retransmitted. On the other hand, quality impairments in the key-frames, due to slice losses, lead to worse side information, so that more parity bits are necessary for the correction.
From these simulations, it emerges that the main drawback of the DISCOVER approach (based on the feedback channel) in terms of error resilience seems to be the lack of uniformity in the behavior of the two components of the bit stream. In fact, packet losses could be quite annoying in terms of visual quality in the key-frames, while WZ frames are characterized by higher quality. The drift problem is easily circumvented since in general the WZ frames compensate for the side information loss.
In Figures 9(a), 9(b), and 9(c), an example of visual quality is reported. Figures 9(a) and 9(c) correspond to frame n.23 and frame n.25, respectively, and they are key-frames, while their interleaving WZ frame (frame n.24) is reported in Figure 9(b). During the transmission of the first one (corresponding to frame n.23 in the plots of Figures 5 and 6) a slice loss has occurred, leading to a very significant quality impairment. On the contrary, the following key-frame (Figure 9(c), frame 25 in the plots of Figures 5 and 6) has been correctly received. The WZ frame initially predicted from these key-frames is characterized after decoding by a high PSNR and good visual quality, as can be observed in Figure 9(b).
Since the previously discussed results highlight that there is a strong difference in the behavior of the two components of the DISCOVER encoded bitstream, we report separately their respective rate-distortion plots. In Figure 10, the rate-distortion plot, for a packet loss rate of  , is shown for the WZ frames of the Foreman sequence. At low bit rates the performance loss is about 1 dB. The plot in Figure 11, shows that the PSNR loss of the corrupted key-frames is lower at high bitrates than at low bitrates. The results confirm that the feedback requests to the encoder can compensate relatively well the initial low quality side information. In Figures 12 and 13 similar results are obtained for the Hallmonitor sequence.
, is shown for the WZ frames of the Foreman sequence. At low bit rates the performance loss is about 1 dB. The plot in Figure 11, shows that the PSNR loss of the corrupted key-frames is lower at high bitrates than at low bitrates. The results confirm that the feedback requests to the encoder can compensate relatively well the initial low quality side information. In Figures 12 and 13 similar results are obtained for the Hallmonitor sequence.
5.1.2. PRISM Codec Temporal Performance Assessment
In this section we report and discuss the results of the simulations of PRISM codec, in order to understand its sensitivity to transmission errors and its error resilience properties.
Experimental Setup
In the PRISM codec evaluation we have again analyzed the frame-by-frame PSNR fluctuations. The encoded bitstream has been transmitted over a packet network, affected by a given PLR. In the case of PRISM, instead of applying to the stream a FMO or a packetization in sequential order, we have assumed that encoded blocks are scrambled so that the probability of losing a block corresponds to the PLR.
As we did in the case of DISCOVER, we have assumed that the header containing the block type maps is correctly received, so that the decoder always knows the class a block belongs to.
In order to roughly compensate for packet losses, a simple concealment strategy has been adopted. Lost blocks are replaced by the co located blocks in the previous frame (zero-motion prediction).
Moreover, we have analyzed the role of the distributed component of the scheme, that is, the Wyner-Ziv blocks. Specifically, we have transmitted only the INTRA blocks, and we have concealed the WZ blocks using the same concealment technique used for the lost blocks. In this way we can evaluate the relative contribution given by the transmitted WZ bits, with respect to the bits associated to the other block types.
Simulation Results
The results obtained with the PRISM codec are shown in Figures 14 and 15, for a packet loss rate of  , and, as a reference, for an error-free transmission (Foreman and Hallmonitor sequences, resp.). It can be observed that the PSNR degradation is substantially uniform through the various frames. Local PSNR losses are due to errors in the decoder-side motion estimation, and are therefore present also in the error-free curve. In the PRISM codec, the visual quality is more uniform than in DISCOVER, because every frame is encoded combining traditional and WZ encoding, in a block wise fashion. This uniformity in the perceived quality carries as a drawback an increased sensitivity to the drift problem with respect to the DISCOVER architecture. Moreover, even if the PRISM quality is uniform through time, the presence of few very low quality blocks in the decoded frames can be annoying.
, and, as a reference, for an error-free transmission (Foreman and Hallmonitor sequences, resp.). It can be observed that the PSNR degradation is substantially uniform through the various frames. Local PSNR losses are due to errors in the decoder-side motion estimation, and are therefore present also in the error-free curve. In the PRISM codec, the visual quality is more uniform than in DISCOVER, because every frame is encoded combining traditional and WZ encoding, in a block wise fashion. This uniformity in the perceived quality carries as a drawback an increased sensitivity to the drift problem with respect to the DISCOVER architecture. Moreover, even if the PRISM quality is uniform through time, the presence of few very low quality blocks in the decoded frames can be annoying.
In these figures it is also reported the frame-by-frame PSNR in case of no transmission of the WZ blocks. It can be observed that, in case of transmission of the WZ blocks, the PSNR is in general higher, showing that the WZ bits can help the compensation of the channel losses. The same behavior can be observed, in a more global context, in the PSNR curves reported in Figure 16, for the Foreman sequence. Also in this case, it can be seen that at high bit rates the WZ information is important in order to help the compensation of the channel losses.
A different behavior can be observed in the case of the Hallmonitor sequence (Figure 17). For this sequence it is always convenient (at least in terms of average PSNR) not to send the WZ information. In fact, when the WZ parity bits are not transmitted, each working point has not only lower PSNR but also lower rate, so the No WZ curve is over the standard PRISM one. This is due to the fact that the PRISM behavior heavily depends on the motion content of the sequence.
To give a more complete picture of this behavior, we have also reported the simulation results obtained with other sequences, namely Flowergarden (Figure 18), Coastguard (Figure 19), Soccer (Figure 20).
5.2. Comparison of the Considered Architectures in Terms of Rate/Distortion
In this section the DISCOVER and PRISM architectures are compared to H.264/AVC, GOP2 IBIB mode, in case of transmission over a network with packet losses.
Experimental Setup
The DISCOVER and PRISM experimental setups are the same considered for their respective frame-by-frame analysis. For H.264/AVC we have used the same setup of the DISCOVER key-frames. Each slice has been transmitted in a single packet, using FMO and intra frame concealment. H.264/AVC is working in GOP2 IBIB mode. The PSNR has been evaluated and averaged considering  different error patterns.
different error patterns.
Simulation Results
Figures 21, 22, 23, 24, 25, 26, 27, 28, 29, and 30 show the PSNR curves obtained for the considered test sequences (namely, Coastguard, Flowergarden, Foreman, Hallmonitor, Soccer), at a PLR of  ,
,  and
and  .
.
It can be observed that in all cases, except in Hallmonitor, the DISCOVER codec outperforms PRISM, both in terms of PSNR in the error-free case, and in terms of quality loss in presence of channel errors.
We can see that PSNR loss due to transmission errors for the DISCOVER codec ranges from about 0.5 dB at low bitrates to more than 3 dB at high bitrates, depending on the considered video sequence. This loss is mainly due to the impairment in the key-frames, since, as described in Section 5.1.1, the WZ frames quality is very close to the corresponding error-free one.
The quality impairments in PRISM are substantially similar, even if the overall average quality is in general worse.
From all the reported results, a strong dependence of the performance, in terms of both compression and error resilience, on the content of the test sequence, comes out. In particular, PRISM seems to perform quite well in low motion sequences, so it could be well suited, for example, for video surveillance applications.
Compared to H.264/AVC, the DISCOVER codec tends to lead to slight superior PSNR performance as the PLR increases. This is due to the fact that the H.264/AVC is not able to compensate for lost information, whereas the DVC codec is able to request additional parity bits through the feedback channel. Clearly this communication diversity may not be considered completely fair for the comparison. Moreover, it is important to note that this average quality increase would not be reflected in terms of a perceptual quality increase. Indeed key-frame quality would remain poor, whereas WZ frames can be well reproduced, which cannot be perceptually well tolerated.
H.264/AVC comparison with respect to PRISM is two-fold. For sequences exhibiting limited motion (e.g., Hallmonitor), PRISM can better compensate for information loss, whereas it cannot compete for sequences exhibiting complex motion patterns. The main reason may be due to the lower coding efficiency of current PRISM implementations when compared to H.264/AVC when there are no transmission errors.
5.3. DISCOVER versus H.264/AVC Performance Assessment (FEC Protection)
In order to evaluate the error propagation in DVC and in the traditional predictive coding systems, in this section we have compared the PSNR curves obtained with the DISCOVER codec with those obtained with H.264/AVC GOP8, with the introduction of a simple FEC protection.
Experimental Setup
The tests presented in this section have been performed under the same conditions described in the beginning of Section 5; the DISCOVER codec is set to GOP2 mode, with FMO and intra frame concealment on the key-frames, without any concealment on WZ frames.
For H.264/AVC the same setup of the DISCOVER key-frames has been adopted. Each slice has been transmitted in a single packet, using FMO and intra frame concealment. H.264/AVC is constrained to work in GOP8 IPP mode.
In order to perform a simple protection of the encoded data, we have introduced a basic FEC protection both on the DISCOVER key-frame stream, and on the H.264/AVC stream. This protection has been performed according to the scheme described in [4] (see Figure 31). An  Reed-Solomon code (in our case, a
Reed-Solomon code (in our case, a  code) has been applied across a group of
code) has been applied across a group of  slices, to obtain
slices, to obtain  groups of parity bytes. Each group of parity symbols is supposed to be sent as a different packet. As a
groups of parity bytes. Each group of parity symbols is supposed to be sent as a different packet. As a  Reed-Solomon code can correct up to
Reed-Solomon code can correct up to  erasures, with this scheme the loss of at most
erasures, with this scheme the loss of at most  packets can be compensated for. The rate of the considered Reed-Solomon code is
packets can be compensated for. The rate of the considered Reed-Solomon code is  . The WZ part of the encoded bitstream is supposed to be sent unprotected, since in most cases additional parity bits are sufficient to achieve proper decoding.
. The WZ part of the encoded bitstream is supposed to be sent unprotected, since in most cases additional parity bits are sufficient to achieve proper decoding.
Performance Comparison
We have repeated the simulation at different coding rates using the described configurations. Figures 32, 33, 34, 35, 36, 37, 38, 39, 40, and 41 report the obtained PSNR curves for a PLR of  ,
,  , and
, and  .
.
We can notice that, for the considered values of PLR and with this FEC protection, H.264/AVC gives better performance than DISCOVER until a PLR of  .
.
Considering a PLR of  , DISCOVER outperforms slightly H.264/AVC, and the performance gain increases with the bitrate. Moreover, the H.264/AVC quality increases very slowly, due to the fact that the number of lost slices is often higher than the correcting capability of the channel code. On the contrary, the quality obtained with the distributed codec still increases in all the considered cases.
, DISCOVER outperforms slightly H.264/AVC, and the performance gain increases with the bitrate. Moreover, the H.264/AVC quality increases very slowly, due to the fact that the number of lost slices is often higher than the correcting capability of the channel code. On the contrary, the quality obtained with the distributed codec still increases in all the considered cases.
Clearly, if we assume that also the H.264 codec was provided with a feedback channel, there would be the possibility to use a rateless FEC code with feedback. In this case, the H.264+FEC system would be able to compensate for transmission errors in a similar manner to a DVC solution that uses feedback; the FEC decoder would simply keep requesting rateless FEC packets until it could decode the received data successfully. It is likely that the H.264 codec would be much better performing in this case given the margin it has with respect to the DVC-based solution in the error-free case.
6. Conclusions
In this paper, the error resilience properties of DISCOVER and PRISM distributed video coding architectures have been compared in presence of transmission errors over packet networks. Specifically, an accurate temporal and rate/distortion based evaluation of the effects of the errors for both the considered DVC architectures has been performed and discussed. Both the Stanford approach and the PRISM approach have been compared with H.264/AVC. For the PRISM approach, only the case of transmission without error protection has been considered. On the contrary, the comparison between the Stanford approach and H.264/AVC has been carried out in both cases of no error protection and simple FEC error protection.
The frame-by-frame PSNR plots demonstrate the ability, at least in principle, of DVC architectures to be error resilient. The simulation results highlight that the DISCOVER codec can react positively to the presence of low quality side information asking more WZ bits to the encoder, leading to a WZ frames quality very close to the error-free case. The key-frames quality is in general lower, since it strongly depends on H.264/AVC error resilience and concealment tools. In this respect, it is very important to note that this average quality increase would not be reflected in terms of a perceptual quality increase. Indeed key-frames quality would remain poor, whereas WZ frames can be well reproduced, which cannot be perceptually well tolerated. The quality of the PRISM reconstructed sequences is on the other hand more uniform across frames; nevertheless the presence of few very low quality blocks inside each frame impairs the overall perceived quality. The uniformity in the perceived temporal quality carries as a drawback a slight increased sensitivity to the drift problem.
Compared to H.264/AVC GOP2, the DISCOVER codec tends to lead to better PSNR performance as the PLR increases. This is due to the fact that the H.264/AVC is not able to compensate for lost information, whereas the DVC codec is able to request additional parity bits through the feedback channel. Clearly this communication diversity may not be considered completely fair for the comparison. H.264/AVC GOP2 comparison with respect to PRISM shows that, for sequences exhibiting limited motion (e.g., Hallmonitor), PRISM can better compensate for information loss, whereas it cannot compete for sequences exhibiting more complex motion patterns.
In order to better evaluate the effects of error propagation in DVC and in the traditional predictive coding systems, we have also compared the PSNR curves obtained with the DISCOVER codec with those obtained with H.264/AVC GOP8, with the introduction of a simple FEC protection. From the simulation results, we can notice that, with the considered settings, H.264/AVC gives better performance than DISCOVER until a PLR of  . Considering PLR of
. Considering PLR of  , DISCOVER outperforms slightly H.264/AVC, and the performance gain slowly increases with the bitrate.
, DISCOVER outperforms slightly H.264/AVC, and the performance gain slowly increases with the bitrate.
As a general comment, the obtained results highlight that in all the considered cases there is a strong dependence of the behavior of the various codecs on the content of the considered video sequence. In particular, PRISM seems to be particularly well suited for low motion sequences, whereas DISCOVER gives better results in the other cases.
It has also to be mentioned that, in general, it is quite difficult to perform a fair comparison in terms of rate-distortion between the considered architectures, because of their several strong structural differences.
We have chosen to use H.264/AVC as a reference because it represents the state of art in traditional coding, and we have chosen to use it in a scenario exhibiting the most common features. This is the reason why we accept some unfairness in the comparison, in the sense that a feedback channel is given to the WZ part of the distributed codec. We also remark that the WZ feedback requires very few bits: in fact it just signals whether new WZ bits are required or not. Nevertheless, if H.264/AVC is given a feedback channel, it can reach very satisfactory performance.
References
Guillemot C, Pereira F, Torres L, Ebrahimi T, Leonardi R, Ostermann J: Distributed monoview and multiview video coding. IEEE Signal Processing Magazine 2007,24(5):67-76.
Slepian D, Wolf JK: Noiseless coding of correlated information sources. IEEE Transactions on Information Theory 1973,19(4):471-480. 10.1109/TIT.1973.1055037
Wyner AD, Ziv J: The rate-distortion function for source coding with side information at the decoder. IEEE Transactions on Information Theory 1976,22(1):1-10. 10.1109/TIT.1976.1055508
Baccichet P, Rane S, Girod B: Systematic lossy error protection based on H.264/AVC redundant slices and flexible macroblock ordering. Proceedings of Packet Video Workshop (PV '06), April 2006, Hangzhou, China
Rane S, Baccichet P, Girod B: Modeling and optimization of a systematic lossy error protection system based on H.264/AVC redundant slices. Proceedings of the 25th International Picture Coding Symposium (PCS '06), April 2006, Beijing, China
Tonoli C, Dalai M, Migliorati P, Leonardi R: Error resilience performance evaluation of a distributed video codec. Proceedings of the International Picture Coding Symposium (PCS '07), November 2007, Lisbon, Portugal
Pedro JQ, Soares LD, Brites C, et al.: Studying error resilience performance for a feedback channel based transform domain Wyner-Ziv video codec. Proceedings of the International Picture Coding Symposium (PCS '07), November 2007, Lisbon, Portugal
Aaron A, Zhang R, Girod B: Wyner-Ziv coding for motion video. Proceedings of the 36th Asilomar Conference on Signals, Systems and Computers, November 2002, Pacific Grove, Calif, USA
Aaron A, Rane SD, Setton E, Girod B: Transform-domain Wyner-Ziv codec for video. Visual Communications and Image Processing, January 2004, San Jose, Calif ,USA, Proceedings of SPIE 5308: 520-528.
Girod B, Aaron AM, Rane S, Rebollo-Monedero D: Distributed video coding. Proceedings of the IEEE 2005,93(1):71-83.
Puri R, Ramchandran K: PRISM: a new robust video coding architecture based on distributed compression principles. Proceedings of the 40th Allerton Conference on Communication, Control and Computing, October 2002, Allerton, Ill, USA
Puri R, Ramchandran K: PRISM: a new "reversed" multimedia coding paradigm. Proceedings of International Conference on Image Processing (ICIP '03), September 2003, Barcelona, Spain 1: 617-620.
Artigas X, Ascenso J, Dalai M, Klomp S, Kubasov D, Ouaret M: The DISCOVER codec: architecture, techniques and evaluation. Proceedings of the International Picture Coding Symposium (PCS '07), November 2007, Lisbon, Portugal 6: 14496-14410.
Wiegand T, Sullivan GJ, Bjøntegaard G, Luthra A: Overview of the H.264/AVC video coding standard. IEEE Transactions on Circuits and Systems for Video Technology 2003,13(7):560-576.
Pradhan SS, Ramchandran K: Distributed source coding using syndromes (DISCUS): design and construction. IEEE Transactions on Information Theory 2003,49(3):626-643. 10.1109/TIT.2002.808103
Puri R, Majumdar A, Ramchandran K: PRISM: a video coding paradigm with motion estimation at the decoder. IEEE Transactions on Image Processing 2007,16(10):2436-2448.
Wang Y, Zhu Q-F: Error control and concealment for video communication: a review. Proceedings of the IEEE 1998,86(5):974-997. 10.1109/5.664283
Kim J, Mersereau RM, Altunbasak Y: Error-resilient image and video transmission over the internet using unequal error protection. IEEE Transactions on Image Processing 2003,12(2):121-131. 10.1109/TIP.2003.809006
Huang C-L, Liang S: Unequal error protection for MPEG-2 video transmission over wireless channels. Signal Processing: Image Communication 2004,19(1):67-79. 10.1016/j.image.2003.08.018
Wang Y, Yu S, Yang X: Unequal error protection for robust wireless transmission using LDPC codes. Proceedings of the 25th International Picture Coding Symposium (PCS '06), April 2006, Beijing, China
Poulliat C, Declercq D, Fijalkow I: Enhancement of unequal error protection properties of LDPC codes. EURASIP Journal on Wireless Communications and Networking 2007, Article ID 92659, 2007:-9.
Kumar S, Xu L, Mandal MK, Panchanathan S: Error resiliency schemes in H.264/AVC standard. Journal of Visual Communication and Image Representation 2006,17(2):425-450. 10.1016/j.jvcir.2005.04.006
Aaron A, Rane S, Zhang R, Girod B: Wyner-Ziv coding for video: applications to compression and error resilience. Proceedings of IEEE Data Compression Conference (DCC '03), March 2003, Snowbird, Utah, USA 93-102.
Aaron A, Rane S, Rebollo-Monedero D, Girod B: Systematic lossy forward error protection for video waveforms. Proceedings of the International Conference on Image Processing (ICIP '03), September 2003, Barcelona, Spain 1: 609-612.
Sehgal A, Jagmohan A, Ahuja N: Wyner-Ziv coding of video: an error-resilient compression framework. IEEE Transactions on Multimedia 2004,6(2):249-258. 10.1109/TMM.2003.822995
Wang J, Majumdar A, Ramchandran K, Garudadri H: Robust video transmission over a lossy network using a distributed source coded auxiliary channel. Proceedings of the International Picture Coding Symposium (PCS '04), December 2004, San Francisco, Calif, USA 41-46.
Fumagalli M, Tagliasacchi M, Tubaro S: Improved bit allocation in an error-resilient scheme based on distributed source coding. Proceedings of IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP '06), May 2006, Toulouse, France 2: 61-64.
Rane S, Aaron A, Girod B: Error-resilient video transmission using multiple embedded Wyner-Ziv descriptions. Proceedings of International Conference on Image Processing (ICIP '05), September 2005, Genoa, Italy 2: 666-669.
Brites C, Ascenso J, Pereira F: Improving transform domain Wyner-Ziv video coding performance. Proceedings of IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP '06), May 2006, Toulouse, France 2: 525-528.
Fowler JE: An implementation of PRISM using QccPack. Tech. Rep. MSSU-COE-ERC-05-01 Mississippi State ERC, Mississippi State University, Mississippi State, Miss, USA; January 2005.
Acknowledgments
The work presented in this paper was partially developed within DISCOVER (Distributed Coding for Video Services), a European Commission funded Future and Emerging Technologies (FET) project (http://www.discoverdvc.org/). DISCOVER software started from the IST_WZ software developed at the Image Group of the Instituto Superior Técnico (IST) of Lisbon by Catarina Brites, João Ascenso, and Fernando Pereira.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License ( https://creativecommons.org/licenses/by/2.0 ), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Tonoli, C., Migliorati, P. & Leonardi, R. Error Resilience in Current Distributed Video Coding Architectures. J Image Video Proc 2009, 946585 (2009). https://doi.org/10.1155/2009/946585
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1155/2009/946585




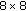 DCT transformed; the low-frequency DCT coefficients are then properly quantized, and parity bits are calculated on the two least significant bits of the quantization indices. A cyclic redundancy check (CRC) is also computed for each block of the low-frequency coefficients and transmitted separately. Higher-frequency DCT coefficients are entropy encoded with a classic run-amplitude code, and, possibly, some uncorrelated refinement bits for the low-frequency coefficients are added to the stream to achieve higher reconstruction quality.
DCT transformed; the low-frequency DCT coefficients are then properly quantized, and parity bits are calculated on the two least significant bits of the quantization indices. A cyclic redundancy check (CRC) is also computed for each block of the low-frequency coefficients and transmitted separately. Higher-frequency DCT coefficients are entropy encoded with a classic run-amplitude code, and, possibly, some uncorrelated refinement bits for the low-frequency coefficients are added to the stream to achieve higher reconstruction quality.



































