- Research Article
- Open access
- Published:
Optical Music Recognition for Scores Written in White Mensural Notation
EURASIP Journal on Image and Video Processing volume 2009, Article number: 843401 (2009)
Abstract
An Optical Music Recognition (OMR) system especially adapted for handwritten musical scores of the XVII-th and the early XVIII-th centuries written in white mensural notation is presented. The system performs a complete sequence of analysis stages: the input is the RGB image of the score to be analyzed and, after a preprocessing that returns a black and white image with corrected rotation, the staves are processed to return a score without staff lines; then, a music symbol processing stage isolates the music symbols contained in the score and, finally, the classification process starts to obtain the transcription in a suitable electronic format so that it can be stored or played. This work will help to preserve our cultural heritage keeping the musical information of the scores in a digital format that also gives the possibility to perform and distribute the original music contained in those scores.
1. Introduction
Optical Music Recognition (OMR) aims to provide a computer with the necessary processing capabilities to convert a scanned score into an electronic format and even recognize and understand the contents of the score. OMR is related to Optical Character Recognition (OCR); however, it shows several differences based on the typology of the symbols to be recognized and the structure of the framework [1]. OMR has been an active research area since the 70s but it is in the early 90s when the first works for handwritten formats [2] and ancient music started to be developed [3, 4]. Some of the most recent works on ancient music recognition are due to Pugin et al. [5], based on the implementation of hidden Markov models and adaptive binarization, and to Caldas Pinto et al. [6], with the development of the project ROMA (Reconhecimento Óptico de Música Antiga) for the recognition and restoration of ancient music manuscripts, directed by the Biblioteca Geral da Universidade de Coimbra.
Of course, a special category of OMR systems deal with ancient handwritten music scores. OMR applied to ancient music shows several additional difficulties with respect to classic OMR [6]. The notation can vary from one author to another or among different scores of the same artist or even within the same score. The size, shape, and intensity of the symbols can change due to the imperfections of handwriting. In case of later additional interventions on the scores, other classes of symbols, often with different styles, may appear superimposed to the original ones. The thickness of the staff lines is not a constant parameter anymore and the staff lines are not continuous straight lines in real scores. Moreover, the original scores get degraded by the effect of age. Finally, the digitized scores may present additional imperfections: geometrical distortions, rotations, or even heterogeneous illumination.
A good review of the stages related to the OMR process can be found in [7] or [8]. These stages can be described as follows: correction of the rotation of the image, detection and processing of staff lines, detection and labeling of musical objects, and recognition and generation of the electronic descriptive document.
Working with early scores makes us pay a bit more attention to the stages related to image preprocessing, to include specific tasks devoted to obtain good binary images. This topic will also be considered in the paper together with all the stages required and the specific algorithms developed to get an electronic description of the music in the scores.
The OMR system described in this work is applied to the processing of handwritten scores preserved in the Archivo de la Catedral de Málaga (ACM). The ACM was created at the end of the XV-th century and it contains music scores from the XV-th to the XX-th centuries. The OMR system developed will be evaluated on scores written in white mensural notation. We will distinguish between two different styles of notation: the style mainly used in the scores by Stephano di Britto and the style mainly used by Francisco Sanz (XVII-th century and early XVIII-th century, resp.). So, the target scores are documents written in rather different styles (Figure 1): Britto (Figure 1(a)) uses a rigorous style, with squared notes. Sanz (Figure 1(b)) shows a handwritten style close to the modern one, with rounded notes and vertical stems with varying thickness due to the use of a feather pen. The scores of these two authors, and others of less importance in the ACM, are characterized by the presence of frontispieces, located at the beginning of the first page in Sanz style scores, and at the beginning of each voice (two voices per page) in Britto style scores. In both cases, the lyrics (text) of the song are present. The text can be located above or below the staff, and its presence must be taken into account during the preprocessing stage.
The structure of the paper follows the different stages of the OMR system implemented, which extends the description shown in [7, 9], a scheme is shown in Figure 2. Thus, the organization of the paper is the following. Section 2 describes the image preprocessing stage, which aims to eliminate or reduce some of the problems related to the coding of the material and the quality of the acquisition process. The main steps of the image preprocessing stage are explained in the successive subsections: selection of the area of interest, conversion of the color-space, compensation of illumination, binarization and correction of the image rotation. Section 3 shows the process of detection and blanking the staff lines. Blanking the staff lines properly appears to be a crucial stage for the correct extraction of the music symbols. Section 4 presents the method defined to extract complex music symbols. Finally, the classification of the music symbols is performed as explained in Section 5. The evaluation of the OMR system is presented in Section 6. Section 7 describes the method used to generate a computer representation of the music content extracted by the OMR system. Finally, some conclusions are drawn in Section 8.
2. Image Preprocessing
The digital images of the scores to process suffer several types of degradations that must be considered. On one hand, the scores have marks and blots that hide the original symbols; the papers are folded and have light and dark areas; the color of the ink varies appreciably through a score; the presence of fungi or mold affects the general condition of the sheet, an so forth. On the other hand, the digitalization process itself may add further degradations to the digital image. These degradations can take the form of strange objects that appear in the images, or they may also be due to the wrong alignment of the sheets in the image. Moreover, the irregular leveling of the pages (a common situation in the thickest books) often creates illumination problems. Figure 3 shows some examples of these common imperfections.
A careful preprocessing procedure can significantly improve the performance of the recognition process. The preprocessing stage considered in our OMR system includes the following steps.
-
(a)
selection of the area of interest and elimination of nonmusical elements,
-
(b)
grayscale conversion and illumination compensation,
-
(c)
image binarization,
-
(d)
correction of image rotation.
These steps are implemented in different stages, applying the procedures to both the whole image and to parts of the image to get better results. The following subsections describe the preprocessing stages implemented.
2.1. Selection of the Area of Interest and Elimination of Nonmusical Elements
In order to reduce the computational burden (reducing the total amount of pixels to process) and to obtain relevant intensity histograms, an initial selection of the area of interest is done to remove parts of the image that do not contain the score under analysis. A specific region of interest ROI extraction algorithm [10] has been developed. After the user manually draws a polygon surrounding the area of interest, the algorithm returns the minimal rectangle containing this image area (Figure 4).
After this selection, an initial removal of the nonmusical elements is carried out. In many scores, some forms of aesthetic embellishments (frontispieces) are present in the initial part of the document which can negatively affect the entire OMR process. These are color elements that are removed using the hue of the pixels (Figure 5).
2.2. Grayscale Conversion and Illumination Compensation
The original color space of the acquired images is RGB. The musical information of the score is contained in the position and shapes of the music symbols, but not in their color, so the images are converted to grayscale. The algorithm is based on the HSI (Hue, Saturation, Lightness, Intensity) model and, so, the conversion implemented is based on a weighted average [10]:

where  ,
,  and
and  are the coordinates of the color of each pixel.
are the coordinates of the color of each pixel.
Now, the process of illumination compensation starts. The objective is to obtain a more uniform background so that the symbols can be more efficiently detected. In our system, the illumination cannot be measured, it must be estimated from the available data.
The acquired image  is considered to be the product of the reflectance
is considered to be the product of the reflectance  and illumination
and illumination  fields [11]:
fields [11]:

The reflectance  measures the light reflection characteristic of the object, varying from
measures the light reflection characteristic of the object, varying from  , when the surface is completely opaque, to
, when the surface is completely opaque, to  [12]. The reflectance contains the musical information.
[12]. The reflectance contains the musical information.
The aim is to obtain an estimation  of the illumination
of the illumination  to obtain a corrected image
to obtain a corrected image  according to [11].
according to [11].

In order to estimate  , the image is divided into a regular grid of cells, then, the average illumination level is estimated for each cell (Figure 6). Only the background pixels of each cell are used to estimate the average illumination levels. These pixels are selected using the threshold obtained by the Otsu method [13] in each cell.
, the image is divided into a regular grid of cells, then, the average illumination level is estimated for each cell (Figure 6). Only the background pixels of each cell are used to estimate the average illumination levels. These pixels are selected using the threshold obtained by the Otsu method [13] in each cell.
Example of compensation of the illumination. (a) original image (grayscale); (b) grid for the estimation of the illumination ( cells), the location of the data points used to interpolate the illumination mask is marked; (c): average illumination levels of each cell; (d): illumination mask with interpolated illumination levels.
cells), the location of the data points used to interpolate the illumination mask is marked; (c): average illumination levels of each cell; (d): illumination mask with interpolated illumination levels.
The next step is to interpolate the illumination pattern to the size of the original image. The starting points for the interpolation precess are placed as shown in Figure 6. The algorithm used is a bicubic piecewise interpolation with a neighborhood of 16 points which gives a smooth illumination field with continuous derivative [14]. Figure 6 shows the steps performed for the compensation of the illumination.
2.3. Image Binarization
In our context, the binarization aims to distinguish between the pixels that constitute the music symbols and the background. Using the grayscale image obtained after the process described in the previous section, a threshold  , with
, with  , must be found to classify the pixels as background or foreground [10].
, must be found to classify the pixels as background or foreground [10].
Now, the threshold must be defined. The two methods employed in our system are the iterative average method [10] and the Otsu method [13], based on a deterministic and a probabilistic approach, respectively.
Figure 7 shows an example of binarization. Observe that the results do not show marked differences. So, in our system, the user can select the binarization method at the sight of their performance on each particular image, if desired.
2.4. Correction of Image Rotation
The staff lines are a main source of information of the extent of the music symbols and their position. Hence, the processes of detection and extraction of staff lines are, in general, an important stage of an OMR system [9]. In particular, subsequent procedures are simplified if the lines are straight and horizontal. So, a stage for the correction of the global rotation of the image is included. Note that other geometrical corrections [15] have not been considered.
The global angle of rotation shown by the staff lines must be detected and the image must be rotated to compensate such angle. The method used for the estimation of the angle of rotation makes use of the Hough transform. Several implementations of this algorithm have been developed for different applications and the description can be found in a number of [16–18]. The Hough transform is based on a linear transformation from a standard  reference plane to a distance-slope one
reference plane to a distance-slope one  with
with  and
and  . The (
. The ( ,
, ) plane, also known as Hough plane, shows some very important properties [18].
) plane, also known as Hough plane, shows some very important properties [18].
-
(1)
a point in the standard plane corresponds to a sinusoidal curve in the Hough plane,
-
(2)
a point in the Hough plane corresponds to a straight line in the standard plane,
-
(3)
points of the same straight line in the standard plane correspond to sinusoids that share a single common point in the Hough plane.
In particular, property ( ) can be used to find the rotation angle of the image. In Figure 8, the Hough transform of an image is shown where two series of large values in the Hough plane, corresponding to the values
) can be used to find the rotation angle of the image. In Figure 8, the Hough transform of an image is shown where two series of large values in the Hough plane, corresponding to the values  18
18 and
and  27
27 , are observed. These values correspond to the vertical and horizontal alignments, respectively. The first set of peaks (
, are observed. These values correspond to the vertical and horizontal alignments, respectively. The first set of peaks ( 18
18 ) corresponds to the vertical stems of the notes; the second set of peaks (
) corresponds to the vertical stems of the notes; the second set of peaks ( 27
27 ) corresponds to the approximately horizontal staff lines. In the Hough plane, the
) corresponds to the approximately horizontal staff lines. In the Hough plane, the  dimension is discretized with resolution of 1 degree, in our implementation.
dimension is discretized with resolution of 1 degree, in our implementation.
Once the main slope is detected, the difference with  is computed, and the image is rotated to correct its inclination. Such procedure is useful for images with global rotation and low distortion. Unfortunately, most of the images of the scores under analysis have distortions that make the staff appear locally rotated. In order to overcome this inconvenience, the correction of the rotation is implemented only if the detected angle is larger than
is computed, and the image is rotated to correct its inclination. Such procedure is useful for images with global rotation and low distortion. Unfortunately, most of the images of the scores under analysis have distortions that make the staff appear locally rotated. In order to overcome this inconvenience, the correction of the rotation is implemented only if the detected angle is larger than  . In successive steps of the OMR process, the rotation of portions of each single staff is checked and corrected using the technique described here.
. In successive steps of the OMR process, the rotation of portions of each single staff is checked and corrected using the technique described here.
3. Staff Processing
In this section, the procedure developed to detect and remove the staff lines is presented. The whole procedure includes the detection of the staff lines and their removal using a line tracking algorithm following the characterization in [19]. However, specific processes are included in our implementation, like the normalization of the score size and the local correction of rotation. In the next subsections, the stages of the staff processing procedure are described.
3.1. Isolation of the Staves
This task involves the following stages.
-
(1)
estimation of the thickness of the staff lines,
-
(2)
estimation of the average distance between the staff lines and between staves,
-
(3)
estimation of the width of the staves and division of the score,
-
(4)
revision of the staves extracted.
In order to compute the thickness of the lines and the distances between the lines and between the staves, a useful tool is the so called row histogram or  -projection [7, 20]. This is the count of binary values of an image, computed row by row. It can be applied to both black foreground pixels and white background pixels (see Figure 9). The shape of this feature and the distribution of its peaks and valleys, are useful to identify the main elements and characteristics of the staves.
-projection [7, 20]. This is the count of binary values of an image, computed row by row. It can be applied to both black foreground pixels and white background pixels (see Figure 9). The shape of this feature and the distribution of its peaks and valleys, are useful to identify the main elements and characteristics of the staves.
3.1.1. Estimation of the Thickness of the Staff Lines
Now, we consider that the preliminary corrections of image distortions are sufficient to permit a proper detection of the thickness of the lines. In Figure 10, two examples of the shape of row histograms for distorted and corrected images of the same staff are shown. In Figure 10(a), the lines are widely superimposed and their discrimination is almost impossible, unlike the row histogram in Figure 10(b).
A threshold is applied to the row histograms to obtain the reference values to determine the average thickness of the staff lines. The choice of the histogram threshold should be automatic and it should depend on the distribution of black/white values of the row histograms. In order to define the histogram threshold, the overall set of histogram values are clustered into three classes using K-means [21] to obtain the three centroids that represent the extraneous small elements of the score, the horizontal elements different from the staff lines, like the aligned horizontal segments of the characters, and the effective staff lines (see Figure 11). Then, the arithmetic mean between the second and the third centroids defines the histogram threshold.
The separation between consecutive points of the row histogram that cut the threshold (Figure 12) are, now, used in the K-means clustering algorithm [21] to search for two clusters. The cluster containing more elements will define the average thickness of the five lines of the staff. Note that the clusters should contain five elements corresponding to the thickness of the staff lines and four elements corresponding the the distance between the staff lines in a staff.
Example of the process of detection of the thickness of the lines. For each peak (in the image only the first peak is treated as example), the distance between the two points of intersection with the fixed threshold is computed. The distances extracted are used in a K-means clustering stage, with two clusters, to obtain a measure of the thickness of the lines of the whole staff.
3.1.2. Estimation or the Average Distance between the Staff Lines and between the Staves
In order to divide the score into single staves, both the average distance among the staff lines and among the staves themselves must be computed. Figure 13 shows an example of the row histogram of the image of a score where the parameters described are indicated.
In this case, the K-means algorithm [21] is applied to the distances between consecutive local maxima of the histogram over the histogram threshold to find two clusters. The centroids of these clusters, represent the average distance between the staff lines and the average distance between the staves. The histogram threshold is obtained using the technique described in the previous task (task 1) of the isolation of staves procedure).
3.1.3. Estimation of the Width of the Staff and Division of the Score
Now the parameters described in the previous stages are employed to divide the score into its staves. Assuming that all the staves have the same width for a certain score, the height of the staves is estimated using:

where  ,
,  ,
,  and
and  stand for the staff width, the thickness of the lines, the distance between the staff lines and the distance between the staves, respectively. In Figure 14, it can be observed how these parameters are related to the height of the staves.
stand for the staff width, the thickness of the lines, the distance between the staff lines and the distance between the staves, respectively. In Figure 14, it can be observed how these parameters are related to the height of the staves.
Example of the usage of the row histogram of the white pixels to detect errors in the computation of the staff position. In (a), the staff is correctly extracted and the first and the last row histogram values are equal to the maximum. In (b), the staff is badly cut and the value of the histogram of the last row is smaller than the maximum value.Row histogram of the white pixels for a correctly extracted staffRow histograms of the white pixels for an incorrectly extracted staff
As mentioned before, rotations or distortions of the original image could lead to a wrong detection of the line thickness and to the fail of the entire process. In order to avoid such situation, the parameters used in this stage are calculated using a central portion of the original image. The original image is divided into 16 cells and only the central part (4 cells) is extracted. The rotation of this portion of the image is corrected as described in Section 2.4, and then, the thickness and width parameters are estimated.
3.1.4. Revision of the Staves Extracted
In some handwritten music scores, the margins of the scores do not have the same width and the extraction procedure can lead to a wrong fragmentation of the staves. When the staff is not correctly cut, at least one of the margins is not completely white, conversely, some black elements are in the margins of the image selected. In this case, the row histogram of white pixels can be used to easily detect this problem by simply checking the first and the last values of the white row histogram (see Figures 15(a) and 15(b)), and comparing these values versus the maximum. If the value of the first row is smaller than the maximum, the selection window for that staff is moved up one line. Conversely, if the value of the last row of the histogram is smaller than the maximum, then the selection window for that staff is moved down on line. The process is repeated until a correct staff image, with white margins and containing the whole five lines is obtained.
3.2. Scaling of the Score
In order to normalize the dimensions of the score and the descriptors of the objects before any recognition stage, a scaling procedure is considered. A reference measure element is required in order to obtain a global scaling value for the entire staff. The most convenient parameter is the distance between the staff lines. A large set of measures have been carried out on the available image samples and a reference value of  pixels has been decided. The scaling factor
pixels has been decided. The scaling factor  , between the reference value and the current lines distance is computed by
, between the reference value and the current lines distance is computed by

where  is the distance between the lines of the staff measured as described in Section 3.1.2. The image is interpolated to the new size using the nearest neighbor interpolation method (zero order interpolation) [22].
is the distance between the lines of the staff measured as described in Section 3.1.2. The image is interpolated to the new size using the nearest neighbor interpolation method (zero order interpolation) [22].
3.3. Local Correction of the Rotation
In order to reduce the complexity of the recognition process and the effect of distortions or rotations, each staff is divided vertically into four fragments (note that similar approaches have been reported in the literature [20]). The fragmentation algorithm locates the cutting points so that no music symbols are cut. Also, it must detect non musical elements (see Figure 16), in case they have not been properly eliminated.
Vertical division of the staves. Sample staff with optimal vertical divisions (dashed line) Column histogram of the black pixels. The threshold (solid line), the minima under the threshold (circles), the line that divide the staff in equal parts (thick line) and the optimal division lines found (dashed lines) are shown. The arrows show the shift from the initial position of the division lines to their final location.
The procedure developed performs the following steps.
-
(1)
split the staff into four equal parts and store the three splitting points,
-
(2)
compute the column histogram (
 -projection) [7],
-projection) [7], -
(3)
set a threshold on the column histogram as a multiple of the thickness of the staff lines estimated previously,
-
(4)
locate the minimum of the column histogram under the threshold (Figure 16(b)),
-
(5)
select as splitting positions the three minima that are the closest to the three points selected at step (
 ).
).
This stage allows to perform a local correction of the rotation for each staff fragment using the procedure described in Section 2.4 (Figure 17). The search for the rotation angle of each staff fragment is restricted to a range around  (horizontal lines): from
(horizontal lines): from  to
to  .
.
3.4. Blanking of the Staff Lines
The staff lines are often an obstacle for symbol tagging and recognition in OMR systems [23]. Hence, a specific staff removal algorithm has been developed. Our blanking algorithm is based on tracking the lines before their removal. Note that the detection of the position of the staff lines is crucial for the location of music symbols and the determination of the pitch. Notes and clefs are painted over the staff lines and their removal can lead to partially erase the symbols. Moreover, the lines can even modify the real aspect of the symbols filling holes or connecting symbols that have to be separated. In the literature, several distinct methods for line blanking can be found [24–30], each of them with a valid issue in the most general conditions, but they do not perform properly when applied to the scores we are analyzing. Even the comparative study in [19] is not able to find a clear best algorithm.
The approach implemented in this work uses the row histogram to detect the position of the lines. Then, a moving window is employed to track the lines and remove them. The details of the process are explained through this section.
To begin tracking the staff lines, a reference point for each staff line must be found. To this end, the approach shown in Section 3.1.1 is used: the row histogram is computed on a portion of the staff, the threshold is computed and the references of the five lines are retrieved.
Next, the lines are tracked using a moving window of twice the line thickness plus 1 pixel of height and 1 pixel of width (Figure 18). The lines are tracked one at a time. The number of black pixels within the window is counted, if this number is less than twice the line thickness, then the window is on the line, the location of the staff line is marked, according to the center of the window, and, then, the window is shifted one pixel to the right. Now, the measure is repeated and, if the number of black pixels keeps being less than twice the thickness of the line, the center of mass of the group of pixels in the window is calculated and the window is shifted vertically 1 pixel towards it, if necessary. The vertical movement of the window is set to follow the line and it is restricted so as not to follow the symbols. Conversely, if the number of black pixels is more than twice the line thickness, then the window is considered to be on a symbol, the location of the staff line is marked and the window is shifted to the right with no vertical displacement.
Now, the description of the process of deletion of the staff lines follows: if two consecutive positions of the analysis window reveal the presence of the staff line, the group of pixels of the window in the first position is blanked, then the windows are shifted one pixel to the right and the process continues. This approach has shown very good performance for our application in most of cases. Only when the thickness of the staff lines presents large variations, the process leaves a larger number of small artifacts. In Figure 19, an example of the application of the process is shown.
4. Processing of Music Symbols
At this point, we have a white and black image of each staff without the staff lines, the music symbols are present together with artifacts due to parts of the staff lines not deleted, spots, and so forth. The aim of the procedure described in this section is to isolate the sets of black pixels that belong to the musical symbols (notes, clefs, etc.), putting together the pieces that belong to the same music symbol. Therefore, two main steps can be identified: isolation of music elements and combination of elements that belong to the same music symbol. These steps are considered in the following subsections.
4.1. Isolation of Music Elements
The isolation process must extract the elements that correspond to music symbols or parts of music symbols and to remove the artifacts. The nonmusical elements may be due to staff line fragments not correctly removed in the blanking stage, text or other elements like marks or blots. The entire process can be split into two steps.
-
(1)
tagging of elements,
-
(2)
removal of artifacts.
4.1.1. Tagging of Elements
An element is defined as a group of pixels isolated from their neighborhood. Each of these groups is tagged with a unique value, the pixel connectivity rule [31] is employed to detect the elements using the 4-connected rule.
4.1.2. Removal of Artifacts
Small fragments coming from an incomplete removal of the staff lines, text and other elements must be removed before starting the classification of the tagged object. This task performs two different tests.
The elements, that are smaller than the dot (the music symbol for increasing half the value of a note) are detected and removed. The average size is fixed a priori, evaluating a set of the scores to be recognized and using the distance between staff lines as reference. Now, other elements (text in most cases) generally located at the edges of the staff will be removed. The top and the bottom staff lines are used as reference; if there is any element beyond this lines, it is checked if the element is located completely outside the lines, then, it is removed. An example of the performance of this strategy is shown in Figure 20.
4.2. Combination of Elements Belonging to the Same Music Symbol
At this stage, we deal a number of music symbols composed by two or more elements, spatially separated and with different tags. In order to properly feed the classifier, the different parts of the same symbol must be joined and a single tag must be given.
The process to find the elements that belong to the same music symbol is based on the calculation of the row and column histograms for each pair of tagged objects and the detection of the common parts of them. After a pair of objects that share parts of their projections is found, the elements are merged together (see Figure 21), a single tag is assigned and the process continues.
There are cases, as the double whole (breve) or the key of  , that are characterized by the presence of two or more horizontal bands (Figure 22). The strategy used to merge such symbols is similar to the one employed before. The two bands of a double whole will show a nearly coincident column histogram, while their row histograms will be almost completely separated (Figure 23); hence, the check of the overlap of both histograms is not sufficient. Then, the overlap of the column histograms is checked measuring the separation of the two maxima. This separation must be below a threshold and, conversely, the row histograms must show a null overlap to merge this objects (Figure 23).
, that are characterized by the presence of two or more horizontal bands (Figure 22). The strategy used to merge such symbols is similar to the one employed before. The two bands of a double whole will show a nearly coincident column histogram, while their row histograms will be almost completely separated (Figure 23); hence, the check of the overlap of both histograms is not sufficient. Then, the overlap of the column histograms is checked measuring the separation of the two maxima. This separation must be below a threshold and, conversely, the row histograms must show a null overlap to merge this objects (Figure 23).
In spite of these processes, the classifier will receive some symbols that do not correspond to real music symbol, hence, the classifier should be able to perform a further inspection based on the possible coherence of the notation and, as suggested in [32, 33], on the application of music laws.
5. Classification
At this stage, the vectors of features extracted for the unknown symbols must be compared against a series of patterns of known symbols. The classification strategy and the features to employ have to be decided. In this section, the features that will be used for the classification are described. Then, the classifiers employed are presented [31, 34]. Finally, the task of identification of the location of the symbols is considered.
5.1. Extraction of Features of Music Symbols
A common classification strategy is based on the comparison of the numerical features extracted for the unknown objects with a reference set [17]. In an OMR system, the objects are the music symbols, isolated and normalized by the preceding stages, then a set of numerical features must be extracted from them to computationally describe these symbols [35, 36]. In this work, four different types of features have been chosen. These features are based on:
-
(1)
fourier descriptors,
-
(2)
bidimensional wavelet transform coefficients,
-
(3)
bidimensional Fourier transform coefficients,
-
(4)
angular-radial transform coefficients.
These descriptors will be extracted from the scaled music symbols (See Section 3.2) and used in different classification strategies, with different similarity measures.
5.1.1. Fourier Descriptors
The Fourier transform of the set of coordinates of the contour of each symbol is computed to retrieve the vector of Fourier descriptors which is an unidimensional robust and reliable representation of the image [37]. The low frequency components represent the shape of the object, while the highest frequency values follow the finest details. The vector of coordinates of the contour of the object (2D) must be transformed into a unidimensional representation. Two options are considered to code the contour.
-
(1)Distance
to the centroid:
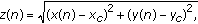 (6)
(6) -
(2)complex
coordinates with respect to the centroid:
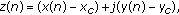 (7)
(7)
where  and
and  are the coordinates of the centroid and
are the coordinates of the centroid and  and
and  are the coordinates of the n th point of the contour of the symbol. The Fourier descriptors are widely employed in the recognition of shapes, where the invariance with respect to geometrical transformations and invariance with respect to changes of the initial point selected for tracking the contour are important. In particular, the zero frequency coefficient corresponds to the centroid, so a normalization of the vector of coordinates by this value gives invariance against translation. Also, the normalization of the coefficients with respect to the first coefficient can provide invariance against scaling. Finally, if only the modulus of the coefficients is observed, invariance against rotation and against changes in the selection of the starting point of the edge vector contour is achieved.
are the coordinates of the n th point of the contour of the symbol. The Fourier descriptors are widely employed in the recognition of shapes, where the invariance with respect to geometrical transformations and invariance with respect to changes of the initial point selected for tracking the contour are important. In particular, the zero frequency coefficient corresponds to the centroid, so a normalization of the vector of coordinates by this value gives invariance against translation. Also, the normalization of the coefficients with respect to the first coefficient can provide invariance against scaling. Finally, if only the modulus of the coefficients is observed, invariance against rotation and against changes in the selection of the starting point of the edge vector contour is achieved.
For the correct extraction of these features, the symbols must be reduced to a single black element, with no holes. To this end a dilation operator is applied to the symbols to fill the white spaces and holes (Figure 24), using a structural element fixed a priori for each type of the music notations considered. However, the largest holes may still remain (as in the inner part of the G clef, see Figure 25(b)). Hence, all the edges are tracked using a backtracking bug follower algorithm [17], their coordinates are retrieved and the smaller contours are removed.
5.1.2. Bidimensional Wavelet Transform Coefficients
The wavelet transform is based on the convolution of the original signal with a defined function with a fixed shape (the mother function) that is shifted and scaled to best fit the signal itself [10]. After applying the transformation, some coefficients will be used for the classification. In our case, the mother wavelet will be the CDF 5/3 biorthogonal wavelet (Cohen-Daubechies-Feauveau), also called the LeGall 5/3, widely used in JPEG 2000 lossless compression [38]. The coefficients are obtained computing the wavelet transform of each symbol framed in its tight bounding box. Only the coefficients with the most relevant information are kept. This selection is done taking into account both the frequency content (the first half of the coefficients) and their absolute value (the median of the absolute value of the horizontal component). Finally, the coefficients are employed to compute the following measures used as descriptors: sum of absolute values, energy, standard deviation, mean residual and entropy.
5.1.3. Bidimensional Fourier Transform Coefficients
As the wavelet transform, the Fourier transform is used to obtain a bidimensional frequency spectrum. The coefficients of the transform are selected depending on their magnitude and a series of measures are obtained (as in Section 5.1.2). Note that, according to the comments in Section 5.1.1, only the modulus of the coefficients is taken into account.
5.1.4. Angular-Radial Transform Coefficients
The angular radial transform is a region-based shape descriptor that can represent the shape of an object (even a holed one) using a small number of coefficients [39]. The transform rests on a set of basis functions  , that depend on two main parameters (
, that depend on two main parameters ( and
and  ) related to an angle (
) related to an angle ( ) and a radius (
) and a radius ( ) value. In our case,
) value. In our case,  angular functions and
angular functions and  radial functions are built to define
radial functions are built to define  basis functions. Then, each basis function is iteratively integrated for each location of the image of the symbol to obtain a total amount of
basis functions. Then, each basis function is iteratively integrated for each location of the image of the symbol to obtain a total amount of  descriptors (the first one is used to normalize the others). In order to speed up the extraction of the coefficients, a LUT (look-up table) approach is employed [40].
descriptors (the first one is used to normalize the others). In order to speed up the extraction of the coefficients, a LUT (look-up table) approach is employed [40].
In order to calculate the coefficients, the image is represented in a polar reference system with origin located at the position of the centroid of the symbol. Then, a minimum circle, to be used by the transform procedure (see Figure 26) [39], is defined as the smallest circle that completely contains the symbol. The centroid has been computed in two different ways: as the centroid of the contour of the symbol and as the center of the bounding box. This leads to two different sets of angular-radial transform coefficients: ART1 and ART2, respectively.
5.2. Classifiers
5.2.1. K-NN Classification
The k-NN classifier is one of the simplest ones, with asymptotically optimal performance. The class membership of an unknown object is obtained computing the most common class among the  nearest known elements, for a selected distance measure. Note that the performance of the procedure depends on the number of training members of each class [31].
nearest known elements, for a selected distance measure. Note that the performance of the procedure depends on the number of training members of each class [31].
For our classifier, the statistics of order one and two of each feature and for each class of symbol are computed. The features that do not allow to distinguish among different classes are rejected.
The two sets of Fourier descriptors (Section 5.1.1) are entirely included, leading to the two sets of  features. Similarly, the whole two sets of
features. Similarly, the whole two sets of  coefficients obtained by the angular-radial transform (Section 5.1.4) are kept. The first three parameters obtained by the bidimensional wavelet transform (Section 5.1.2) are used: the two energy related measures and its standard deviation, because they are the only ones showing a reasonable reliability for the discrimination of classes. Finally, only the sum of the absolute values of the bidimensional Fourier transform (Section 5.1.3) is retained, for the same reason.
coefficients obtained by the angular-radial transform (Section 5.1.4) are kept. The first three parameters obtained by the bidimensional wavelet transform (Section 5.1.2) are used: the two energy related measures and its standard deviation, because they are the only ones showing a reasonable reliability for the discrimination of classes. Finally, only the sum of the absolute values of the bidimensional Fourier transform (Section 5.1.3) is retained, for the same reason.
The two distance measures employed are
-
(i)square
residuals, for Fourier descriptors:
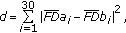 (8)
(8)where
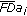 and
and 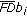 are the Fourier descriptors of the unknown symbol
are the Fourier descriptors of the unknown symbol  and the training one
and the training one 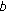 ,
, -
(ii)absolute
residuals of the angular-radial, wavelet and Fourier transforms:
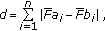 (9)
(9)where
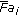 and
and 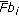 are the angular-radial transform coefficients (
are the angular-radial transform coefficients (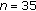 ), the wavelet transform coefficients (
), the wavelet transform coefficients (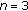 ) or the single parameter selected from the Fourier transform (
) or the single parameter selected from the Fourier transform (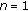 ), for the unknown element
), for the unknown element  and the training element
and the training element 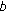 .
.
5.2.2. Classifiers Based on Mahalanobis Distance
The Mahalanobis distance [41] is used in a classification procedure to measure the distance of the feature vector of an object to the centroid of each class. The definition of this measure rest on the dissimilarity measure between two multidimensional random variables, calculated using the covariance matrix  as
as

where the distance is computed between the features vector  of the unknown symbol and the centroid
of the unknown symbol and the centroid  of the class
of the class  .
.
Note that the inverse of  is required, so
is required, so  must be nonsingular. To this end, the number of training elements with linear independence of each class should not be smaller than the dimension of the feature vector. Since there are some rare (not commonly used) musical objects in the data available, a reduced number of features is required. We have selected
must be nonsingular. To this end, the number of training elements with linear independence of each class should not be smaller than the dimension of the feature vector. Since there are some rare (not commonly used) musical objects in the data available, a reduced number of features is required. We have selected  features, among the ones with the smallest variance within a class, to guarantee that
features, among the ones with the smallest variance within a class, to guarantee that  exists.
exists.
5.2.3. Classifiers Based on the Fisher Linear Discriminant
The Fisher linear discriminant approach is based on the search of a linear combination of the vector of features such that the dissimilarity between two classes is as large as possible [31]. In particular, the Fisher linear discriminant aims to represent two clouds of multidimensional vectors in a favorable unidimensional framework [42]. To this end, a projection vector  , for the vectors of features
, for the vectors of features  is found, such that the projections
is found, such that the projections  form two clouds of elements of the two classes, projected on a line, such that the lines distance is as large as possible. Then, the membership of an unknown symbol (vector of features) is derived from the location of its projection. In particular, a k-NN approach can be used and it can also be assumed that the projections of the vectors of features follow a Gaussian distribution [42]. This model can be used to compute the probability that a certain projection belongs to a certain distribution (class). Both approaches are implemented in this work.
form two clouds of elements of the two classes, projected on a line, such that the lines distance is as large as possible. Then, the membership of an unknown symbol (vector of features) is derived from the location of its projection. In particular, a k-NN approach can be used and it can also be assumed that the projections of the vectors of features follow a Gaussian distribution [42]. This model can be used to compute the probability that a certain projection belongs to a certain distribution (class). Both approaches are implemented in this work.
Note that the Fisher linear discriminant is defined in a two-class framework whilst an OMR system aims to recognize the proper symbol among several classes, so, an exhaustive search for the class membership is done.
5.2.4. Building the Training Database
About eighty scores written in white mensural notation in the two styles considered (Stephano di Britto and Maestro Sanz notation styles) have been analyzed. These scores contain more than  isolated music symbols. About
isolated music symbols. About  of the scores are written with the style of di Britto and about
of the scores are written with the style of di Britto and about  of the scores of each style correspond to these two authors. Note that we have not found significative differences in the results and the features obtained for these main authors with respect to the results and features obtained for others. A minimum of
of the scores of each style correspond to these two authors. Note that we have not found significative differences in the results and the features obtained for these main authors with respect to the results and features obtained for others. A minimum of  samples of the less common symbols (classes) are stored. When the samples of a certain class are not enough to reach the lower limit of
samples of the less common symbols (classes) are stored. When the samples of a certain class are not enough to reach the lower limit of  , the necessary elements are generated artificially using nonlinear morphological operations.
, the necessary elements are generated artificially using nonlinear morphological operations.
5.3. Locating the Symbol Position (Pitch)
The final task related to the recognition of music symbols is the determination of the position of each of them in the staff. Note that, at this stage, the accurate tracking of the staff lines has already been performed and their positions, throughout the whole staff, are known.
The exact positions of the lines and the spaces of the staves must be defined. The spaces between the staff lines are located according to the following relation:  , where
, where  stands for the location of the
stands for the location of the  th space,
th space,  represents the position of the
represents the position of the  th line and
th line and  is the separation between consecutive staff lines. Then, the row histogram of the black pixels of each extracted symbol is computed using a tight bounding box. This histogram is aligned with the staff at the right position. Then, the maximum of the histogram is located and the staff line or the space between staff lines closest to the location of this maximum is used to define the location of the symbol under analysis (Figure 27).
is the separation between consecutive staff lines. Then, the row histogram of the black pixels of each extracted symbol is computed using a tight bounding box. This histogram is aligned with the staff at the right position. Then, the maximum of the histogram is located and the staff line or the space between staff lines closest to the location of this maximum is used to define the location of the symbol under analysis (Figure 27).
Example of the determination of the line/space membership of a quarter-note (in gray) for pitch detection. The row histogram of the black pixels of the note (dashed line) shows a maximum close to the third line, identified by the third peak of the row histogram of the black pixels of the staff (solid line).
Observe that there exist two classes of symbols for which the position is not relevant: the longa silence and the C clef.
Also note that other alternatives could be used to determine the pitch of the symbols. For example, the location of the bounding box in the scaled score together with the location and shape of the model of the symbol in the box would be enough to accomplish this task.
6. Evaluation of the System Performance
Two main tasks are directly related to the global success of the recognizer: the extraction and the classification of the symbols. Thus, the evaluation of the OMR system is based on the analysis of the results of these two stages.
6.1. Performance Evaluation of the Algorithm of Symbol Extraction
The main source of errors of the extraction stage is the process of blanking the staff lines [43]. When the staff lines are not correctly blanked, undesired interconnections between objects appear, which lead to the extraction of strange symbols, whose shape cannot be recognized at all (Figure 28). Such problem is much more frequent in Sanz style samples, but this seems to be due to the worse conditions of the scores that use this notation style. In Table 1, the success rates in the extraction process are shown. The "symbols correctly extracted" do not show any blot or mark, the "symbols extracted with errors" show some black pixels or lines fragments and, finally, the "symbols completely lost" are the ones the algorithm is not able to detect at all.
Both, the symbols correctly extracted and the ones extracted with errors are included in the evaluation of the classifier, as described in the next sections.
6.2. Implementation Results of the k-NN Classifier
The k-NN classifier works with the set of Fourier descriptors that uses the distance of the contour points to the centroid, a fixed percentage of the wavelet transform coefficients, the Fourier transform coefficients and the two sets of angular-radial transform coefficients. Three different values of neighbors  have been employed: 1, 3, and 5. In Table 2, the correct classification rates are shown.
have been employed: 1, 3, and 5. In Table 2, the correct classification rates are shown.
The results are generally better for the scores that use the notation style of Britto than for the ones that use Sanz notation style. This is mainly due to the generally lower quality of arts of the scores written in Sanz notation style and, also, to the different discrimination capabilities of the features when applied to different notation styles.
In general, the Fourier descriptors used show good performance, showing the best results for symbols hardly recognizable, and partially extracted. This is mainly due to the approach used for the selection of the largest object in the framework, based on the contours (Section 5.1.1). The wavelet coefficients seem to be more heavily influenced by the worst conditions of Sanz style scores, but the classifier attains reasonable results when using the k-NN method. Recall that the k-NN shows a high degree of dependence on the robustness of the features employed. This is the reason for the poor results obtained using the Fourier transform coefficients, when only one feature is used (Section 5.2.1). Finally, the results of the k-NN classifier implemented with the angular-radial transform (ART) coefficients are the best ones. The method that uses the centroid computed as the center of gravity of the contour of the objects shows slightly better classification rates than the approach that uses the center of the bounding box of the object.
6.3. Implementation Results of the Classifier Based on the Mahalanobis Distance
As mentioned before, the calculation of the Mahalanobis distance depends on the size of the matrix of features. In order to assure the nonsingularity of the covariance matrix, the number of features employed was reduced to twelve due to the amount of available data and limited by some rare symbols. The reduction of the number of features employed led, in our opinion, to a degradation of the general performance of the method. For this reason, only the process based on the angular-radial transform coefficients returns acceptable results. In Table 3, the correct classification rates for the Mahalanobis approach implemented with the ART coefficients are shown.
Better results would be expected if more training elements of all the classes were available, thus allowing to use larger vectors of features in this procedure.
6.4. Implementation Results of the Fisher Linear Discriminant
As in the case of the Mahalanobis classifier, the need of the inverse of the covariance matrix forces to reduce the number of usable features. Two strategies are used to decide the membership of the unknown element after the projection of its vector of features: the k-NN classification and the Gaussian approach. The Fourier descriptors show acceptable results only when the Gaussian approach is used. The results are shown in Table 4.
Again, the results obtained using the angular radial transform coefficients with reference at the center of gravity of the contour ART1 are better than the alternative approaches. Note that there is no marked difference between the k-NN and the Gaussian method of classification using the projections of the vectors of features.
7. Computer Music Representation
After all the stages of the OMR system are completed (Figure 2), the recognized symbols can be employed to write down the score in different engraving styles or even to make it sound. Nowadays, there is no real standard for computer symbolic music representation [8], although different representation formats (sometime linked to certain applications) are available. Among them, MusicXML [44] is a format to represent western music notation from the 17th century onwards. WEDELMUSIC [45] is a XML compliant format which can include the image of the score and an associated WAV or MIDI file and it is mainly aimed to support the development of new emerging applications. GUIDO [46] is a general purpose language for representing scores. More recently, MPEG-SMR (Symbolic Music Representation) [47] aims to become a real standard to cope with computer music representation and the related emerging needs of new interactive music applications.
In our case, we have selected Lilypond [48] for music engraving. This program, and associated coding language, is part of the GNU project and accepts an ASCII input to engrave the score. It determines the spacing by itself, and breaks lines and pages to provide a tight and uniform layout. An important feature in our context is that it can draw the score in modern notation and, with minimum changes, the score in white mensural notation can also be obtained [49]. Additionally, the program can also generate the MIDI file of the typed score [50] so that the recognized score can be listened.
We will show an example of the usage of this tool. In Figure 29, a sample piece of a four voices work is shown. In Figure 30, sample code to obtain the transcription of the score using both the original notation and modern notation is shown (Figure 31). Observe that the text that describes the music symbols and pitches is virtually the same for both types of notation. When the score is to be written in white mensural notation, Figure 30(a), the code for Lilypond can be directly obtained from the output of the OMR process described since there is a one-to-one relation between the music symbol-pitch recognized and the code required to describe that symbol-pitch in Lilypond. If the target score must be written using modern notation, some slight changes must be done in order to properly fill the measures maintaining the correct duration of the notes. For example, observe, in Figure 30(b), how the last note of the soprano voice (brevis in white mensural notation) has been written as a quarter-note tied to a whole-note tied to a half-note-dot, instead of as a square note (a square note  two whole notes). These changes need to be done by hand since the version of Lilypond employed does not make such corrections automatically.
two whole notes). These changes need to be done by hand since the version of Lilypond employed does not make such corrections automatically.
Observe that the headers are different (Figure 30), depending on the type of notation selected. Also, note that the code for the modern notation includes, at the end, the command  [50] to generate the corresponding MIDI file.
[50] to generate the corresponding MIDI file.
8. Conclusions and Discussion
A complete OMR system for the analysis of manuscript music scores written in white mensural notation of the XVII-th and early XVIII-th centuries has been presented and two different notation styles have been considered. Multiple methods for the extraction of features of the music symbols are implemented and the resulting vectors are employed in several classification strategies.
User interaction has been limited to the selection of an initial ROI and the choice of some of the processing techniques available in the system at certain stages. Also, the calculation of the Hough transform used to correct the global rotation of the image, which is the process that takes longer computation time in the system implemented, can be replaced by the manual introduction of the rotation angle.
In the experiments, it has been observed that, in spite of the size of the database of scores used for training, the presence of some rare symbols had an important influence on the system. Some of the classification strategies have been adapted to use a reduced number of features in order to cope with these rare symbols in the same way as with the other common symbols. Hence, the methods that do not suffer from the scarceness of the reference elements are the ones that attain the best performance.
The best combination of techniques involves the usage of the k-NN method and the vectors of features based on the angular-radial transform (ART) coefficients. Success rates reach about  of symbols correctly recognized. Such performance is attained using a k-NN classifier that employs a large number of features (
of symbols correctly recognized. Such performance is attained using a k-NN classifier that employs a large number of features ( angular radial transform coefficients) that are able to represent, with high level of reliability, the very complex shape of the extracted symbols.
angular radial transform coefficients) that are able to represent, with high level of reliability, the very complex shape of the extracted symbols.
An open source program for music engraving (Lilypond) has been found useful to produce new scores from the ones processed using modern notation or white mensural notation, as in the original scores. Also, MIDI files could be automatically generated.
The trend for future developments of the system is mainly based on the improvement of the performance of the preprocessing steps. In fact, these stages are very important for the development of the OMR system. Also, a largest database of training data could allow to use more robustly some of the classification strategies evaluated, like the ones based on the Fisher linear discriminant, which are actually limited by the availability of samples of objects of certain rare classes.
References
Bainbridge D, Bell T: The challenge of optical music recognition. Computers and the Humanities 2001,35(2):95-121. 10.1023/A:1002485918032
Wolman J, Choi J, Asgharzadeh S, Kahana J: Recognition of handwritten music notation. Proceedings of the International Computer Music Conference, 1992, San Jose, Calif, USA 125-127.
McGee W, Merkley P: The optical scanning of medieval music. Computers and the Humanities 1991,25(1):47-53.
Carter NP: Segmentation and preliminary recognition of madrigals notated in white mensural notation. Machine Vision and Applications 1992,5(3):223-230. 10.1007/BF02627000
Pugin L, Burgoyne JA, Fujinaga I: Goal-directed evaluation for the improvement of optical music recognition on early music prints. Proceedings of the 7th ACM/IEEE Joint Conference on Digital Libraries (JCDL '07), June 2007, Vancouver, Canada 303-304.
Caldas Pinto J, Vieira P, Ramalho M, Mengucci M, Pina P, Muge F: Ancient music recovery for digital libraries. Proceedings of the 4th European Conference on Research and Advanced Technology for Digital Libraries, January 2000, Lecture Notes in Computer Science 24-34.
Fujinaga I: Adaptive optical music recognition, Ph.D. thesis. Faculty of Music, McGill University; June 1996.
Droetboom M, Fujinaga I, MacMillan K: Optical music interpretation. Proceedings of the IAPR International Workshop on Structural, Syntactic and Statistical Pattern Recognition, 2002, Lecture Notes in Computer Science 378-386.
Bainbridge D: Optical music recognition. In Progress Report. Department of Computer Science, University of Canterbury; 1994.
González RC, Woods RE: Digital Image Processing. Prentice-Hall, Upper Saddle River, NJ, USA; 2007.
Trabocchi O, Sanfilippo F: Efectos de la iluminación. Ingeniero en Automatización Y Control Industrial, Universidad Nacional de Quilmes; 2005.
Sanfilippo F, Trabocchi O: Tipos de iluminación. Ingeniero en Automatización Y Control Industrial, Universidad Nacional de Quilmes; 2005.
Otsu N: A threshold selection method from gray-level histograms. IEEE Transactions on Systems, Man and Cybernetics 1979,9(1):62-66.
Lu H, Cary PD: Deformation measurements by digital image correlation: implementation of a second-order displacement gradient. Experimental Mechanics 2000,40(4):393-400. 10.1007/BF02326485
Lobb R, Bell T, Bainbridge D: Fast capture of sheet music for an agile digital music library. Proceedings of the International Symposium on Music Information Retrieval, 2005 145-152.
Pitas I: Digital Image Processing Algorithms and Applications. Wiley-Interscience, New York, NY, USA; 2000.
Pratt WK: Digital Image Processing. John Wiley & Sons, New York, NY, USA; 2007.
Duda RO, Hart PE: Pattern Classification and Scene Analysis. John Wiley & Sons, New York, NY, USA; 1973.
Dalitz C, Droettboom M, Pranzas B, Fujinaga I: A comparative study of staff removal algorithms. IEEE Transactions on Pattern Analysis and Machine Intelligence 2008,30(5):753-766.
Szwoch M: A robust detector for distorted music staves. Proceedings of the 11th International Conference on Computer Analysis of Images and Patterns (CAIP '05), September 2005 3691: 701-708.
Therrien CW: Decision Estimation and Classification: An Introduction to Pattern Recognition and Related Topics. John Wiley & Sons, New York, NY, USA; 1989.
Lim JS: Two-Dimensional Signal and Image Processing. Prentice-Hall, Upper Saddle River, NJ, USA; 1990.
Blostein D, Baird HS: A critical survey of music image analysis. In Structured Document Image Analysis. Edited by: Baird HS, Bunke H, Yamamoto K. Springer, Berlin, Germany; 1992:405-434.
Pruslin D: Automatic recognition of sheet music, Ph.D. thesis. Massachusetts Institute of Technology, Cambridge, Mass, USA; June 1966.
Prerau DS: Computer pattern recognition of standard engraved music notation, Ph.D. thesis. Massachusetts Institute of Technology, Cambridge, Mass, USA; September 1970.
Andronico A, Ciampa A: On automatic pattern recognition and acquisition of printed music. Proceedings of the International Computer Music Conference (ICMC '82), 1982 245-278.
Mahoney JV: Automatic analysis of musical score images, M.S. thesis. Massachusetts Institute of Technology, Cambridge, Mass, USA; 1982.
Roach JW, Tatem JE: Using domain knowledge in low-level visual processing to interpret handwritten music: an experiment. Pattern Recognition 1988,21(1):33-44. 10.1016/0031-3203(88)90069-6
Carter NP: Automatic recognition of printed music in the context of electronic publishing, Ph.D. thesis. University of Surrey; February 1989.
Kato H, Inokuchi S: The recognition system of printed piano using musical knowledge and constraints. Proceedings of IAPR Workshop on Syntactic and Structured Pattern Recognition, June 1990 231-248.
Duda RO, Hart PE, Stork DG: Pattern Classification. Wiley-Interscience, New York, NY, USA; 2000.
Ng KC, Boyle RD: Recognition and reconstruction of primitives in music scores. Image and Vision Computing 1996,14(1):39-46. 10.1016/0262-8856(95)01038-6
Gezerlis VG, Theodoridis S: Optical character recognition of the Orthodox Hellenic Byzantine music notation. Pattern Recognition 2002,35(4):895-914. 10.1016/S0031-3203(01)00098-X
Theodoridis S, Koutroumbas K: Pattern Recognition. Academic Press, New York, NY, USA; 2006.
Llobet R, Pérez J, Paredes R: Técnicas reconocimiento de formas aplicadas al diagnóstico de cáncer asistido por ordenador. RevistaeSalud.com 2006.,2(7):
Sonka M, Havac V, Boyle R: Image Processing, Analysis and Machine Vision. Cambridge University Press, Cambridge, UK; 1993.
Zahn CT, Roskies RZ: Fourier descriptors for plane closed curves. IEEE Transactions on Computers 1972,21(3):269-281.
Christopoulos C, Skodras A, Ebrahimi T: The JPEG2000 still image coding system: an overview. IEEE Transactions on Consumer Electronics 2000,46(4):1103-1127. 10.1109/30.920468
Hwang S-K, Kim W-Y: Fast and efficient method for computing ART. IEEE Transactions on Image Processing 2006,15(1):112-117.
Höynck M, Ohm J-R: Shape retrieval with robustness against partial occlusion. Proceedings of the IEEE International Conference on Acoustics, Speech, and Signal Processing (ICASSP '03), April 2003, Hong Kong 3: 593-596.
De Maesschalck R, Jouan-Rimbaud D, Massart DL: Tutorial: the Mahalanobis distance. Chemometrics and Intelligent Laboratory Systems 2000, 50: 1-8. 10.1016/S0169-7439(99)00047-7
Stark H, Woods JW: Probability Random Processes & Estimation Theory for Engineers. Prentice-Hall, Upper Saddle River, NJ, USA; 1994.
Bainbridge D, Bell TC: Dealing with superimposed objects in optical music recognition. Proceedings of the 6th International Conference on Image Processing and Its Applications, July 1997, Dublin, Ireland 2: 756-760.
Good M: MusicXML for notation and analysis. In The Virtual Score: Representation, Retrieval, Restoration, Computing in Musicology, no. 12, Cambridge, Mass, USA. Edited by: Hewlett WB, Selfridge-Field E. MIT Press; 2001:113-124.
Bellini P, Nessi P: WEDELMUSIC format: and XML music notation format for emerging applications. Proceedings of the 1st International Conference on WEB Delivering of Music (WEDELMUSIC '01), 2001 79-86.
Hoos HH, Hamel KA, Reinz K, Kilian J: The GUIDO notation format. A novel approach for adequately representing score-level music. Proceedings of the International Computer Music Conference, 1998 451-454.
Bellini P, Nesi P, Zoia G: Symbolic music representation in MPEG. IEEE Multimedia 2005,12(4):42-49. 10.1109/MMUL.2005.82
LilyPond … music notation for everyone 2009, http://lilypond.org/web/index
Nienhuys H-W, Nieuwenhuizen J: Lilypond, a system for automated music engraving. Proceedings of the 14th Colloquium on Musical Informatis, 2003, Florence, Italy CIM-1-CIM-6.
Gnu lilypond—notation reference 2009, http://lilypond.org/doc/v2.12/Documentation/user/lilypond.pdf
Acknowledgments
This work has been funded by the Ministerio de Educatión y Ciencia of the Spanish Government under Project no. TSI2007-61181 and by the Junta de Andalucía under Project Number P07-TIC-02783. The authors are grateful to the person in charge of the Archivo de la Catedral de Málaga, who allowed the utilization of the data sets used in this work.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Tardón, L.J., Sammartino, S., Barbancho, I. et al. Optical Music Recognition for Scores Written in White Mensural Notation. J Image Video Proc 2009, 843401 (2009). https://doi.org/10.1155/2009/843401
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1155/2009/843401








 180° and
180° and 







 -projection) [
-projection) [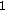 ).
).





 and the double whole (shaded areas in the staff).
and the double whole (shaded areas in the staff).
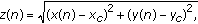
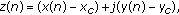



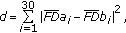
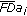 and
and 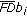 are the Fourier descriptors of the unknown symbol
are the Fourier descriptors of the unknown symbol  and the training one
and the training one 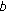 ,
,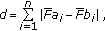
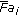 and
and 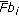 are the angular-radial transform coefficients (
are the angular-radial transform coefficients (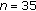 ), the wavelet transform coefficients (
), the wavelet transform coefficients (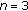 ) or the single parameter selected from the Fourier transform (
) or the single parameter selected from the Fourier transform (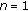 ), for the unknown element
), for the unknown element  and the training element
and the training element 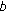 .
.



