- Research Article
- Open access
- Published:
Boosting Discriminant Learners for Gait Recognition Using MPCA Features
EURASIP Journal on Image and Video Processing volume 2009, Article number: 713183 (2009)
Abstract
This paper proposes a boosted linear discriminant analysis (LDA) solution on features extracted by the multilinear principal component analysis (MPCA) to enhance gait recognition performance. Three-dimensional gait objects are projected in the MPCA space first to obtain low-dimensional tensorial features. Then, lower-dimensional vectorial features are obtained through discriminative feature selection. These feature vectors are then fed into an LDA-style booster, where several regularized and weakened LDA learners work together to produce a strong learner through a novel feature weighting and sampling process. The LDA learner employs a simple nearest-neighbor classifier with a weighted angle distance measure for classification. The experimental results on the NIST/USF "Gait Challenge" data-sets show that the proposed solution has successfully improved the gait recognition performance and outperformed several state-of-the-art gait recognition algorithms.
1. Introduction
Automated human identification at a distance is important in visual surveillance and monitoring applications in security-sensitive environments such as airports, banks, shopping malls, parking lots, and large civic structures [1, 2]. However, many conventional biometrics, such as iris, face, and fingerprint, require the person to be recognized to be in close distance or even in contact with the capturing device. At a distance, these biometrics are usually not available in high enough resolution for recognition purposes.
Gait, the style of walking of an individual, is an emerging behavioral biometric that offers the potential for vision-based recognition at a distance [3–6]. In 1975 [7], Johansson used point light displays to show humans' ability to distinguish human locomotion from other motion patterns. Later, experiments demonstrate the capability of identifying familiar individuals or the gender of a person [8, 9]. Nonetheless, researches on gait recognition from video sequences are only receiving significant attentions recently. Vision-based gait recognition is particularly attractive in human identification at a distance because gait capture is unobtrusive, requiring no cooperation or attention of the observed subject, and gait is difficult to hide [5, 10].
There are two approaches to gait recognition: the model-based approach [11–13], where human body structure is explicitly modeled, and the appearance-based approach [5, 6, 10, 14–18], where gait is treated as a sequence of holistic binary patterns (silhouettes). It should be noted that although the EigenGait approach [18] makes use of silhouettes as well, a motion-based recognition approach is taken where features are extracted from the image self-similarity plots rather than from the silhouettes directly. The appearance-based approach has been more successful working on practical data [10]. Appearance-based approaches take binary gait silhouette sequences extracted from raw gait sequences [19–21] as the input. These gait silhouette sequences are naturally three-dimensional objects, also called third-order tensors, and the three dimensions are the spatial row, column, and the temporal modes [22]. These tensor objects are in a very high-dimensional tensor space. To apply traditional linear feature extraction algorithms such as the Principal Component Analysis (PCA) and Linear Discriminant Analysis (LDA) on these tensorial data, they need to be first reshaped (vectorized) into vectors in a very high dimensional space. This reshaping does not only result in high computation and memory demand but also breaks the structure and correlation in the original data. This problem has motivated the development of multilinear subspace learning algorithms operating directly on the gait sequences in their tensorial representation rather than their vectorized forms. In particular, the multilinear PCA (MPCA) algorithm [22] aims to determine a multilinear projection that projects the original tensor objects into a lower-dimensional tensor subspace while preserving the variation in the original data as much as possible. For gait recognition, a number of discriminative features in the projected tensor space can be selected. The MPCA-based gait recognition algorithm has achieved better overall performance when compared with the state-of-the-art gait recognition algorithms.
Although progresses have been made in gait recognition, it remains a very challenging problem. A person's gait can be affected by many factors, such as viewing angles, walking surfaces and shoes. Similar to face patterns, the distribution of gait patterns is expected to be nonlinear and complex. Furthermore, the gait data in training and those in testing may be captured under different conditions and this makes generalization very difficult, as studied in the Gait Challenge problem [10]. There are many methods proposed in literature to handle complex and nonlinear patterns. The ensemble-based machine-learning method named boosting is a very promising one that offers good generalization capability. Traditional boosting design works through the combination of a set of weak classifiers repeatedly trained on weighted training samples [23, 24], which tends to be an adaptive feature-selection process [25]. Feature extraction is not a concern in these boosters and the requirement of an appropriate weak learner in boosting has restricted its applicability [24, 26]. A recent work in [27] has broken this limitation by proposing a boosting algorithm that puts the learning focus on the feature extractor rather than the classifier so that the new boosting scheme works with LDA-style learners. The effectiveness of the boosting scheme proposed in [27] has been demonstrated on the problem of face recognition. A cross-validation mechanism is employed to weaken the LDA learner, and the pairwise class discriminant distribution (PCDD) is introduced for interaction between the booster and the learner.
In this paper, the boosting work in [27] is enhanced and extended so it can be successfully applied to the problem of gait recognition through combination with the recent development of MPCA [22]. It should be noted that, to the best of the authors' knowledge, this is the first work that has applied boosting to gait recognition although boosting has been well studied for face recognition [27–29]. In the proposed processing scheme, MPCA [22] first produces EigenTensorGaits (ETGs) in a lower-dimensional tensor space and then only a number of discriminative ETGs are selected as the input to the LDA-based booster. There are two main advantages in this scheme. On one hand, the MPCA feature extractor applied before the booster reduces the processing cost greatly (in both training and testing) such that the very-high-dimensional tensorial gait data can be handled efficiently. On the other hand, the number of selected ETGs provides another way (in addition to the cross-validation mechanism in [27]) to control the weakness of the LDA learner. In addition, in order to improve the generalization performance further, a regularization mechanism is incorporated since the within-class scatter of gait patterns under the capturing conditions in testing is expected to be larger than that of gait patterns in training. Furthermore, the training sample selection scheme in the original LDA-style boosting scheme proposed in [27] tends to prevent the inclusion of "difficult" (hard to classify correctly) samples in subsequent boosting steps. Therefore, a new training sample selection method is introduced in this paper to include more "difficult" samples in subsequent boosting steps to get better boosting results.
The rest of the paper is organized as follows. Section 2 briefly reviews the MPCA-based gait feature extraction method introduced in [22]. Section 3 proposes the LDA-based boosting algorithm operating on MPCA features for enhancing gait recognition performance. In Section 4, experimental results on the NIST/USF "Gait Challenge" datasets are presented and the proposed algorithm is compared with the state-of-the-art gait recognition algorithms to illustrate the effectiveness of the proposed solution. Finally, conclusions are drawn in Section 5.
2. Review of MPCA-Based Gait Feature Extraction
MPCA [22] is a multilinear subspace learning method that extracts features directly from tensorial representation of multidimensional objects. In this section, the notations are introduced and the MPCA-based gait feature extraction algorithm is briefly reviewed.
2.1. Notations
In this paper, vectors are denoted by lowercase boldface letters, for example,  ; matrices by uppercase boldface, for example,
; matrices by uppercase boldface, for example,  ; tensors by calligraphic letters, for example,
; tensors by calligraphic letters, for example,  . Their elements are denoted with indices in brackets. Indices are denoted by lowercase letters and span the range from 1 to the uppercase letter of the index, for example,
. Their elements are denoted with indices in brackets. Indices are denoted by lowercase letters and span the range from 1 to the uppercase letter of the index, for example,  . An
. An  th-order tensor is denoted as
th-order tensor is denoted as  . It is addressed by
. It is addressed by  indices
indices  ,
,  , and each
, and each  addresses the
addresses the  -mode of
-mode of  . The
. The  -mode product of a tensor
-mode product of a tensor  by a matrix
by a matrix  , denoted by
, denoted by  , is a tensor with entries [30–32]:
, is a tensor with entries [30–32]:

A rank- tensor
tensor  equals the outer product of
equals the outer product of  vectors:
vectors:

which means that

for all values of indices [22, 30, 32].
2.2. Gait Feature Extraction through MPCA
In the MPCA-based gait feature extraction algorithm proposed in [22], a gait sample is a half cycle of gait silhouette sequences, represented naturally as a third-order tensor. The procedures described in [22] are followed to obtain these gait samples, where the foreground pixels in the lower-half of the silhouettes are counted and the minimums of the foreground pixel number sequence partition a gait sequence into half cycles. Another choice is to use full cycles as gait samples, which results in larger sample size in the time mode but fewer samples available for both training and test, while asymmetry between two adjacent half cycles could be potentially useful for discrimination in this case. In addition, half cycles may not always be an appropriate choice for gait samples. For example, when a luggage is carried on one side, full cycles are more appropriate to be used as gait samples. Thus, it will be worthwhile to study the effects of this choice on the gait recognition performance. However, this issue is out of the scope of this paper and it is left for future works since this paper focuses on the incorporation of the boosting scheme in gait recognition. There are two types of gait datasets in a typical gait recognition problem: the gallery and the probe [10]. Gait samples in the gallery set are labeled with their identities and they are used as training data, while the probe set contains the test data, which are gait samples of unknown identities that need to be matched against those included in the gallery set.
The input to MPCA are third-order gallery gait samples  , …,
, …,  , where
, where  is the total number of gait samples in the gallery set. The MPCA algorithm solves for a multilinear transformation
is the total number of gait samples in the gallery set. The MPCA algorithm solves for a multilinear transformation

where  for
for  , that maps the original gait tensor space
, that maps the original gait tensor space  into a lower-dimensional tensor subspace
into a lower-dimensional tensor subspace  :
:

such that the total tensor scatter

is maximized, where  is the average of the training samples [22], that is, the mean sample. This MPCA problem is solved through an iterative alternating projection method in [22].
is the average of the training samples [22], that is, the mean sample. This MPCA problem is solved through an iterative alternating projection method in [22].
The MPCA projection matrices  can be viewed as
can be viewed as  so-called EigenTensorGaits (ETGs) [22]:
so-called EigenTensorGaits (ETGs) [22]:

where  is the
is the  column of
column of  . Since MPCA is unsupervised and the class information is not considered in feature extraction, not all ETGs are useful for recognition purposes. Therefore, in [22], a number of discriminative ETGs are selected according to their class discriminability
. Since MPCA is unsupervised and the class information is not considered in feature extraction, not all ETGs are useful for recognition purposes. Therefore, in [22], a number of discriminative ETGs are selected according to their class discriminability  , where
, where  for the eigentensor
for the eigentensor  is defined as
is defined as

where  denotes the number of classes (subjects),
denotes the number of classes (subjects),  denotes the number of gait samples for class (subject)
denotes the number of gait samples for class (subject)  , and
, and  denotes the class label for the
denotes the class label for the  th gallery gait sample
th gallery gait sample  . Also,
. Also,  is the feature tensor of
is the feature tensor of  in the projected MPCA subspace, the mean feature tensor
in the projected MPCA subspace, the mean feature tensor  and the class mean feature tensor
and the class mean feature tensor  . For the ETG selection, the entries in
. For the ETG selection, the entries in  are arranged into a feature vector
are arranged into a feature vector  according to
according to  in descending order. Only the first
in descending order. Only the first  entries of
entries of  are kept for subsequent recognition task [22]. It should be noted that discriminability is only considered in the ETG selection process, while the selected ETG features are extracted in an unsupervised way by MPCA.
are kept for subsequent recognition task [22]. It should be noted that discriminability is only considered in the ETG selection process, while the selected ETG features are extracted in an unsupervised way by MPCA.
3. Boosting LDA-Style Learners on MPCA Features for Gait Recognition
Figure 1 illustrates the proposed new gait recognition method. Input tensorial gait samples are projected through MPCA and a number of discriminative EigenTensorGaits (ETGs) are selected to obtain gait feature vectors as in [22]. The extracted discriminative feature vectors are then fed into a new LDA-based booster built upon the booster in [27] for learning and classification. This section presents the proposed LDA-based booster in detail.
3.1. The Boosting Scheme
The pseudocode implementation of the proposed MPCA+boosting scheme is summarized in Algorithm 1. As in [27], the AdaBoost.M2 algorithm [23] is followed here. AdaBoost.M2 aims to extend the communication between the boosting algorithm and the weak learner by allowing the weak learner to generate more expressive hypotheses (a set of "plausible" labels rather than a single label) indicating a "degree of plausibility", that is, a hypothesis  takes a sample
takes a sample  and a class label
and a class label  as the inputs and produces a "plausibility" score
as the inputs and produces a "plausibility" score  as the output. To achieve its objective, the AdaBoost.M2 introduces a sophisticated error measure pseudoloss
as the output. To achieve its objective, the AdaBoost.M2 introduces a sophisticated error measure pseudoloss  with respect to the mislabel distribution
with respect to the mislabel distribution  in [23]. Thus,
in [23]. Thus,  is an
is an  matrix. A mislabel is a pair
matrix. A mislabel is a pair  , where
, where  is the index of a training sample and
is the index of a training sample and  is an incorrect label associated with the sample
is an incorrect label associated with the sample  . Let
. Let  be the set of all mislabels:
be the set of all mislabels:

The mislabel distribution is initialized as

for  . Accordingly, the weak learner produces a hypothesis:
. Accordingly, the weak learner produces a hypothesis:

where  measures the degree to which it is believed that
measures the degree to which it is believed that  is the correct label for
is the correct label for  . The pseudoloss
. The pseudoloss  of the hypothesis
of the hypothesis  with respect to
with respect to  is defined to measure the goodness of
is defined to measure the goodness of  and it is given by [23]
and it is given by [23]

The introduction of the mislabel distribution enhances the communication between the learner and the booster, so that the AdaBoost.M2 can focus the weak learner not only on hard-to-classify samples but also on the incorrect labels that are the hardest to discriminate [23].
Algorithm 1: The pseudocode implementation of the LDA-based booster.
Inpout: The gallery gait feature vectors  with class labels
with class labels  , the LDA
, the LDA
learner described in Section 3.2, the number of samples for LDA training  , the maximum
, the maximum
number of iterations  .
.
Algorithm:
-
(i)
Initialize
 ,
, 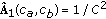 ,
, 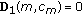 ,
,  ,
,and
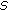 samples are selected to form the initial training set
samples are selected to form the initial training set 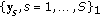 ,
,with the first
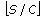 or
or 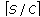 samples from each class, where
samples from each class, where  and
and  are
arethe floor and ceil functions, respectively.
-
(ii)
Do for
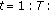
-
(
 ) Get
) Get 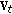 from
from 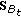 and
and  constructed from
constructed from 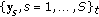 and project
and project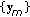 to
to  .
.(
 ) Get hypothesis
) Get hypothesis 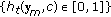 by applying the nearest neighbor classi-
by applying the nearest neighbor classi-fier with the MAD measure [22] on
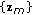 .
.(
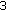 ) Calculate
) Calculate 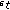 , the pseudo-loss of
, the pseudo-loss of 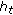 , from (12).
, from (12).(
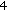 ) Set
) Set 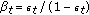 .
.(
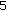 ) Update
) Update 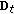 :
: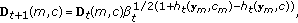
and normalize it:
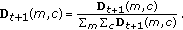
(
 ) Update
) Update 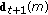 ,
, 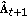 and
and 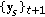 accordingly.
accordingly.
Output: The final hypothesis:

-
Another distribution  , named as pseudosample distribution in [27], is derived from
, named as pseudosample distribution in [27], is derived from  as
as

Thus,  is an
is an  vector.
vector.
For the communication between the booster and the learner, the following "pairwise class discriminant distribution" (PCDD)  was introduced in [27]
was introduced in [27]

where

and the diagonal of  is set to zeros.
is set to zeros.
3.2. The LDA Learner
In building the LDA learner, the approach in [27] is adopted with several enhancement.
( ) In [27],
) In [27],  samples per class are used as the input to the LDA learner in order to get weaker but more diverse LDA learners;
samples per class are used as the input to the LDA learner in order to get weaker but more diverse LDA learners;  random samples per class are taken for the first boosting step; the hardest
random samples per class are taken for the first boosting step; the hardest  (with the largest
(with the largest  ) samples per class are selected for subsequent steps. Let
) samples per class are selected for subsequent steps. Let  denote the selected samples, where
denote the selected samples, where  for the sample selection scheme in [27].
for the sample selection scheme in [27].
This sample selection scheme has a problem that is against the design principal of boosting, where the hardest samples should be selected for subsequent learning. Figure 8(a) gives a typical example of the average weights of the samples selected according to the method in [27], denoted as "Old selection." From the figure, the hardness of the selected samples (i.e., the weight) decreases quickly after the first few boosting steps. The reason is that it is not true in most cases that the hardest samples will be distributed evenly among all the classes. In fact, it is common that some classes have more hard samples while some classes have more easy samples. Therefore, in this paper, a new sample selection scheme is proposed to enhance the sample selection process in boosting, described as follows.
-
(a)
For each class, select the hardest sample to result in
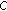 samples added to the pool of training sample for subsequent learning.
samples added to the pool of training sample for subsequent learning. -
(b)
Select the hardest
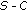 samples among all the rest samples, regardless of their class labels so that together with the
samples among all the rest samples, regardless of their class labels so that together with the  samples selected in the previous step,
samples selected in the previous step, 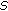 samples are chosen for subsequent boosting.
samples are chosen for subsequent boosting.
The average weights of the samples selected according to the sample selection scheme proposed above are shown in Figure 8(a) as well, denoted as "New selection." As seen from the figure, the new sample selection scheme results in samples with much larger weights selected compared to the scheme in [27].
( ) For the between-class scatter matrix
) For the between-class scatter matrix  , the pairwise between-class scatter in [33] is used instead of that used in [27] in this paper for its simplicity and easy computation:
, the pairwise between-class scatter in [33] is used instead of that used in [27] in this paper for its simplicity and easy computation:

where

is the mean for class  .
.
( ) For the within-class scatter matrix, a regularized version of that in [27] is used:
) For the within-class scatter matrix, a regularized version of that in [27] is used:

where  is a regularization parameter to increase the estimated within-class scatter and
is a regularization parameter to increase the estimated within-class scatter and  is an identity matrix of size
is an identity matrix of size  . The regularization term is added because in the gait recognition problem, the actual within-class scatter of gait sequences captured under various conditions is expected to be greater than the within-class scatter that can be estimated from the gallery set, which is captured under a single condition.
. The regularization term is added because in the gait recognition problem, the actual within-class scatter of gait sequences captured under various conditions is expected to be greater than the within-class scatter that can be estimated from the gallery set, which is captured under a single condition.
With these definitions, the projection  is then to be solved to maximize the ratio of the between-class scatter to the within-class scatter. The solution is
is then to be solved to maximize the ratio of the between-class scatter to the within-class scatter. The solution is

where  is the set of generalized eigenvalues of
is the set of generalized eigenvalues of  and
and  corresponding to the
corresponding to the  (
( ) largest generalized eigenvalues
) largest generalized eigenvalues  :
:

Thus, the LDA feature vector  is obtained as
is obtained as  for the input to a classifier.
for the input to a classifier.
The nearest neighbor classifier (NNC), which assigns label  to the test sample
to the test sample  if
if  is the class label of the sample nearest to
is the class label of the sample nearest to  , is used with the modified angle distance (MAD) measure defined in [22], which is found to have the best performance for MPCA-based algorithms in gait recognition. The MAD between two feature vectors
, is used with the modified angle distance (MAD) measure defined in [22], which is found to have the best performance for MPCA-based algorithms in gait recognition. The MAD between two feature vectors  and
and  is calculated as
is calculated as

The calculated distances between a sample and the  class means are matched to the interval
class means are matched to the interval  as required by the AdaBoost.M2 algorithm.
as required by the AdaBoost.M2 algorithm.
3.3. Discussions
It should be noted that beside the algorithmic difference, the proposed solution has an important difference in design with that in [27]. Direct application of the algorithm in [27] on the gait recognition problem requires the vectorization of the tensorial input  to
to  . For a gait sample of typical size
. For a gait sample of typical size  , the resulted vectors are of size
, the resulted vectors are of size  . In contrast, the LDA-based learners in the proposed booster take the gait feature vectors extracted by MPCA
. In contrast, the LDA-based learners in the proposed booster take the gait feature vectors extracted by MPCA  , rather than the original data
, rather than the original data  . The proposed scheme has two benefits.
. The proposed scheme has two benefits.
( ) The number of selected discriminative ETGs, which is the gait feature vector dimension
) The number of selected discriminative ETGs, which is the gait feature vector dimension  , gives us one more degree (besides the number of samples used for LDA learners) to control the weakness of the LDA learners. Similar to the case of PCA+LDA, where the recognition performance is often affected by the number of principal components for input to LDA,
, gives us one more degree (besides the number of samples used for LDA learners) to control the weakness of the LDA learners. Similar to the case of PCA+LDA, where the recognition performance is often affected by the number of principal components for input to LDA,  affects the recognition performance of LDA on the MPCA features as well, as observed in [22]. Therefore, by choosing a value of
affects the recognition performance of LDA on the MPCA features as well, as observed in [22]. Therefore, by choosing a value of  that is not optimal for a single LDA learner, the obtained LDA learner is weakened. On the other hand, the LDA learner cannot be made "too weak" either. Otherwise, the boosting scheme will not work.
that is not optimal for a single LDA learner, the obtained LDA learner is weakened. On the other hand, the LDA learner cannot be made "too weak" either. Otherwise, the boosting scheme will not work.
( ) Using feature vectors of dimensionality
) Using feature vectors of dimensionality  instead of the original high-dimensional data as the booster input is computationally advantageous. Since boosting is an iterative algorithm with
instead of the original high-dimensional data as the booster input is computationally advantageous. Since boosting is an iterative algorithm with  rounds, the computational cost is about
rounds, the computational cost is about  times of that of a single learner with the same input, both in training and testing. When the booster works on lower-dimensional features extracted by MPCA, it becomes much more efficient since it needs to deal with low-dimensional vectors only in each round. For instance, the dimension of the input vectors to the booster is around
times of that of a single learner with the same input, both in training and testing. When the booster works on lower-dimensional features extracted by MPCA, it becomes much more efficient since it needs to deal with low-dimensional vectors only in each round. For instance, the dimension of the input vectors to the booster is around  in this paper, which is much smaller than the dimension
in this paper, which is much smaller than the dimension  for face data in [27] and the original gait data dimension
for face data in [27] and the original gait data dimension  . Therefore, the computational cost is reduced significantly this way.
. Therefore, the computational cost is reduced significantly this way.
4. Experimental Results
This section evaluates the proposed solution of LDA-based boosting on MPCA features (B-LDA-MPCA) through the following studies:
-
(1)
the comparison of gait recognition performance against the state-of-the-art gait recognition algorithms,
-
(2)
the effects of the gait feature vector dimension
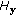 for input to LDA learners, the LDA feature vector dimension
for input to LDA learners, the LDA feature vector dimension 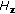 , the number of LDA training samples for LDA learner input
, the number of LDA training samples for LDA learner input  , and the regularization parameter
, and the regularization parameter  on boosting recognition performance,
on boosting recognition performance, -
(3)
the effectiveness of the new sample selection scheme proposed in this paper in improving the booster performance.
4.1. The Datasets
The NIST/USF "Gait Challenge" datasets version 1.7 [10, 34] is chosen to carry out the gait recognition experiments. All the recognition results reported and compared in this paper are obtained from this database. It consists of  sequences from
sequences from  subjects walking in elliptical paths in front of the camera, with two viewpoints (left or right), two shoe types (A or B) and two surface types (grass or concrete). There is a newer version 2.1 available, which is of much larger size with two additional differences in briefcase carrying condition and time (including clothing). Version 1.7 is chosen in this work because this version is widely used in the research community as well and the performance on it is far from saturated [4, 5, 14, 16, 17, 22]. In addition, version 1.7 is much smaller than version 2.1 so the computational demand is much lower in experimental evaluation.
subjects walking in elliptical paths in front of the camera, with two viewpoints (left or right), two shoe types (A or B) and two surface types (grass or concrete). There is a newer version 2.1 available, which is of much larger size with two additional differences in briefcase carrying condition and time (including clothing). Version 1.7 is chosen in this work because this version is widely used in the research community as well and the performance on it is far from saturated [4, 5, 14, 16, 17, 22]. In addition, version 1.7 is much smaller than version 2.1 so the computational demand is much lower in experimental evaluation.
The gallery set contains 71 sequences (one sequence from each subject). Seven experiments, corresponding to seven probe sets, are designed for human identification. Subjects are unique in the gallery and each probe set. There are no common sequences between the gallery set and any of the probe sets. Also, all the probe sets are distinct. The number of sequences in each probe set and the difference from the gallery set are summarized in Table 1. The capturing condition for each probe set is indicated in brackets after the probe name, where C, G, A, B, L, R, stand for cement surface, grass surface, shoe type A, shoe type B, left view, and right view, respectively.
The procedures described in [22] are used to obtain the third-order tensorial gait samples  of size
of size  , with five examples shown as unfolded images in Figure 2. There are 731 gait samples in the Gallery set and each subject has an average of roughly
, with five examples shown as unfolded images in Figure 2. There are 731 gait samples in the Gallery set and each subject has an average of roughly  samples available. MPCA is applied to get the gait feature vectors
samples available. MPCA is applied to get the gait feature vectors  for the input to the booster. The rank 1 and rank 5 identification rates are used for recognition performance evaluation, where rank
for the input to the booster. The rank 1 and rank 5 identification rates are used for recognition performance evaluation, where rank  results report the percentage of probe subjects whose true match in the gallery set was in the top
results report the percentage of probe subjects whose true match in the gallery set was in the top  matches [10].
matches [10].
4.2. Comparison of Gait Recognition Results with the State-of-the-Art Algorithms
There are several parameters in the proposed B-LDA-MPCA solution:  ,
,  ,
,  ,
,  and
and  . As in other boosting algorithms [27], the optimal determination of these parameters is still an open problem to be solved. The maximum number of iterations is set to
. As in other boosting algorithms [27], the optimal determination of these parameters is still an open problem to be solved. The maximum number of iterations is set to  , as in [27]. Several values of the other four parameters are tested empirically, listed as follows:
, as in [27]. Several values of the other four parameters are tested empirically, listed as follows:
-
(i)
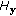 :
:  ,
,  ,
, 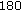 ,
,  ,
, 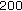 ,
, 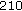 ,
, 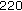 .
. -
(ii)
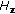 :
: 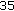 ,
, 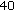 ,
, 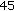 ,
,  ,
, 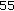 ,
, 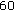 ,
,  ,
, 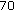 .
. -
(iii)
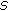 :
: 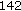 ,
, 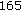 ,
,  ,
, 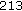 ,
, 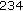 ,
,  ,
,  .
. -
(iv)
 :
: 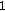 ,
, 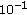 ,
,  ,
,  ,
,  .
.
For the proposed B-LDA-MPCA algorithm, the parameters producing the highest rank-1 identification rates averaged over all seven probes in the test are  ,
,  ,
,  , and
, and  , which are considered to be the best performing set of parameters in this paper. The evolutions of various identification rates over the boosting steps are shown in Figure 3 with this set of parameters. In the figure legends, "R1" and "R5" stand for the average rank 1 and rank 5 identification rates, respectively. The identification rate obtained from the single learner in each step is denoted as "Sgl" and that obtained from the aggregated learners is denoted by "Bst." From the figure, the effectiveness of the boosting scheme is observed. There are about
, which are considered to be the best performing set of parameters in this paper. The evolutions of various identification rates over the boosting steps are shown in Figure 3 with this set of parameters. In the figure legends, "R1" and "R5" stand for the average rank 1 and rank 5 identification rates, respectively. The identification rate obtained from the single learner in each step is denoted as "Sgl" and that obtained from the aggregated learners is denoted by "Bst." From the figure, the effectiveness of the boosting scheme is observed. There are about  boost in both rank 1 and rank 5 identification rates through the combination of single learners.
boost in both rank 1 and rank 5 identification rates through the combination of single learners.
Tables 2 and 3 show the detailed rank 1 and rank 5 gait recognition results, respectively, of B-LDA-MPCA on each probe set, obtained with the best parameter settings tested. In addition, the tables also include the results from the baseline algorithm [10, 34] as well as the following state-of-the-art gait recognition algorithms: the Hidden Markov Model (HMM) framework [4], the linear time normalization (LTN) algorithm [16], the Gait Energy Image (GEI) algorithm [17], and the MPCA+LDA algorithm [22]. The average identification rates over the seven probes are also shown for comparison of the overall performance. The best results for each column are highlighted by boldface font in the tables.
From the results, the B-LDA-MPCA algorithm has achieved the best rank 1 and rank 5 recognition results on all probes except the rank 1 identification rate on probe B and the rank 5 identification rate on probe D, demonstrating its superior recognition performance. Compared to the MPCA+LDA algorithm, the B-LDA-MPCA algorithm has improved the rank 1 identification rate by an average of  and the rank 5 identification rate by an average of
and the rank 5 identification rate by an average of  . The greatest improvement in rank 1 identification rate is
. The greatest improvement in rank 1 identification rate is  on probe F, and the greatest improvement in rank 5 identification rate is
on probe F, and the greatest improvement in rank 5 identification rate is  on probe E. In particular, in rank 1 identification rates, the performance improvement on the more difficult probes, D, E, F, and G, are more significant than the improvement on the easier probes, A, B, and C, showing that the B-LDA-MPCA algorithm indeed generalizes better than the MPCA+LDA algorithm.
on probe E. In particular, in rank 1 identification rates, the performance improvement on the more difficult probes, D, E, F, and G, are more significant than the improvement on the easier probes, A, B, and C, showing that the B-LDA-MPCA algorithm indeed generalizes better than the MPCA+LDA algorithm.
4.3. The Effects of 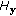 ,
,  ,
, 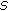 , and
, and  on Boosting
on Boosting
The effects of  ,
,  ,
,  and
and  on the average rank 1 and rank 5 gait recognition performance of the proposed method are shown in Figures 4, 5, 6, and 7, respectively. The effects of a parameter are shown by varying only the parameter of interest while fixing all the other parameters since it is not possible to show the results of all possible parameter combinations. Only a number of values are tested for each parameter, as specified in Section 4.2. The fixed set of parameters is chosen to be the best set described in Section 4.2.
on the average rank 1 and rank 5 gait recognition performance of the proposed method are shown in Figures 4, 5, 6, and 7, respectively. The effects of a parameter are shown by varying only the parameter of interest while fixing all the other parameters since it is not possible to show the results of all possible parameter combinations. Only a number of values are tested for each parameter, as specified in Section 4.2. The fixed set of parameters is chosen to be the best set described in Section 4.2.
Comparison of the proposed sample selection scheme against the sample selection scheme in [27]. The average weights of selected samplesRank 1 identification rateRank 5 identification rate
The proposed method introduces an additional learner weakness control mechanism by  . From [22],
. From [22],  gives the best gait recognition performance with the MAD measure and the NNC classifier. From Figure 4, the weaker learners with
gives the best gait recognition performance with the MAD measure and the NNC classifier. From Figure 4, the weaker learners with  give much better boosting results than the stronger learners with
give much better boosting results than the stronger learners with  . This confirms that
. This confirms that  can improve the boosting performance through controlling the weakness of the learners.
can improve the boosting performance through controlling the weakness of the learners.
The dimensionality of the LDA features  affects the recognition performance of the proposed solution as well. Since
affects the recognition performance of the proposed solution as well. Since  , the maximum dimensionality of the features extracted by LDA learners is
, the maximum dimensionality of the features extracted by LDA learners is  . Nonetheless, as pointed out in [27], if
. Nonetheless, as pointed out in [27], if  , the resulted LDA learner will be very strong, deteriorating the performance of the booster. From Figure 5, it can be seen that the value of
, the resulted LDA learner will be very strong, deteriorating the performance of the booster. From Figure 5, it can be seen that the value of  giving the best performance is a medium value. It is also evident from the figure that the strong learner with
giving the best performance is a medium value. It is also evident from the figure that the strong learner with  collapsed around the
collapsed around the  th boosting step, as expected in boosting [27]. This set of experiments demonstrate that appropriate weakness is again required and the best boosting performance cannot be reached with too strong or too weak learners.
th boosting step, as expected in boosting [27]. This set of experiments demonstrate that appropriate weakness is again required and the best boosting performance cannot be reached with too strong or too weak learners.
The value of  determines the number of training samples for the LDA learners. As discussed in [27], the diversity of the LDA learners is necessary to ensure good boosting performance. Therefore, by choosing only a subset of the available training samples, the diversity among learners at different boosting steps is enhanced. On the other hand,
determines the number of training samples for the LDA learners. As discussed in [27], the diversity of the LDA learners is necessary to ensure good boosting performance. Therefore, by choosing only a subset of the available training samples, the diversity among learners at different boosting steps is enhanced. On the other hand,  needs to be sufficiently large to enable learners to achieve a certain classification accuracy. Figure 6 illustrates the effects of
needs to be sufficiently large to enable learners to achieve a certain classification accuracy. Figure 6 illustrates the effects of  discussed here, showing that an appropriate choice of
discussed here, showing that an appropriate choice of  is neither too small nor too large.
is neither too small nor too large.
The effects of regularization are depicted in Figure 7, where it is shown that an appropriate regularization parameter  does result in better generalization. This study confirms that gait recognizer can benefit from making use of the fact that the within-class scatter of gait patterns under various capturing conditions is greater than that under the same capturing condition.
does result in better generalization. This study confirms that gait recognizer can benefit from making use of the fact that the within-class scatter of gait patterns under various capturing conditions is greater than that under the same capturing condition.
4.4. The Effectiveness of the Proposed Sample Selection Scheme for LDA Learners in Boosting the Recognition Performance
Figure 8 demonstrates the effectiveness of the new sample selection scheme proposed in Section 3.2. As discussed in Section 3.2 and illustrated in Figure 8(a), the proposed scheme selects samples with much larger weights for subsequent boosting steps, compared with the scheme in [27]. Thus, the new scheme focuses more on the difficult samples, which agrees with the working principle behind boosting. The effects of the new sample selection scheme on the recognition performance are shown in Figures 8(b) and 8(c), where the corresponding average rank 1 and rank 5 identification rates are compared, respectively. From the figure, it can be seen that the proposed new sample selection scheme results in approximately  improvement in both rank 1 and rank 5 identification rates.
improvement in both rank 1 and rank 5 identification rates.
5. Conclusions
This paper proposes a gait recognition solution through combining the MPCA algorithm [22] and the ensemble-based discriminant learning method in [27]. The MPCA algorithm in [22] is used to extract features from tensorial gait data and a subset of the extracted features are fed into an enhanced LDA-style booster. This scheme gives another way of learner weakness control in addition to computational efficiency. The LDA learner in [27] is modified by adopting a simpler weighted pairwise between-class scatter matrix and introducing a regularization term in the within-class scatter matrix so that the gait challenge due to various capturing conditions is taken into account. Furthermore, a new sample selection scheme of the LDA-based booster is proposed to concentrate more on the "difficult" samples in the boosting process. Experiments carried out on the gait challenge datasets show that the proposed scheme is effective in boosting the gait recognition performance and outperforms several state-of-the-art gait recognition algorithms.
References
Jain AK, Ross A, Prabhakar S: An introduction to biometric recognition. IEEE Transactions on Circuits and Systems for Video Technology 2004,14(1):4-20. 10.1109/TCSVT.2003.818349
Lu H, Wang J, Plataniotis KN: A review on face and gait recognition: system, data and algorithms. In Advanced Signal Processing: Theory and Implementation for Sonar, Radar, and Non-Invasive Medical Diagnostic Systems. 2nd edition. Edited by: Stergiopoulos S. CRC Press, Boca Raton, Fla, USA; 2009:303-330.
Nixon MS, Carter JN: Automatic recognition by gait. Proceedings of the IEEE 2006,94(11):2013-2024.
Kale A, Sundaresan A, Rajagopalan AN, et al.: Identification of humans using gait. IEEE Transactions on Image Processing 2004,13(9):1163-1173. 10.1109/TIP.2004.832865
Boulgouris NV, Hatzinakos D, Plataniotis KN: Gait recognition: a challenging signal processing technology for biometrics. IEEE Signal Processing Magazine 2005,22(6):78-90.
Wang L, Tan T, Ning H, Hu W: Silhouette analysis-based gait recognition for human identification. IEEE Transactions on Pattern Analysis and Machine Intelligence 2003,25(12):1505-1518. 10.1109/TPAMI.2003.1251144
Johansson G: Visual motion perception. Scientific American 1975,232(6):76-88. 10.1038/scientificamerican0675-76
Cutting J, Kozlowski L: Recognizing friends by their walk: gait perception without familiarity cues. Bulletin of the Psychonomic Society 1977,9(5):353-356.
Barclay CD, Cutting JE, Kozlowski LT: Temporal and spatial factors in gait perception that influence gender recognition. Perception and Psychophysics 1978,23(2):145-152. 10.3758/BF03208295
Sarkar S, Phillips PJ, Liu Z, Robledo I, Grother P, Bowyer KW: The human ID gait challenge problem: data sets, performance, and analysis. IEEE Transactions on Pattern Analysis and Machine Intelligence 2005,27(2):162-177.
Lu H, Plataniotis KN, Venetsanopoulos AN: A layered deformable model for gait analysis. Proceedings of the 7th International Conference on Automatic Face and Gesture Recognition (FGR '06), April 2006 249-256.
Yam CY, Nixon MS, Carter JN: Automated person recognition by walking and running via model-based approaches. Pattern Recognition 2004,37(5):1057-1072. 10.1016/j.patcog.2003.09.012
Lu H, Plataniotis KN, Venetsanopoulos AN: A full-body layered deformable model for automatic model-based gait recognition. EURASIP Journal on Advances in Signal Processing 2008, 2008:-13.
Lu H, Plataniotis KN, Venetsanopoulos AN: Uncorrelated multilinear discriminant analysis with regularization and aggregation for tensor object recognition. IEEE Transactions on Neural Networks 2009,20(1):103-123.
Lu H, Plataniotis KN, Venetsanopoulos AN: Multilinear principal component analysis of tensor objects for recognition. Proceedings of the International Conference on Pattern Recognition, August 2006 2: 776-779.
Boulgouris NV, Plataniotis KN, Hatzinakos D: Gait recognition using linear time normalization. Pattern Recognition 2006,39(5):969-979. 10.1016/j.patcog.2005.10.013
Han J, Bhanu B: Individual recognition using gait energy image. IEEE Transactions on Pattern Analysis and Machine Intelligence 2006,28(2):316-322.
Cutler R, Benabdelkader C, Davis L: Motion-based recognition of people in eigengait space. Proceedings of the IEEE International Conference on Automatic Face and Gesture Recognition, May 2002 254-259.
Lu H, Plataniotis KN, Venetsanopoulos AN: Coarse-to-fine pedestrian localization and silhouette extraction for the gait challenge data sets. Proceedings of the IEEE International Conference on Multimedia and Expo (ICME '06), July 2006, Toronto, Canada 1009-1012.
Migdal J, Grimson WEL: Background subtraction using Markov thresholds. Proceedings of the IEEE Workshop on Motion and Video Computing (MOTION '05), January 2007 58-65.
Lee L, Dalley G, Tieu K: Learning pedestrian models for silhouette refinement. Proceedings of the IEEE International Conference on Computer Vision, October 2003 1: 663-670.
Lu H, Plataniotis KN, Venetsanopoulos AN: MPCA: multilinear principal component analysis of tensor objects. IEEE Transactions on Neural Networks 2008,19(1):18-39.
Freund Y, Schapire RE: Experiments with a new boosting algorithm. Proceedings of the 13th International Conference on Machine Learning, July 1996, Bari, Italy 148-156.
Schapire RE: The boosting approach to machine learning: an overview. In Proceedings of the MSRI Workshop on Nonlinear Estimation and Classification, March 2003, Berkeley, Calif, USA. Edited by: Denison DD, Hansen MH, Holmes C, Mallick B, Yu B. Springer;
Viola P, Jones MJ: Robust real-time face detection. International Journal of Computer Vision 2004,57(2):137-154.
Skurichina M, Duin RPW: Bagging, boosting and the random subspace method for linear classifiers. Pattern Analysis and Applications 2002,5(2):121-135. 10.1007/s100440200011
Lu J, Plataniotis KN, Venetsanopoulos AN, Li SZ: Ensemble-based discriminant learning with boosting for face recognition. IEEE Transactions on Neural Networks 2006,17(1):166-178.
Yang P, Shan S, Gao W, Li SZ, Zhang D: Face recognition using Ada-Boosted Gabor features. Proceedings of the 6th IEEE International Conference on Automatic Face and Gesture Recognition, May 2004 356-361.
Li SZ, Chu RF, Liao SC, Zhang L: Illumination invariant face recognition using near-infrared images. IEEE Transactions on Pattern Analysis and Machine Intelligence 2007,29(4):627-639.
Lathauwer LD, Moor BD, Vandewalle J: A multilinear singular value decomposition. SIAM Journal on Matrix Analysis and Applications 2000,21(4):1253-1278. 10.1137/S0895479896305696
Bader BW, Kolda TG: Algorithm 862: MATLAB tensor classes for fast algorithm prototyping. ACM Transactions on Mathematical Software 2006,32(4):635-653. 10.1145/1186785.1186794
Lathauwer LD, Moor BD, Vandewalle J:On the best rank-1 and rank-
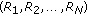 approximation of higher-order tensors. SIAM Journal on Matrix Analysis and Applications 2000,21(4):1324-1342. 10.1137/S0895479898346995
approximation of higher-order tensors. SIAM Journal on Matrix Analysis and Applications 2000,21(4):1324-1342. 10.1137/S0895479898346995Loog M, Duin RPW, Haeb-Umbach R: Multiclass linear dimension reduction by weighted pairwise Fisher criteria. IEEE Transactions on Pattern Analysis and Machine Intelligence 2001,23(7):762-766. 10.1109/34.935849
Phillips PJ, Sarkar S, Robledo I, Grother P, Bowyer KW: The gait identification challenge problem: data sets and baseline algorithm. Proceedings of the 16th International Conference on Pattern Recognition (ICPR '02), August 2002, Quebec, Canada 1: 385-388.
Acknowledgments
The authors would like to thank the anonymous reviewers for their insightful comments. The authors would also like to thank Professor Sudeep Sarkar from the University of South Florida for kindly providing us with the Gait Challenge datasets. This work is partially supported by the Ontario Centres of Excellence through the Communications and Information Technology Ontario Partnership Program and the Bell University Laboratories at the University of Toronto.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Lu, H., Plataniotis, K. & Venetsanopoulos, A. Boosting Discriminant Learners for Gait Recognition Using MPCA Features. J Image Video Proc 2009, 713183 (2009). https://doi.org/10.1155/2009/713183
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1155/2009/713183

 ,
, 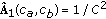 ,
, 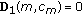 ,
,  ,
,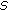 samples are selected to form the initial training set
samples are selected to form the initial training set 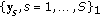 ,
,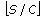 or
or 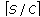 samples from each class, where
samples from each class, where  and
and  are
are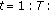
 ) Get
) Get 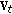 from
from 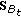 and
and  constructed from
constructed from 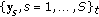 and project
and project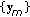 to
to  .
. ) Get hypothesis
) Get hypothesis 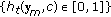 by applying the nearest neighbor classi-
by applying the nearest neighbor classi-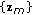 .
. ) Calculate
) Calculate 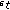 , the pseudo-loss of
, the pseudo-loss of 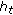 , from (12).
, from (12).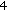 ) Set
) Set 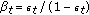 .
.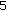 ) Update
) Update 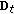 :
: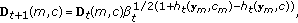
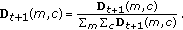
 ) Update
) Update 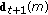 ,
, 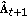 and
and 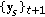 accordingly.
accordingly.
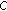 samples added to the pool of training sample for subsequent learning.
samples added to the pool of training sample for subsequent learning.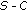 samples among all the rest samples, regardless of their class labels so that together with the
samples among all the rest samples, regardless of their class labels so that together with the  samples selected in the previous step,
samples selected in the previous step, 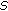 samples are chosen for subsequent boosting.
samples are chosen for subsequent boosting.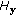 for input to LDA learners, the LDA feature vector dimension
for input to LDA learners, the LDA feature vector dimension 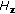 , the number of LDA training samples for LDA learner input
, the number of LDA training samples for LDA learner input  , and the regularization parameter
, and the regularization parameter  on boosting recognition performance,
on boosting recognition performance,
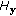 :
: 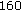 ,
,  ,
, 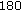 ,
,  ,
, 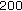 ,
, 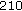 ,
, 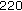 .
.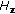 :
: 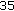 ,
, 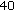 ,
, 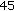 ,
,  ,
, 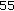 ,
, 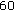 ,
,  ,
, 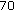 .
.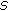 :
: 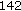 ,
, 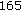 ,
,  ,
, 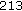 ,
, 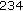 ,
,  ,
,  .
. :
: 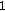 ,
, 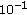 ,
,  ,
,  ,
,  .
.
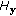 ,
,  ,
, 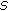 , and
, and  on Boosting
on Boosting




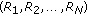 approximation of higher-order tensors. SIAM Journal on Matrix Analysis and Applications 2000,21(4):1324-1342. 10.1137/S0895479898346995
approximation of higher-order tensors. SIAM Journal on Matrix Analysis and Applications 2000,21(4):1324-1342. 10.1137/S0895479898346995