- Research Article
- Open access
- Published:
Iterative Multiview Side Information for Enhanced Reconstruction in Distributed Video Coding
EURASIP Journal on Image and Video Processing volume 2009, Article number: 591915 (2009)
Abstract
Distributed video coding (DVC) is a new paradigm for video compression based on the information theoretical results of Slepian and Wolf (SW) and Wyner and Ziv (WZ). DVC entails low-complexity encoders as well as separate encoding of correlated video sources. This is particularly attractive for multiview camera systems in video surveillance and camera sensor network applications, where low complexity is required at the encoder. In addition, the separate encoding of the sources implies no communication between the cameras in a practical scenario. This is an advantage since communication is time and power consuming and requires complex networking. In this work, different intercamera estimation techniques for side information (SI) generation are explored and compared in terms of estimating quality, complexity, and rate distortion (RD) performance. Further, a technique called iterative multiview side information (IMSI) is introduced, where the final SI is used in an iterative reconstruction process. The simulation results show that IMSI significantly improves the RD performance for video with significant motion and activity. Furthermore, DVC outperforms AVC/H.264 Intra for video with average and low motion but it is still inferior to the Inter No Motion and Inter Motion modes.
1. Introduction
Multiview video is attractive for a wide range of applications such as free viewpoint television (FTV) [1] and video surveillance camera networks. The increased use of multiview video systems is mainly due to the improvements in video technology. In addition, the reduced cost of cameras encourages the deployment of multiview video systems.
FTV is one of the promising applications of multiview. FTV is a 3D multiview system that allows viewing the scene from a view point chosen by the viewer. Video surveillance is another area where multiview can be beneficial for monitoring purposes. In addition, the multiple views can be used to improve the performance of event detection and recognition algorithms. However, the amount of data generated by multiview systems increases rapidly with the number of cameras. This makes data compression a key issue in such systems.
In DVC [2], the source statistics are exploited at the decoder by computing the SI of the WZ frame using different techniques. In this paper, a review of different SI techniques for multiview DVC is first provided, including a thorough evaluation of their estimation quality, complexity, and RD performance. Moreover, all the SI techniques are combined in the ground truth (GT) fusion, which combines the different SIs using the original WZ frame at the decoder. Even though this is not feasible in practice, it gives the maximum achievable DVC performance. Further, a new technique called iterative multiview side information (IMSI) is proposed to improve the DVC RD performance especially for video with significant motion. IMSI uses an initial SI to decode the WZ frame and then constructs a final SI which is used in a second reconstruction iteration. Finally, the performance of multiview DVC is compared with respect to AVC/H.264 [3] Intra, Inter No Motion (i.e., zero motion vectors), and Inter Motion.
The paper is structured as follows. First, the paradigm of distributed video coding is presented in Section 2. Multiview DVC is described in Section 3, whereas, Section 4 reviews the different intercamera estimation techniques. The IMSI technique is proposed in Section 5. Then, the test material and simulation results are presented and discussed in Section 6. Finally, some concluding remarks are drawn in Section 7.
2. Distributed Video Coding (DVC)
2.1. Theoretical DVC
DVC is the result of the information-theoretic bounds established for distributed source coding (DSC) by Slepian and Wolf [4] for lossless coding, and by Wyner and Ziv [5] for lossy coding with SI at the decoder. Lossless DSC refers to two correlated random sources separately encoded and jointly decoded by exploiting the statistical dependencies.
If we consider two statistically dependent random sequences X and Y, rates  and
and  can be achieved by entropy coding such that
can be achieved by entropy coding such that  and
and  where
where  and
and  are the entropies of X and Y, respectively. The Slepian-Wolf theorem proves that a better rate can be achieved with joint decoding and gives tighter bounds for the total rate
are the entropies of X and Y, respectively. The Slepian-Wolf theorem proves that a better rate can be achieved with joint decoding and gives tighter bounds for the total rate  The admissible rate region established by SW, which corresponds to the shaded area depicted in Figure 1, is defined by
The admissible rate region established by SW, which corresponds to the shaded area depicted in Figure 1, is defined by

Decoding with SI is considered as a special case of DSC. In this case, the source X depends on some SI Y, which corresponds to the black dot on the region border in Figure 1. Later on, Wyner and Ziv established bounds for lossy compression with SI at the decoder as an extension to the Slepian and Wolf theorem. In this case, the source X is encoded without having access to the SI Y. On the other hand, the decoder has access to the SI to produce X with a certain distortion D.
2.2. Practical DVC
Figure 2 shows the DVC architecture used in this work [6].
At the encoder, the frames are separated into two sets. The first one is the key frames which are fed to a conventional AVC/H.264 Intra encoder. The second set is the WZ frames. The latter are transformed and then quantized prior to WZ encoding. The same  separable integer transform as in AVC/H.264 is used with properties similar to the discrete cosine transform (DCT) [7]. Then, the same bands are grouped together and the different bit planes are extracted and then fed to a turbo encoder [8]. The latter offers near-channel capacity error correcting capability. Furthermore, a cyclic redundancy check (CRC) [9] is computed for each quantized bit plane and transmitted to the decoder. The frequency of the key frames is defined by the group of pictures (GOPs).
separable integer transform as in AVC/H.264 is used with properties similar to the discrete cosine transform (DCT) [7]. Then, the same bands are grouped together and the different bit planes are extracted and then fed to a turbo encoder [8]. The latter offers near-channel capacity error correcting capability. Furthermore, a cyclic redundancy check (CRC) [9] is computed for each quantized bit plane and transmitted to the decoder. The frequency of the key frames is defined by the group of pictures (GOPs).
At the decoder, the key frames are conventionally decoded and then used to generate the SI for the WZ decoder. In the monoview case, motion compensation temporal interpolation (MCTI) [10] is used to generate the SI. For this purpose, MCTI uses the key frames to perform motion estimation. The resulting motion vectors are interpolated at midpoint as illustrated in Figure 3.
A virtual channel is used to model the correlation between the DCT coefficients of the original and SI frames. It is shown that the residual of the DCT coefficients follows the Laplacian distribution [2]. The reconstruction process [11] uses the SI along with decoded bins to recover the original frame up to a certain quality. The decoder accepts the SI DCT value as a reconstructed one if it fits into the quantization interval corresponding to the decoded bin. Otherwise, it truncates the DCT value into the quantization interval. This DVC scheme is decoder driven as the request for parity bits from the encoder is performed via a feedback channel until successful decoding. The decoding is considered successful if the decoded bit plane error probability is lower than  and its CRC matches the one received from the encoder.
and its CRC matches the one received from the encoder.
The multiview DVC scheme used in this research is exactly the same as the monoview DVC described above except for the SI extraction module as it is explained further in Section 3.
3. Multiview DVC (MDVC)
MDVC is a solution that allows independent encoding of the cameras and joint decoding of the different video streams as shown in Figure 4.
It differs from monoview DVC in the decoder. More precisely, the SI is constructed not only using the frames within the same camera but using frames from the other cameras as well.
A fusion technique between temporal and homography-based side information is introduced in [12]. The fusion considers the previous and the forward frames as predictors of the WZ frame. The logical operation OR is used to combine the different predictors for each pixel. In other words, MCTI is chosen if it is a better predictor than homography for at least one of the two frames. Otherwise, homography is chosen as predictor as illustrated in Figure 5. The results in [12] report that the fusion outperforms monoview DVC by around  dB for video with significant motion for a spatial resolution of
dB for video with significant motion for a spatial resolution of  at 15 fps for a three cameras setup. In the latter, only the central camera contains WZ frames while the side ones are conventionally coded in Intra mode. This is called decoder-driven fusion.
at 15 fps for a three cameras setup. In the latter, only the central camera contains WZ frames while the side ones are conventionally coded in Intra mode. This is called decoder-driven fusion.
Decoder-driven fusion [ 12 ].
Artigas et al. [13] proposed two novel fusion techniques between temporal and intercamera side information. In the first technique, temporal motion interpolation is performed between the previous and the forward frames from the side cameras. The result is subtracted from the current frame and then thresholded to obtain a binary mask. The latter is projected to the central camera to perform the fusion as shown in Figure 6(a). The second algorithm uses the previous and the forward frames as predictors for the current frame on the side cameras to compute a reliability mask. The latter is projected to the central camera and used to perform the fusion as depicted in Figure 6(b). It is reported that the fusions improve the average PSNR of the SI using high resolution video ( at 15 fps). On the other hand, the RD performance of DVC is not investigated, and the simulations are run using the originals, which is in practice not feasible. Moreover, depth maps are required to perform the intercamera estimation which is a hard problem for complex real-world scenes.
at 15 fps). On the other hand, the RD performance of DVC is not investigated, and the simulations are run using the originals, which is in practice not feasible. Moreover, depth maps are required to perform the intercamera estimation which is a hard problem for complex real-world scenes.
Fusion techniques proposed by Artigas et al. [13].Motion estimation is performed on the side camera to compute a fusion mask for the central cameraFrame difference w.r.t the previous and forward frames on the side camera is used to compute the fusion mask
In [14], the wavelet transform is combined with turbo codes to encode a multiview camera array in a distributed way. At the decoder, a fusion technique is introduced to combine temporal and homography-based side information. It thresholds the motion vectors and the difference between the corresponding backward and forward estimations to obtain a fusion mask. The mask assigns the regions with significant motion vector and estimation error to homography SI, and the rest is assigned to temporal SI (i.e., regions with low motion and relatively small prediction error). It is reported that the hybrid SI outperforms the temporal one by around 1.5 dB in PSNR. In addition, it outperforms H.263+ Intra by around  dB. A video content with spatial resolution
dB. A video content with spatial resolution  is used in the evaluation.
is used in the evaluation.
Further, a flexible estimation technique that can jointly utilize temporal and view correlations to generate side information is proposed in [15]. More specifically, the current pixel in the WZ frame is mapped using homography to the left and right camera frames. Then, AVC/H.264 decision modes are applied to the pixel blocks in the left and right camera frames. If both resulting modes are intermodes, the SI value is taken from temporal SI. Otherwise, it is taken from homography SI. The simulation results show that this technique significantly outperforms conventional H.263+ Intra coding. Nevertheless, comparison with AVC/H.264 Intra would be beneficial as it represents state-of-the-art for conventional coding.
A fusion technique based on some prior knowledge of the original video is introduced in [16]. This is called encoder-driven fusion. Initially, a binary mask is calculated at the encoder as illustrated in Figure 7. It is compressed using a bilevel image compression [17] encoder and then transmitted to the decoder.
The encoder-driven fusion at the encoder side [ 16 ].
For each pixel, the mask informs the decoder whether the previous or the forward pixel is a better predictor of the same pixel in the original frame to perform fusion at the decoder (Figure 8). The results report a maximum gain up to 1.0 dB over monoview DVC in the same conditions as [12]. Furthermore, there is a slight increase in the encoder complexity as it has to perform the additional task of compressing the binary mask.
The encoder-driven fusion at the decoder side [ 16 ].
In [18], coding of multiview image sequences with video sensors connected to a central decoder is investigated. The N sensors are organized in an array to monitor the same scene from different views as shown in Figure 9. Only decoders 2 to N perform DVC using disparity compensated output of decoder 1. In addition, the video sensors are able to exploit temporal correlation using a motion compensated lifted wavelet transform [19] at the encoder. The proposed scheme reduces the bit rate by around 10% by performing joint decoding when compared to separate decoding for video content at 30 fps and  spatial resolution.
spatial resolution.
Distributed coding scheme with disparity compensation at the central decoder [ 18 ].
Finally, ways of improving the performance of multiview DVC are explored in [20]. Several modes to generate homography-based SI are introduced. The homography is estimated using a global motion estimation technique. The results show an improvement of SI quality by around 6.0 dB and a gain in RD performance by around  dB for video content with a spatiotemporal resolution of
dB for video content with a spatiotemporal resolution of  at 15 fps. However, the reported results assume an ideal fusion mask, which requires the knowledge of the original at the decoder. This is not feasible in a practical scenario.
at 15 fps. However, the reported results assume an ideal fusion mask, which requires the knowledge of the original at the decoder. This is not feasible in a practical scenario.
4. Intercamera Prediction
In this section, different SI techniques for multiview DVC are reviewed. The different techniques are described for 3 cameras setup, where the central camera is predicted from both neighboring cameras, as depicted in Figure 10.
4.1. Disparity Compensation View Prediction (DCVP)
DCVP [16] is based on the same idea as MCTI, but the motion compensation is performed between the frames from the side cameras. A slight modification is applied to DCVP to improve the SI quality. Instead of interpolating the motion vectors at midpoint, an optimal weight is computed in [16]. For this purpose, the first frame of each camera is conventionally decoded. Then, motion compensation is performed between the side camera frames. The motion vectors are weighted with the weights  Further, the SI PSNR is computed for each weight. The weight with maximum PSNR is maintained and used for the rest of the sequence. Nevertheless, the SI generated by DCVP has usually a poorer quality than the one generated by MCTI. This is due to the larger disparity between the side camera frames when compared to the one between the previous and forward frames.
Further, the SI PSNR is computed for each weight. The weight with maximum PSNR is maintained and used for the rest of the sequence. Nevertheless, the SI generated by DCVP has usually a poorer quality than the one generated by MCTI. This is due to the larger disparity between the side camera frames when compared to the one between the previous and forward frames.
4.2. Homography
The homography, H, is a  matrix transforming one view camera plane to another one as shown in Figure 11.
matrix transforming one view camera plane to another one as shown in Figure 11.
It uses eight parameters a, b, c, d, e, f, g, and h. The homography maps a point  from one plane to a point
from one plane to a point  in the second plane up to a scale
in the second plane up to a scale  such that
such that

This model is suitable when the scene can be approximated by a planar surface, or when the scene is static and the camera motion is a pure rotation around its optical center. The homography can be calculated using various techniques. In this work, we consider a global motion estimation technique introduced in [21] to compute the homography. The parameters are calculated such that the sum of squared differences  between the reference frame and the warped side frame is minimized:
between the reference frame and the warped side frame is minimized:

where  and
and  are the pixels from the warped and reference frames, respectively. The problem is solved using the Levenberg-Marquardt gradient descent algorithm to iteratively estimate the parameters. To remove the influence of such outliers, a truncated quadratic is used. In other words, only pixels for which the absolute value of the error term is below a certain threshold are taken into account in the estimation process, other pixels are ignored. Therefore, the algorithm will count mainly for global motion
are the pixels from the warped and reference frames, respectively. The problem is solved using the Levenberg-Marquardt gradient descent algorithm to iteratively estimate the parameters. To remove the influence of such outliers, a truncated quadratic is used. In other words, only pixels for which the absolute value of the error term is below a certain threshold are taken into account in the estimation process, other pixels are ignored. Therefore, the algorithm will count mainly for global motion

where T is a threshold.
In multiview DVC, the warped frame is computed from the left ( ) and right (
) and right ( ) camera frames as shown in Figure 12. Therefore, three side information are possible. The one entirely warped from each side camera and the average (
) camera frames as shown in Figure 12. Therefore, three side information are possible. The one entirely warped from each side camera and the average ( ) of both side cameras. The latter is the only one considered in this work.
) of both side cameras. The latter is the only one considered in this work.
The advantage of this technique is that once the homography relating the central camera with the side ones is estimated, computing the SI becomes very simple in terms of computational complexity when compared to techniques based on exhaustive block-based motion estimation. Moreover, this technique is suitable for scenarios, where the global motion is highly dominant with respect to local variations as it would generate a good estimation in this case. On the other hand, if the scene has multiple significant objects moving in different directions, the estimation would be of a poor quality as the technique would only account for global motion.
4.3. View Synthesis Prediction (VSP)
The previously mentioned techniques do not take advantage of some important features of multiview. That is, the speed at which an object is moving in a view depends on its depth information. In addition to this, rotations, zooms, and different intrinsic parameters are difficult to model using a motion vector, which is a simple translational model. Furthermore, the homography tries to estimate a global motion and ignores local motion using a truncated error function, which is not the case of VSP [22]. In the latter, the camera parameters, intrinsic and extrinsic, are used to predict one camera view from its neighbors.
For simplicity, the case of one neighboring camera is considered as shown in Figure 13. The view from camera  can be synthesized from camera
can be synthesized from camera  Each pixel
Each pixel  from camera
from camera  is projected into the 3D world reference using its depth information:
is projected into the 3D world reference using its depth information:

where A is the intrinsic parameters matrix, and R and T are the rotation and translation matrices with respect to the 3D world reference. Moreover, the depth information is equal to  which corresponds to the Z coordinate of the point in the 3D world coordinates. It is substituted in (5), and the resulting system is solved for
which corresponds to the Z coordinate of the point in the 3D world coordinates. It is substituted in (5), and the resulting system is solved for  and
and  Then, the 3D point is projected back to the 2D plane of camera
Then, the 3D point is projected back to the 2D plane of camera  This process is performed for each pixel of camera
This process is performed for each pixel of camera 
In the multiview camera setup used in this research, the pixel in the central camera is mapped to both side cameras. The pixel value is taken as average of both side camera pixels.
The drawback of this technique is the difficulty to estimate depth for real-world complex scenes. In addition, the quality of the SI depends on the precision of the camera calibration and depth estimation.
4.4. View Morphing (VM)
Image morphing can generate compelling 2D transitions between images. However, differences in object pose or viewpoint often cause unnatural distortions in image morphs. Using basic principles of projective geometry, one can perform a simple extension to image morphing that correctly handles 3D projective camera and scene transformations. The view morphing requires the computation of the fundamental matrix, which is the algebraic representation of epipolar geometry. Suppose that we have a point  in the 3D world coordinates. This point is visible in both cameras with optical centers
in the 3D world coordinates. This point is visible in both cameras with optical centers  and
and  as
as  and
and  respectively. The three points
respectively. The three points 
 and
and  define a plane called the epipolar plane
define a plane called the epipolar plane  The line intersection of the epipolar plane with each image plane is called an epipolar line as shown in Figure 14. The fundamental matrix is derived from the mapping between a point in one camera and its epipolar line in the other camera. Therefore, matching points should be calculated between the two images.
The line intersection of the epipolar plane with each image plane is called an epipolar line as shown in Figure 14. The fundamental matrix is derived from the mapping between a point in one camera and its epipolar line in the other camera. Therefore, matching points should be calculated between the two images.
VM [23] is used to get an image from a virtual camera that could be placed between two real cameras as shown in Figure 15. The input of the view morphing algorithm is two images from real cameras and information about the correspondences between regions in the two images or projection matrices of the side cameras from 3D world coordinates to 2D coordinates in each camera plane. The output of the algorithm is a synthesized image (i.e., a view from the virtual camera).
The VM of a virtual camera with optical  is illustrated in Figure 16. Initially, both images
is illustrated in Figure 16. Initially, both images  and
and  are warped across the scanlines to get
are warped across the scanlines to get  and
and  respectively, which are in the same plane. The latter are morphed across the position of the virtual camera
respectively, which are in the same plane. The latter are morphed across the position of the virtual camera  to get
to get  Finally,
Finally,  is unwarped to get
is unwarped to get  As in the case of DCVP, an optimal weight
As in the case of DCVP, an optimal weight  is computed for the virtual camera
is computed for the virtual camera  such that the PSNR is maximized for the warped frame with respect to the central view frame.
such that the PSNR is maximized for the warped frame with respect to the central view frame.
The problem with VM is that it works very well for simple scenes with a central object infront a uniform background. In this case, extracting matched feature points with a high degree of accuracy from the scene is simple as these points are used to compute the fundamental matrix. On the other hand, VM fails for real-world scenes as the matched feature points task becomes a more challenging task.
4.5. Multiview Motion Estimation (MVME)
MVME [24] finds the motion vectors in the side cameras and then applies them to the central camera to estimate the WZ frame as shown in Figure 17. The motion vectors computed in one view should be transformed before being used in another view. Nevertheless, they can be directly reused if all the cameras lie in the same plane and point in the same direction.
First, a disparity vector is obtained by block-based full search between the WZ and the intracameras for frame
is obtained by block-based full search between the WZ and the intracameras for frame  The vector
The vector  estimates the location of each block from the WZ camera in the intracamera. Then, the motion vector
estimates the location of each block from the WZ camera in the intracamera. Then, the motion vector is computed by searching in frame k in the intracamera for the best match for the block obtained in the previous step as illustrated in Figure 18(a). Finally, the motion vector
is computed by searching in frame k in the intracamera for the best match for the block obtained in the previous step as illustrated in Figure 18(a). Finally, the motion vector is applied to the aligned block in frame k in the WZ camera as depicted in Figure 18(b).
is applied to the aligned block in frame k in the WZ camera as depicted in Figure 18(b).
(a) Motion estimation scheme and (b) motion compensation scheme [ 24 ].
Figure 19 shows the possible motion paths to estimate the WZ frame, which are a total of 8 paths, 4 inner paths, and 4 outer paths, each generating one estimate. The inner paths are computed as described above by performing disparity estimation followed by motion estimation on the intracamera (Figure 19(a)). The outer paths are computed by doing the opposite of inner paths computation, starting with motion estimation on the intracamera followed by disparity estimation (Figure 19(b)). The simplest way to generate the final SI is by taking the average of these estimates. A better strategy is to compute a reliability measure for each path on a block or pixel basis and weight the estimates before taking the sum. For this purpose, mean square error (MSE) or mean absolute difference (MAD) computed between the original and the candidate blocks is used as a reliability measure.
The 8 possible paths when using two intracameras and two reference frames in each camera [24]. Inner pathsOuter paths
5. Iterative Multiview Side Information (IMSI)
We initially introduced iterative SI for the monoview scenario in [25], where the final SI depends not only on the key frames but also on the WZ bits as well. This final SI is used to refine the reconstruction of the decoded WZ frame. This is done by running the reconstruction process in a second iteration to enhance the quality of the decode frame. The process of IMSI is illustrated in Figure 20. IMSI differs from monoview iterative SI [25] in the fact that the initial SI depends on the input video in the multiview case. In the latter, the refinement process is applied to all the blocks, while a threshold is used to select the refined blocks based on the estimation error in [25].
Initially, the reconstruction process of DVC is described in this section. Then, IMSI is introduced.
5.1. DVC Reconstruction
This stage in the decoding process is opposite to the quantization step at the encoder. After turbo decoding, the decoder knows perfectly the quantization bin of each decoded band. Relying on the assumption that the WZ frame is correlated with the SI, the reconstruction block uses the SI along with decoded bins to improve the reconstruction quality as described in [11]. The principal consists in either accepting an SI value as a reconstructed value if it fits into the quantization interval corresponding to the decoded bin or truncating the SI value into this quantization interval. The reconstruction is performed independently for every transform coefficient of every band.
Let  be the SI value,
be the SI value,  the decoded quantized index,
the decoded quantized index,  the quantization step, and
the quantization step, and  the reconstructed value. In the case of the DC band, the reconstructed value
the reconstructed value. In the case of the DC band, the reconstructed value  is computed as
is computed as

For the AC bands, the reconstructed value  is computed in a similar way. The only difference is that a quantizer with a dead zone is used for the AC coefficients as they take positive and negative values. On the other hand, the DC coefficient takes only positive value.
is computed in a similar way. The only difference is that a quantizer with a dead zone is used for the AC coefficients as they take positive and negative values. On the other hand, the DC coefficient takes only positive value.
5.2. IMSI for Enhanced Reconstruction
Hereafter, the proposed IMSI is described.
-
(i)
First, the initial SI to use in the WZ frame decoding is chosen depending on the nature of the video. This is done by computing the average luma variation per pixel between the key frames at the decoder, which is compared to a threshold. If it is below the threshold, the motion is considered not significant and MCTI is used as the initial SI. Otherwise, MVME is taken as initial SI. This is motivated by the results presented further in Section 6.2. Namely, MCTI shows better estimation quality for low-motion video content. On the other hand, MVME is shown to have a better performance for video with significant motion.
-
(ii)
WZ decoding is performed using the initial SI, which implies turbo decoding followed by a first reconstruction stage.
-
(iii)
The decoded WZ frame from the first stage is then predicted by block-based motion search and compensation as in conventional video coding using four references: the previous, forward, left camera, and right camera frames. More specifically, for each block in the decoded frame, the best matching block with minimum distortion is selected using the square absolute difference (SAD) as the distortion metric as shown in Figure 21. This generates a final SI.
-
(iv)
Finally, the final SI is used in a second iteration in the reconstruction block.
It is important to stress the fact that this method does not use the original WZ but rather the decoded WZ frame using the initial SI. IMSI is expected to be efficient in situations where motion is significant as the difference in estimation quality between the initial and final SIs is more important. The reason is that the final SI is highly correlated with the WZ frame in the case of high activity video content. Therefore, most of the SI values map into the decoded bin in the reconstruction process (i.e., the SI value is taken as the reconstructed value). This produces a better reconstruction with lower distortion as less SI values are truncated into the quantization interval, when compared to the initial reconstruction phase, using the initial SI.
The improvement for low-motion video is negligible as both side information, initial and final, are close in terms of estimation quality.
IMSI generates a better estimation of the WZ frame than the initial SI, since it uses the decoded WZ frame from the first iteration to compute the estimation. On the other hand, the price to pay for this good estimation is the initial WZ rate spent to initially decode the WZ frame. In addition, there is an increase in the decoder complexity due to the additional motion search task.
6. Simulation Results
6.1. Test Material and Evaluation Methodology
The sequences Breakdancers, Ballet, and Uli shown in Figure 22 are used for evaluating the performance of the different SI techniques. Breakdancers and Ballet contain significant motion. This makes the motion estimation a difficult and challenging task. On the other hand, Uli is a conference-like video sequence, which contains more or less static video content. The spatial resolution is  for all the sequences. The temporal resolutions are 15 fps for Breakdancers and Ballet, and 25 fps for Uli.
for all the sequences. The temporal resolutions are 15 fps for Breakdancers and Ballet, and 25 fps for Uli.
In this paper, three camera views are used, and the performance is evaluated only for the central camera. For DVC simulations, the DISCOVER codec [6] is run with the following settings.
-
(i)
Only luminance data is coded.
-
(ii)
The central camera is the only one containing WZ frames. The side cameras (i.e., left and right) are conventionally encoded in the intramode, while the central one contains WZ frames, as depicted in Figure 10.
-
(iii)
Four RD points are computed per SI. They correspond to the following quantization matrices:
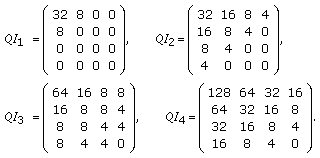 (7)
(7)Each element of the matrices corresponds to the number of quantization levels to the corresponding coefficient band. For example, the DC coefficient has 32, 32, 64, and 128 quantization levels, respectively, in the 1st, 2nd, 3rd, and 4th RD points, and so on.
-
(iv)
The same quantization parameter (QP) is used for the side cameras and the key frames of the central camera. A QP is defined per quantization matrix such that the decoded key and WZ frames have a similar quality.
-
(v)
The GOP size is equal to 2.
For AVC/H.264 coding, the publicly available reference software (JM 11.0) [26] is used with the following settings:
-
(a)
Intra, Inter No Motion, and Inter Motion modes. For the Inter No Motion mode, each motion vector is equal to zero, which means that each block in a P frame is predicted from the colocated block in the previous I frame. For the Inter Motion mode, the motion search range is set to 32. In both modes, the GOP size is equal to 12;
-
(b)
high profile with CABAC;
-
(c)
the
 transform enabled.
transform enabled.
6.2. Side Information Estimation Quality
In this section, the SI PSNR is evaluated for the SI techniques at the different RD points. Uli is not provided with depth maps. In addition, the feature point matching performs poorly due to highly textured scene background in the sequence. For this reason, the VSP and VM techniques are not evaluated for Uli.
For IMSI, Figure 23 shows the luma pixel variation between the key frames for the three video sequences at the highest RD point. By picking a threshold equal to 1.7, Breakdancers and Ballet are classified as sequences with significant motion (i.e., MVME is used as the initial SI) and Uli is classified as a low-motion video content (i.e., MCTI is used as the initial SI) at all RD points.
Figures 24, 25, and 26 show the SI PSNR for Breakdancers, Ballet, and Uli, respectively. Obviously, the GT fusion and IMSI produce the best estimation for all sequences at all RD points as they use, respectively, the original frame and the decoded WZ frame to construct the estimation. Thus, the comparison will mainly focus on the other SI techniques. For Breakdancers, MVME produces the best SI quality followed by MCTI. On the other hand, the worst performance is for VSP. However, VSP requires two input parameters, camera calibration, and depth estimation. The quality of the SI depends on the precision of these parameters. We can observe that most of the techniques perform quite well in terms of SI quality for this sequence as homography and DCVP are quite close to MCTI in estimation quality.
For Ballet, MVME produces the best SI quality followed by MCTI. Ballet contains motion but it is less significant than in the Breakdancers case. This explains the increase in PSNR gap between MCTI and the other SI techniques. As for Breakdancers, we have homography followed by DCVP, then VM, and finally VSP in a decreasing order in terms of SI quality.
Since Uli contains little motion, we expect MCTI and MVME to work very well, since MCTI performs a pure temporal interpolation and MVME performs an intercamera disparity estimation followed by a temporal motion estimation.
In summary, we can see clearly that MVME and MCTI produce by far better estimations than other SI generation techniques for Ballet and Uli. On the other hand, MVME, MCTI, homography, and DCVP are not very far from each other in terms of SI quality for Breakdancers.
Figure 27 illustrates the contribution of the different side information to the GT fusion for Breakdancers. It is obvious that MCTI has the largest contribution around  out of the total number of frame pixels. It is followed by homography-based SI. The homography is the one that brings most innovation to the GT fusion. MVME and DCVP are highly correlated with MCTI. This is explained by the fact that these methods are of the same block-based nature. Finally, VSP and VM have the worst contribution to the GT fusion.
out of the total number of frame pixels. It is followed by homography-based SI. The homography is the one that brings most innovation to the GT fusion. MVME and DCVP are highly correlated with MCTI. This is explained by the fact that these methods are of the same block-based nature. Finally, VSP and VM have the worst contribution to the GT fusion.
The contribution of the different side information to the GT fusion for Ballet is illustrated in Figure 28. As for Breakdancers, MCTI has the largest contribution, around  It is larger than in the Breakdancers case, since Ballet contains less motion than Breakdancers. It is followed by homography-based SI. Then, MVME comes in the third place followed by DCVP. Finally, VSP and VM are the worst in terms of contribution to the GT fusion.
It is larger than in the Breakdancers case, since Ballet contains less motion than Breakdancers. It is followed by homography-based SI. Then, MVME comes in the third place followed by DCVP. Finally, VSP and VM are the worst in terms of contribution to the GT fusion.
Since Uli contains low-motion content, MCTI has the largest contribution to the GT fusion, around  out of all pixels. It is followed by homography-based SI and then MVME. Furthermore, the rest of side information have a poor contribution to the GT fusion. This is illustrated in Figure 29.
out of all pixels. It is followed by homography-based SI and then MVME. Furthermore, the rest of side information have a poor contribution to the GT fusion. This is illustrated in Figure 29.
For the three sequences, homography-based SI is the one that brings most innovations to the GT fusion as it is the least correlated SI with MCTI. Therefore, we can conclude that possible fusion algorithms combining MCTI and homography-based SI represent a good tradeoff between performance improvement and complexity increase.
6.3. Side Information Complexity
The different techniques complexities are compared in terms of the total number of arithmetic operations (i.e., additions, subtractions, multiplications, and divisions) required to generate the side information. The image dimensions are the height, H, and the width, W. For the block-based methods, a search range  and block size
and block size  are considered.
are considered.
6.3.1. MCTI and DCVP
Both MCTI and DCVP have the same complexity. The only difference between both techniques is the input frames. For each block match,  subtractions are required. Then, the error is computed, which requires
subtractions are required. Then, the error is computed, which requires  additions. This is performed for each position within the search range. Thus,
additions. This is performed for each position within the search range. Thus,  operations are required to find a match for each block. Finally, all the blocks should be processed. Therefore,
operations are required to find a match for each block. Finally, all the blocks should be processed. Therefore,  is the number of operations required to estimate the motion between the two frames.
is the number of operations required to estimate the motion between the two frames.
6.3.2. MVME
There is a maximum of 8 paths. For each one, motion estimation is performed twice with the Intracamera and then across the side and the central cameras. Therefore,  operations are required for each path. Thus, a total of
operations are required for each path. Thus, a total of  operations is required for all the paths. In other words, MVME is approximately 16 times more complex than MCTI.
operations is required for all the paths. In other words, MVME is approximately 16 times more complex than MCTI.
6.3.3. Homography
Initially, the homography matrices are computed offline. A total of 15 operations is required to compute the mapping for each pixel using the  homography matrix. Therefore, the complexity of the homography-based side information generation from both view is
homography matrix. Therefore, the complexity of the homography-based side information generation from both view is 
6.3.4. VM
In VM, both side frames are warped, which requires  operations. Then, the resulting warped frames are morphed across the virtual camera position. The latter needs
operations. Then, the resulting warped frames are morphed across the virtual camera position. The latter needs  operations. Finally, the morphed frame is unwarped to obtain the side information. Therefore, the total complexity is
operations. Finally, the morphed frame is unwarped to obtain the side information. Therefore, the total complexity is  operations.
operations.
6.3.5. VSP
For each pixel, the projection from the image plane to the 3D world coordinates requires 38 operations. Moreover, the projection back to the central camera requires 23 operations. This is performed for each pixel, which results in a total complexity of  It important to mention that this estimation does not take into account the depth estimation. This complexity applies given that the depth map is already available.
It important to mention that this estimation does not take into account the depth estimation. This complexity applies given that the depth map is already available.
6.3.6. IMSI
The complexity of IMSI depends on the initial SI used, which is either MVME or MCTI. Then, the final SI generations requires  operations. This implies a maximum complexity of
operations. This implies a maximum complexity of  when MVME is used as the initial SI.
when MVME is used as the initial SI.
6.4. RD Performance
In this section, the RD plots for the different sequences are presented for the different side information. It is important to mention that only SI with a significant RD performance is presented. Therefore, the performance of VM and VSP is not plotted for Breakdancers and Ballet. For Uli, only IMSI, MCTI, and MVME are plotted as they significantly outperform the other side information. On the other hand, the GT fusion combines all the side information even the ones that are not plotted.
For Breakdancers, IMSI has the best RD performance out of all SI techniques as it is superior to MVME by around 0.4 dB and 0.7 dB at low and high bit rates, respectively. The SI quality is better for MVME than MCTI. This explains the performance gap between MVME and MCTI in Figure 30. This gap is more or less constant and around 0.2 dB. Further, homography and DCVP are inferior to MCTI by a maximum gap of around 1.0 dB and 2.0 dB, respectively, at high bit rates. At average bit rates, this gap is around 0.5 dB and 1.2 dB, respectively. The homography has a similar performance to MCTI at low bit rates and DCVP is inferior by 1.0 dB.
For IMSI, Figure 31 shows the quality of the reconstructed WZ frames for Breakdancers in the first and second reconstruction iterations for the highest RD point. In the initial one, around 13% of the SI values are truncated while this percentage is around 5% in the second reconstruction iteration resulting in a less-distorted reconstruction.
For Ballet, IMSI has the best RD performance slightly outperforming MVME by around 0.1 dB at high bit rates. Obviously, the performance improvement is less important than in the Breakdancers case as this sequence has less motion. Further, MVME and MCTI have a similar performance as shown in Figure 32. Even though MVME has a slightly better SI quality than MCTI for all RD points, it is not translated to a better RD performance. The reason is that the DVC scheme operates in the DCT domain not the pixel domain. Thus, a better SI PSNR, which is computed on the pixel values, does not automatically imply better performance for transform domain WZ decoding.
Finally, the reduction in the number of truncated SI values with IMSI is less significant (i.e., around 2%) for Ballet than in the case of Breakdancers. This leads to less improvement in the reconstruction as shown in Figure 33.
As mentioned previously, Uli contains very low-motion video content due to its nature. Therefore, both IMSI and MCTI have the best performance, but IMSI does not bring any improvement in this case. Both side information outperform MVME by around 0.5 dB as shown in Figure 34.
Next, the GT fusion, IMSI, and the fusion techniques introduced in [12, 16], combining MCTI and homography (i.e., the least correlated side information), are compared to AVC/H.264 Intra, Inter No Motion, and Inter Motion. The choice of the Intra and Inter No Motion modes is motivated by the fact they are very close to DVC in terms of encoding complexity. In addition, the DSC theorems state that the performance of a codec that performs joint encoding and decoding (i.e., Inter Motion Mode) should also be achievable (asymptotically) by a DVC codec.
For Breakdancers, even though the encoder driven fusion is slightly superior to IMSI at low bit rates but overall, IMSI produces the best performance out of the DVC techniques as it outperforms both fusion algorithms (Figure 35). The performance gap is more significant at high video quality. Nevertheless, IMSI is still inferior to AVC/H.264 in its different modes. This sequence is very challenging in terms of motion estimation, which generates a low-correlated SI with the WZ frame. This results in a poorer coding performance when compared to conventional codecs.
For Ballet, IMSI is superior to AVC/H.264 Intra by around 1.0 dB, and significantly outperformed by AVC/H.264 Inter No Motion and Inter Motion. Both fusions in this case improve the performance over IMSI. More specifically, the decoder-driven fusion improvement is around 0.25 dB. Moreover, the encoder-driven fusion improves the performance even further especially at low and average bit rates by a maximum gap of around 1.0 dB.
For Uli, IMSI, which is similar to MCTI in performance, improves the performance over AVC/H.264 Intra by around 3.0 dB. Moreover, it has a poorer performance than AVC/H.264 Inter No Motion and Inter Motion. The fusions do not result in any improvements as the decision is always made in favor of MCTI for the decoder-driven fusion. In other words, performing the fusion in this case is useless for Uli. For the encoder-driven fusion, the improvement in SI estimation quality is insignificant, and since additional rate is spent to send the binary mask, the overall performance drops below MCTI.
Overall, the performance of DVC is superior to AVC/H.264 Intra for two sequences out of three. On the other hand, it has a poorer performance than AVC/H.264 Inter Inter No Motion and Inter Motion for all the sequences, even with the GT fusion. Concerning DVC, IMSI is better for video content with very significant motion occupying a large part of the scene. MCTI is suitable for more or less static video content as it generates highly correlated SI with the WZ frame, resulting in superior compression efficiency than intraconventional coding, but inferior to conventional intercoding. For video with average motion, the encoder driven fusion produces the best performance for the DVC compression. Finally, the GT fusion shows that there still a large gap for improvement as it reduces the bit rate for DVC up to 50% for video with significant motion with respect to MCTI.
7. Conclusion
In this work, different SI generation techniques are studied for multiview DVC. For video with significant motion, the proposed IMSI significantly improves the performance over other SI techniques. It is followed by MVME and then MCTI. On the other hand, IMSI is more complex than MVME, which is much more complex than MCTI. For videos with average and low motion, MCTI and MVME improve the RD performance over AVC/H.264 Intra. Nevertheless, MCTI has the advantage of having a similar or better RD performance and being less complex than MVME in this case.
Further, we show that it is possible to reduce up to  the bit rate with respect to monoview DVC (i.e., MCTI) with the GT fusion. Nevertheless, the GT fusion requires the original video at the decoder, which is not feasible but it shows the maximum possible gain when the different SIs are ideally combined. It shows as well that MCTI, MVME, and DCVP generate highly correlated side information since they belong to the same block-based category techniques. On the other hand, MCTI and homography represent a good tradeoff between performance improvement and complexity increase. Moreover, fusion techniques combining these two side information show significant improvement for video with high motion.
the bit rate with respect to monoview DVC (i.e., MCTI) with the GT fusion. Nevertheless, the GT fusion requires the original video at the decoder, which is not feasible but it shows the maximum possible gain when the different SIs are ideally combined. It shows as well that MCTI, MVME, and DCVP generate highly correlated side information since they belong to the same block-based category techniques. On the other hand, MCTI and homography represent a good tradeoff between performance improvement and complexity increase. Moreover, fusion techniques combining these two side information show significant improvement for video with high motion.
Many improvements are possible over this work. Initially, a better fusion algorithm should be found to exploit the combination of the different side information without needing the original frame and close the gap on the GT fusion. Moreover, fusion between MCTI and homography should be considered as they produce the least-correlated side information, and represent a good tradeoff between performance improvement and complexity increase.
Further, the MVME technique is very complex. Therefore, the complexity of this technique can be reduced by using fast motion search techniques such as a multigrid [27] approach instead of a fixed block size in addition to an N-step [28] search instead of a full search.
Finally, the additional complexity in the IMSI technique can be significantly reduced by selecting the blocks for which the reestimation is performed as defined in [25]. More specifically, a block is reestimated in the final SI if the residual error between the initially decoded WZ frame and the initial SI is greater than a certain threshold for this block. Otherwise, the block from the initial SI is just copied into the final SI.
References
Free Viewpoint Television (FTV) http://www.tanimoto.nuee.nagoya-u.ac.jp/study/FTV
Girod B, Aaron AM, Rane S, Rebollo-Monedero D: Distributed video coding. Proceedings of the IEEE 2005,93(1):71-83.
Wiegand T, Sullivan GJ, Bjøntegaard G, Luthra A: Overview of the H.264/AVC video coding standard. IEEE Transactions on Circuits and Systems for Video Technology 2003,13(7):560-576.
Slepian D, Wolf J: Noiseless coding of correlated information sources. IEEE Transactions on Information Theory 1973,19(4):471-480. 10.1109/TIT.1973.1055037
Wyner A, Ziv J: The rate-distortion function for source coding with side information at the decoder. IEEE Transactions on Information Theory 1976,22(1):1-10. 10.1109/TIT.1976.1055508
Artigas X, Ascenso J, Dalai M, Klomp S, Kubasov D, Ouaret M: The DISCOVER codec: architecture, techniques and evaluation. Proceedings of the Picture Coding Symposium (PCS '07), November 2007, Lisbon, Portugal
Malvar HS, Hallapuro A, Karczewicz M, Kerofsky L: Low-complexity transform and quantization in H.264/AVC. IEEE Transactions on Circuits and Systems for Video Technology 2003,13(7):598-603. 10.1109/TCSVT.2003.814964
Berrou C, Glavieux A, Thitimajshima P: Near Shannon limit error-correcting coding and decoding: turbo-codes.1. Proceedings of the IEEE International Conference on Communications (ICC '93), May 1993, Geneva, Switzerland 2: 1064-1070.
Peterson WW, Brown DT: Cyclic codes for error detection. Proceedings of the IRE 1961,49(1):228-235.
Ascenso J, Brites C, Pereira F: Improving frame interpolation with spatial motion smoothing for pixel domain distributed video coding. Proceedings of the 5th EURASIP Conference on Speech and Image Processing, Multimedia Communications and Services, July 2005, Smolenice, Slovak
Aaron A, Zhang R, Girod B: Wyner-ziv coding for motion video. Proceedings of the 36th Asilomar Conference on Signals, Systems and Computers, November 2002, Pacific Grove, Calif, USA
Ouaret M, Dufaux F, Ebrahimi T: Fusion-based multiview distributed video coding. Proceedings of the 4th ACM International Workshop on Video Surveillance and Sensor Networks (VSSN '06), October 2006, Santa Barbara, Calif, USA 139-144.
Artigas X, Angeli E, Torres L: Side information generation for multiview distributed video coding using a fusion approach. Proceedings of the 7th Nordic Signal Processing Symposium (NORSIG '06), June 2007, Reykjavik, Iceland 250-253.
Guo X, Lu Y, Wu F, Gao W, Li S: Distributed multi-view video coding. Visual Communications and Image Processing (VCIP), January 2006, San Jose, Calif, USA, Proceedings of SPIE 6077:
Guo X, Lu Y, Wu F, Zhao D, Gao W: Wyner-ziv-based multiview video coding. IEEE Transactions on Circuits and Systems for Video Technology 2008,18(6):713-724.
Ouaret M, Dufaux F, Ebrahimi T: Multiview distributed video coding with encoder driven fusion. Proceedings of the European Conference on Signal Processing (EUSIPCO '07), September 2007, Poznan, Poland
Joint Bi-Level Image Experts Group http://www.jpeg.org/jbig
Flierl M, Girod B: Coding of multi-view image sequences with video sensors. Proceedings of the International Conference on Image Processing (ICIP '06), October 2006, Atlanta, Ga, USA 609-612.
Flierl M, Girod B: Video coding with motion-compensated lifted wavelet transforms. Signal Processing: Image Communication 2004,19(7):561-575. 10.1016/j.image.2004.05.002
Dufaux F, Ouaret M, Ebrahimi T: Recent advances in multiview distributed video coding. Mobile Multimedia/Image Processing for Military and Security Applications, April 2007, Orlando, Fla, USA, Proceedings of SPIE 6579: 1-11.
Dufaux F, Konrad J: Efficient, robust, and fast global motion estimation for video coding. IEEE Transactions on Image Processing 2000,9(3):497-501. 10.1109/83.826785
Martinian E, Behrens A, Xin J, Vetro A: View synthesis for multiview video compression. Proceedings of the 25th Picture Coding Symposium (PCS '06), April 2006, Beijing, China
Seitz SM, Dyer CR: View morphing. Proceedings of the 23rd Annual Conference on Computer Graphics and Interactive Techniques (SIGGRAPH '96), August 1996, New Orleans, La, USA 21-30.
Artigas X, Tarres F, Torres L: Comparison of different side information generation methods for multiview distributed video coding. Proceedings of the International Conference on Signal Processing and Multimedia Applications (SIGMAP '07), July 2007, Barcelona, Spain
Ye S, Ouaret M, Dufaux F, Ebrahimi T: Improved side information generation with iterative decoding and frame interpolation for distributed video coding. Proceedings of the 15th International Conference on Image Processing (ICIP '08), October 2008, San Deigo, Calif, USA 2228-2231.
AVC/H.264 software http://iphome.hhi.de/suehring/tml
Dufaux F: Multigrid Block Matching Motion Estimation for Generic Video Coding, Ph.D. thesis. Ecole Polytechnique Federale de Lausanne, Lausanne, Switzerland; 1994.
Coban MZ, Mersereau RM: Fast rate-constrained N-step search algorithm for motion estimation. Proceedings of the IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP '98), May 1998, Seattle, Wash, USA 5: 2613-2616.
Acknowledgments
This work was partially supported by the European project Discover (http://www.discoverdvc.org) (IST Contract 015314) and the European Network of Excellence VISNET II (http://www.visnet-noe.org) (IST Contract 1-038398), both funded under the European Commission IST 6th Framework Program. The authors also would like to acknowledge the use of the DISCOVER codec, a software which started from the IST WZ software developed at the Image Group from Instituto Superior Técnico (IST) of Lisbon by Catarina Brites, João Ascenso, and Fernando Pereira.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Ouaret, M., Dufaux, F. & Ebrahimi, T. Iterative Multiview Side Information for Enhanced Reconstruction in Distributed Video Coding. J Image Video Proc 2009, 591915 (2009). https://doi.org/10.1155/2009/591915
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1155/2009/591915























 transform enabled.
transform enabled.













