- Research Article
- Open access
- Published:
Smooth Adaptation by Sigmoid Shrinkage
EURASIP Journal on Image and Video Processing volume 2009, Article number: 532312 (2009)
Abstract
This paper addresses the properties of a subclass of sigmoid-based shrinkage functions: the non zeroforcing smooth sigmoid-based shrinkage functions or SigShrink functions. It provides a SURE optimization for the parameters of the SigShrink functions. The optimization is performed on an unbiased estimation risk obtained by using the functions of this subclass. The SURE SigShrink performance measurements are compared to those of the SURELET (SURE linear expansion of thresholds) parameterization. It is shown that the SURE SigShrink performs well in comparison to the SURELET parameterization. The relevance of SigShrink is the physical meaning and the flexibility of its parameters. The SigShrink functions performweak attenuation of data with large amplitudes and stronger attenuation of data with small amplitudes, the shrinkage process introducing little variability among data with close amplitudes. In the wavelet domain, SigShrink is particularly suitable for reducing noise without impacting significantly the signal to recover. A remarkable property for this class of sigmoid-based functions is the invertibility of its elements. This propertymakes it possible to smoothly tune contrast (enhancement, reduction).
1. Introduction
The Smooth Sigmoid-Based Shrinkage (SSBS) functions introduced in [1] constitute a wide class of WaveShrink functions. The WaveShrink (Wavelet Shrinkage) estimation of a signal involves projecting the observed noisy signal on a wavelet basis, estimating the signal coefficients with a thresholding or shrinkage function and reconstructing an estimate of the signal by means of the inverse wavelet transform of the shrunken wavelet coefficients. The SSBS functions derive from the sigmoid function and perform an adjustable wavelet shrinkage thanks to parameters that control the attenuation degree imposed to the wavelet coefficients. As a consequence, these functions allow for a very flexible shrinkage.
The present work addresses the properties of a subclass of the SSBS functions, the non-zero-forcing SSBS functions, hereafter called the SigShrink (Sigmoid Shrinkage) functions. First, we provide a discussion on the optimization of the SigShrink parameters in the context of WaveShrink estimation. The optimization exploits the new Stein Unbiased Risk of Estimation ((SURE), [2]) proposed in [3]. SigShrink performance measurements are compared to those obtained when using the parameterization of [3], which consists of a sum of Derivatives of Gaussian (DOG). We then address the main features of the SigShrink functions; artifact-free denoising and smooth contrast functions make SigShrink a worthy tool for various signal and image processing applications.
The presentation of this paper is as follows. Section 2 presents the SigShrink functions. Section 3 briefly describes the nonparametric estimation by wavelet shrinkage and addresses the optimization of the SigShrink parameters with respect to the new SURE approach described in [3]. Section 4 discusses the main properties of the SigShrink functions by providing experimental tests. These tests assess the quality of the SigShrink functions for image processing: adjustable and artifact-free denoising as well as contrast functions. Finally, Section 5 concludes this paper.
2. Smooth Sigmoid-Based Shrinkage
The family of real-valued functions defined by [1]

for  , are shrinkage functions satisfying the following properties.
, are shrinkage functions satisfying the following properties.
(P1) Smoothness. There is smoothness of the shrinkage function so as to induce small variability among data with close values;
(P2) Penalized Shrinkage. A strong (resp., a weak) attenuation is imposed for small (resp., large) data.
(P3) Vanishing Attenuation at Infinity. The attenuation decreases to zero when the amplitude of the coefficient tends to infinity.
Each  is the product of the identity function with a sigmoid-like function. A function
is the product of the identity function with a sigmoid-like function. A function  will hereafter be called a SigShrink (Sigmoid Shrinkage) function.
will hereafter be called a SigShrink (Sigmoid Shrinkage) function.
Note that  tends to
tends to  , which is a hard-thresholding function defined by
, which is a hard-thresholding function defined by

where  is the indicator function of a given set
is the indicator function of a given set  :
:  if
if  if
if  . It follows that
. It follows that  acts as a threshold. Note that
acts as a threshold. Note that  sets a coefficient with amplitude
sets a coefficient with amplitude  to half of its value and so minimizes the local variation (second derivative) around
to half of its value and so minimizes the local variation (second derivative) around  , since
, since  .
.
In addition, it is easy to check that, in Cartesian-coordinates, the points  , and
, and  belong to the curve of the function
belong to the curve of the function  for every
for every  . Indeed, according to (1), we have
. Indeed, according to (1), we have  and
and  for any
for any  . It follows that
. It follows that  parameterizes the curvature of the arc
parameterizes the curvature of the arc  , that is, the arc of the SigShrink function in the interval ]−
, that is, the arc of the SigShrink function in the interval ]− [. This curvature directly relates to the attenuation degree we want to apply to the wavelet coefficients. Consider the graph of Figure 1, where a SigShrink function is plotted in the positive half plan. Due to the antisymmetry of the SigShrink function, we only focus on the curvature of arc
[. This curvature directly relates to the attenuation degree we want to apply to the wavelet coefficients. Consider the graph of Figure 1, where a SigShrink function is plotted in the positive half plan. Due to the antisymmetry of the SigShrink function, we only focus on the curvature of arc  . Let
. Let  be the intersection between the abscissa axis and the tangent at point
be the intersection between the abscissa axis and the tangent at point  to the curve of the SigShrink function. The equation of this tangent is
to the curve of the SigShrink function. The equation of this tangent is  . The coordinates of point
. The coordinates of point  are
are  . We can easily control the arc
. We can easily control the arc  curvature via the angle, denoted by
curvature via the angle, denoted by  , between vector
, between vector  , which is fixed, and vector
, which is fixed, and vector  , which is carried by the tangent to the curve of
, which is carried by the tangent to the curve of  at point
at point  . The larger
. The larger  , the stronger the attenuation of the coefficients with amplitudes less than or equal to
, the stronger the attenuation of the coefficients with amplitudes less than or equal to  . For a fixed
. For a fixed  , the relation between angle
, the relation between angle  and parameter
and parameter  is
is

It easily follows from (3) that  ; when
; when  , then
, then  and
and  is the hard-thresholding function of (2). From (3), we derive that
is the hard-thresholding function of (2). From (3), we derive that  can be written as a function of
can be written as a function of  and
and  as follows:
as follows:

In practice, when  is fixed, the foregoing makes it possible to control the attenuation degree we want to impose to the data in
is fixed, the foregoing makes it possible to control the attenuation degree we want to impose to the data in  by choosing
by choosing  , which is rather natural, and calculating
, which is rather natural, and calculating  according to (4). Since we can control the shrinkage by choosing
according to (4). Since we can control the shrinkage by choosing  henceforth denotes the SigShrink function where
henceforth denotes the SigShrink function where  is given by (4). This interpretation of the SigShrink parameters makes it easier to find "nice" parameters for practical applications. Summarizing, the SigShrink computation is performed in three steps:
is given by (4). This interpretation of the SigShrink parameters makes it easier to find "nice" parameters for practical applications. Summarizing, the SigShrink computation is performed in three steps:
-
(1)
fix threshold
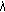 and angle
and angle 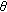 of the SigShrink function, with
of the SigShrink function, with  and
and  . Keep in mind that the larger
. Keep in mind that the larger  , the stronger the attenuation,
, the stronger the attenuation, -
(2)
compute the corresponding value of
 from (4),
from (4), -
(3)
shrink the data according to the SigShrink function
 defined by (1).
defined by (1).
Hereafter, the terms "attenuation degree" and "threshold" designate  and
and  , respectively. In addition, the notation
, respectively. In addition, the notation  will be preferred for calculations and statements. The notation
will be preferred for calculations and statements. The notation  , introduced just above, will be used for practical and experimental purposes since the attenuation degree
, introduced just above, will be used for practical and experimental purposes since the attenuation degree  is far more natural in practice than parameter
is far more natural in practice than parameter  . Some SigShrink graphs are plotted in Figure 2 for different values of the attenuation degree
. Some SigShrink graphs are plotted in Figure 2 for different values of the attenuation degree  (fixed threshold
(fixed threshold  ).
).
3. Sigmoid Shrinkage in the Wavelet Domain
3.1. Estimation via Shrinkage in the Wavelet Domain
Let us recall the main principles of the nonparametric estimation by wavelet shrinkage (the so-called WaveShrink estimation) in the sense of [4]. Let  stand for the sequence of noisy data
stand for the sequence of noisy data  where
where  is an unknown deterministic function, the random variables
is an unknown deterministic function, the random variables  are independent and identically distributed (iid), Gaussian with null mean and variance
are independent and identically distributed (iid), Gaussian with null mean and variance  , in short,
, in short,  for every
for every  .
.
In order to estimate  , we assume that an orthonormal transform, represented by an orthonormal matrix
, we assume that an orthonormal transform, represented by an orthonormal matrix  , is applied to
, is applied to  . The outcome of this transform is the sequence of coefficients
. The outcome of this transform is the sequence of coefficients

where  and
and  . The random variables
. The random variables  are iid and
are iid and  . The transform
. The transform  is assumed to achieve a sparse representation of the signal in the sense that, among the coefficients
is assumed to achieve a sparse representation of the signal in the sense that, among the coefficients  , only a few of them have large amplitudes and, as such, characterize the signal. In this respect, simple estimators such as "keep or kill" and "shrink or kill" rules are proved to be nearly optimal, in the Mean Square Error (MSE) sense, in comparison with oracles (see [4] for further details). The wavelet transform is sparse in the sense given above for smooth and piecewise regular signals [4]. Hereafter, the matrix
, only a few of them have large amplitudes and, as such, characterize the signal. In this respect, simple estimators such as "keep or kill" and "shrink or kill" rules are proved to be nearly optimal, in the Mean Square Error (MSE) sense, in comparison with oracles (see [4] for further details). The wavelet transform is sparse in the sense given above for smooth and piecewise regular signals [4]. Hereafter, the matrix  represents an orthonormal wavelet transform. Let
represents an orthonormal wavelet transform. Let  be the sequence resulting from the shrinkage of
be the sequence resulting from the shrinkage of  by using a function
by using a function  . We obtain an estimate of
. We obtain an estimate of  by setting
by setting  where
where  is the transpose, and thus, the inverse orthonormal wavelet transform.
is the transpose, and thus, the inverse orthonormal wavelet transform.
In [4], the hard and soft-thresholding functions are proposed for wavelet coefficient estimation of a signal corrupted by Additive, White and Gaussian Noise (AWGN). Using these thresholding functions adjusted with suitable thresholds, [4] shows that, in AWGN, the wavelet-based estimators thus obtained achieve within a factor of  of the performance achieved with the aid of an oracle. Despite the asymptotic near-optimality of these standard thresholding functions, we have the following limitations. The hard-thresholding function is not everywhere continuous and its discontinuities generate a high variance of the estimate; on the other hand, the soft-thresholding function is continuous but creates an attenuation on large coefficients, which results in an over smoothing and an important bias for the estimate [5]. In practice, these thresholding functions (and their alternatives "nonnegative garrote" function [6], "smoothly clipped absolute deviation" function [7]) yield musical noise in speech denoising and visual artifacts or over smoothing of the estimate in image processing (see, e.g., the experimental results given in Section 4.1). Moreover, although thresholding rules are proved to be relevant strategies for estimating sparse signals [4], wavelet representations of many signals encountered in practical applications such as speech and image processing fail to be sparse enough (see illustrations given in [8, Figure 3]). For a signal whose wavelet representation fails to be sparse enough, it is more convenient to impose the penalized shrinkage condition (P2) instead of zero forcing since small coefficients may contain significant information about the signal. Condition (P1) guarantees the regularity of the shrinkage process, and the role of condition (P3) is to avoid over smoothing of the estimate (noise mainly affects small wavelet coefficients). SigShrink functions are thus suitable functions for such an estimation since they satisfy (P1), (P2), and (P3) conditions. The following addresses the optimization of the SigShrink parameters.
of the performance achieved with the aid of an oracle. Despite the asymptotic near-optimality of these standard thresholding functions, we have the following limitations. The hard-thresholding function is not everywhere continuous and its discontinuities generate a high variance of the estimate; on the other hand, the soft-thresholding function is continuous but creates an attenuation on large coefficients, which results in an over smoothing and an important bias for the estimate [5]. In practice, these thresholding functions (and their alternatives "nonnegative garrote" function [6], "smoothly clipped absolute deviation" function [7]) yield musical noise in speech denoising and visual artifacts or over smoothing of the estimate in image processing (see, e.g., the experimental results given in Section 4.1). Moreover, although thresholding rules are proved to be relevant strategies for estimating sparse signals [4], wavelet representations of many signals encountered in practical applications such as speech and image processing fail to be sparse enough (see illustrations given in [8, Figure 3]). For a signal whose wavelet representation fails to be sparse enough, it is more convenient to impose the penalized shrinkage condition (P2) instead of zero forcing since small coefficients may contain significant information about the signal. Condition (P1) guarantees the regularity of the shrinkage process, and the role of condition (P3) is to avoid over smoothing of the estimate (noise mainly affects small wavelet coefficients). SigShrink functions are thus suitable functions for such an estimation since they satisfy (P1), (P2), and (P3) conditions. The following addresses the optimization of the SigShrink parameters.
3.2. SURE-Based Optimization of SigShrink Parameters
Consider the WaveShrink estimation described in Section 3.1. The risk function or cost used to measure the accuracy of a WaveShrink estimator  of
of  is the standard MSE. Since the transform
is the standard MSE. Since the transform  is orthonormal, this cost is
is orthonormal, this cost is

for a shrinkage function  . The SURE approach [2] involves estimating unbiasedly the risk
. The SURE approach [2] involves estimating unbiasedly the risk  . The SURE optimization then consists in finding the set of parameters that minimizes this unbiased estimate. The following result is a consequence of [3, Theorem 1].
. The SURE optimization then consists in finding the set of parameters that minimizes this unbiased estimate. The following result is a consequence of [3, Theorem 1].
Proposition 3.1.
The quantity  , where
, where  denotes
denotes  -norm and
-norm and

is an unbiased estimator of the risk  , where
, where  is a SigShrink function.
is a SigShrink function.
Proof.
From [3, Theorem 1], we have that

where  can be any differentiable shrinkage function that does not explode at infinity (see [3] for details). A SigShrink function is such a shrinkage function. Taking into account that the derivate of the SigShrink function
can be any differentiable shrinkage function that does not explode at infinity (see [3] for details). A SigShrink function is such a shrinkage function. Taking into account that the derivate of the SigShrink function  is
is

the result derives from (1), (8), and (9).
As a consequence of Proposition 3.1, we get that minimizing  of (6) amounts to minimizing the unbiased (SURE) estimator
of (6) amounts to minimizing the unbiased (SURE) estimator  given by (7). The next section presents experimental tests for illustrating the SURE SigShrink denoising of some natural images corrupted by AWGN. For every tested image and every noise standard deviation considered, the optimal SURE SigShrink parameters are those minimizing
given by (7). The next section presents experimental tests for illustrating the SURE SigShrink denoising of some natural images corrupted by AWGN. For every tested image and every noise standard deviation considered, the optimal SURE SigShrink parameters are those minimizing  , the vector
, the vector  representing the wavelet coefficients of the noisy image.
representing the wavelet coefficients of the noisy image.
3.3. Experimental Results
The SURE optimization approach for SigShrink is now given for some standard test images corrupted by AWGN. We consider the standard  -dimensional Discrete Wavelet Transform (DWT) by using the Symlet wavelet of order
-dimensional Discrete Wavelet Transform (DWT) by using the Symlet wavelet of order  ("sym8" in the Matlab Wavelet toolbox).
("sym8" in the Matlab Wavelet toolbox).
The SigShrink estimation is compared with that of the SURELET "sum of DOGs" (Derivatives Of Gaussian). SURELET (free MatLab software is avalaible at http://bigwww.epfl.ch/demo/suredenoising/) is a SURE-based method that moreover includes an interscale predictor with a priori information about the position of significant wavelet coefficients. For the comparison with SigShrink, we only use the "sum of DOGs" parameterization, that is, the SURELET method without inter-scale predictor and Gaussian smoothing. By so proceeding, we thus compare two shrinkage functions: SigShrink and "sum of DOGs."
In the sequel, the SURE SigShrink parameters (attenuation degree and threshold) are those obtained by performing the SURE optimization on the whole set of the detail DWT coefficients. The attenuation degree and threshold thus computed are then applied at every decomposition level to the detail DWT coefficients. We also introduce the SURE Level-Dependent SigShrink (SURE LD-SigShrink) parameters. These parameters are obtained by applying an SURE optimization at every detail (horizontal, vertical, diagonal) subimage located at the different resolution levels concerned (4 resolution levels in our experiments).
The tests are carried out with the following values for the noise standard deviation:  . For every value
. For every value  , 25 tests have been performed based on different noise realizations. Every test involves performing a DWT for the tested image corrupted by AWGN, computing the optimal SURE parameters (SigShrink and LD-SigShrink), applying the SigShrink function with these parameters to denoise the wavelet coefficients, and building an estimate of the corresponding image by applying the inverse DWT to the shrunken coefficients. For every test, the PSNR is calculated for the original image and the denoised image. The PSNR (in deciBel unit, dB), often used to assess the quality of a compressed image, is given by
, 25 tests have been performed based on different noise realizations. Every test involves performing a DWT for the tested image corrupted by AWGN, computing the optimal SURE parameters (SigShrink and LD-SigShrink), applying the SigShrink function with these parameters to denoise the wavelet coefficients, and building an estimate of the corresponding image by applying the inverse DWT to the shrunken coefficients. For every test, the PSNR is calculated for the original image and the denoised image. The PSNR (in deciBel unit, dB), often used to assess the quality of a compressed image, is given by

where  stands for the dynamics of the signal,
stands for the dynamics of the signal,  in the case of 8 bit-coded images.
in the case of 8 bit-coded images.
Table 1 gives the following statistics for the 25 PSNRs obtained by the SURE SigShrink, SURE LD-SigShrink, and "sum of DOGs" method: average value, variance, minimum, and maximum. Average values and variances for the SURE SigShrink and SURE LD-SigShrink parameters are given in Tables 2, 3, 4, and 5.
 . The DWT is computed by using the "sym8" wavelet. Some statistics are given in Tables 2, 3, 4, and 5 for the SigShrink and LD-SigShrink optimal SURE parameters.
. The DWT is computed by using the "sym8" wavelet. Some statistics are given in Tables 2, 3, 4, and 5 for the SigShrink and LD-SigShrink optimal SURE parameters. and
and  obtained by performing the SURE optimization on the whole set of the detail DWT coefficients. It follows from these results that the threshold height as well as the attenuation degree tends to be increasing functions of the noise standard deviation
obtained by performing the SURE optimization on the whole set of the detail DWT coefficients. It follows from these results that the threshold height as well as the attenuation degree tends to be increasing functions of the noise standard deviation  .
. . In addition, for every
. In addition, for every  considered, the attenuation degree as well as the threshold tends to decrease when the resolution level increases.
considered, the attenuation degree as well as the threshold tends to decrease when the resolution level increases.We use the Matlab routine fmincon to compute the optimal SURE SigShrink parameters. This function computes the minimum of a constrained multivariable function by using nonlinear programming methods (see Matlab help for the details). Note the following. First, one can use a test set and average the optimal parameter values on this set for application to images other than those used in the test set. By so proceeding, we avoid the systematic use of optimization algorithms such as fmincon on images that do not pertain to the test class. The low variability that holds among the optimal parameters given in Tables 2, 3, 4, and 5 ensures the robustness of the average values. Second, instead of using optimal parameters, one can use heuristic ones (calculated by taking into account the physical meaning of these parameters and the noise statistical properties) such as the standard minimax or universal thresholds, which are shown to perform well with SigShrink (see Section 4).
From Table 1, it follows that the 3 methods yield PSNRs of the same order. The level dependent strategy for SigShrink (LD-SigShrink) tends to achieve better results than the SigShrink and the "sum of DOGs." For every method, the difference (over the 25 noise realizations) between the minimum and maximum PSNR is less than 0.2 dB.
From Tables 2, 3, 4, and 5, we observe (concerning the optimal SURE SigShrink parameters) that
-
(i)
the threshold height as well as the attenuation degree tends to be increasing functions of the noise standard deviation
 ,
, -
(ii)
for every tested
 , the SURE level-dependent attenuation degree and threshold tend to decrease when the resolution level increase (see Table 4),
, the SURE level-dependent attenuation degree and threshold tend to decrease when the resolution level increase (see Table 4), -
(iii)
for every fixed
 , the variance of the optimal SURE parameters over the 25 noise realizations is small; optimal parameters are not very disturbed for different noise realizations,
, the variance of the optimal SURE parameters over the 25 noise realizations is small; optimal parameters are not very disturbed for different noise realizations, -
(iv)
as far as the level dependent strategy is concerned, the attenuation degree as well as the threshold tends to decrease when the resolution level increases for a fixed
 .
.
4. Smooth Adaptation
In this section, we highlight specific features of SigShrink functions with respect to several issues in image processing.
Besides its simplicity (function with explicit close form, in contrast to parametric methods such as Bayesian shrinkages [9–14]), the main features of the SigShrink functions in image processing are the following.
Adjustable Denoising
The flexibility of the SigShrink parameters allows to choose the denoising level. From hard denoising (degenerated SigShrink) to smooth denoising, there exists a wide class of regularities that can be attained for the denoised signal by adjusting the attenuation degree and threshold.
Artifact-Free Denoising
The smoothness of the nondegenerated SigShrink functions allows for reducing noise without impacting significantly the signal; a better preservation of the signal characteristics (visual perception) and its statistical properties is guaranteed due to the fact that the shrinkage is performed with less variability among coefficients with close values.
Contrast Function
The SigShrink function and its inverse, the SigStretch function, can be seen as contrast functions. The SigShrink function enhances contrast, whereas the SigStretch function reduces contrast.
In what follows, we detail these characteristics. The following proposition characterizes the SigStretch function.
Proposition 4.1.
The SigStretch function, denoted  , is defined as the inverse of the SigShrink function
, is defined as the inverse of the SigShrink function  and is given by
and is given by

for any real value  , with
, with  being the Lambert function defined as the inverse of the function:
being the Lambert function defined as the inverse of the function:  .
.
Proof.
[See appendix].
In the rest of the paper, the wavelet transform used is the Stationary (also call shift-invariant or redundant) Wavelet Transform (SWT) [15]. This transform has appreciable properties in denoising. Its redundancy makes it possible to reduce residual noise due to the translation sensitivity of the orthonormal wavelet transform.
4.1. Adjustable and Artifact-Free Denoising
The shrinkage performed by the SigShrink method is adjustable via the attenuation degree  and the threshold
and the threshold  .
.
Figures 4 and 5 give denoising examples for different values of  and
and  . The denoising concerns the "Lena" image corrupted by AWGN with standard deviation
. The denoising concerns the "Lena" image corrupted by AWGN with standard deviation  (Figure 3). The "Haar" wavelet and 4 decomposition levels are used for the wavelet representation (SWT). The classical minimax and universal thresholds [4] are used. In these figures,
(Figure 3). The "Haar" wavelet and 4 decomposition levels are used for the wavelet representation (SWT). The classical minimax and universal thresholds [4] are used. In these figures,  stands for the SigShrink function which parameters are
stands for the SigShrink function which parameters are  and
and  .
.
SWT SigShrink denoising of "Lena" image corrupted by AWGN with standard deviation  . The universal threshold
. The universal threshold  and the minimax threshold
and the minimax threshold  are used. The universal threshold (the larger threshold) yields a smoother denoising, whereas the minimax threshold leads to better preservation of the textural information contained in the image.
are used. The universal threshold (the larger threshold) yields a smoother denoising, whereas the minimax threshold leads to better preservation of the textural information contained in the image.





Zoom of the SigShrink denoising of "Lena" images of Figure 4.
For a fixed attenuation degree, we observe that the smoother denoising is obtained with the larger threshold (universal threshold). Small value for the threshold (minimax threshold) leads to better preservation of the textural information contained in the image (compare in Figure 4, image (a) versus image (d); image (b) versus image (e); image (c) versus image (f); or equivalently, compare the zooms of these images shown in Figure 5).
Now, for a fixed threshold  , the SigShrink shape is controllable via
, the SigShrink shape is controllable via (see Figure 2). The attenuation degree
(see Figure 2). The attenuation degree  , reflects the regularity of the shrinkage and the attenuation imposed to data with small amplitudes (mainly noise coefficients). The larger
, reflects the regularity of the shrinkage and the attenuation imposed to data with small amplitudes (mainly noise coefficients). The larger  , the more the noise reduction. However, SigShrink functions are more regular for small values of
, the more the noise reduction. However, SigShrink functions are more regular for small values of  , and thus, small values for
, and thus, small values for  lead to less artifacts (in Figure 5, compare images 5(d), 5(e), and 5(f)).
lead to less artifacts (in Figure 5, compare images 5(d), 5(e), and 5(f)).
It follows that SigShrink denoising is flexible thanks to parameters  and
and  , preserves the image features, and leads to artifact-free denoising. It is thus possible to reduce noise without impacting the signal characteristics significantly. Artifact free denoising is relevant in many applications, in particular for medical imagery where visual artifacts must be avoided. In this respect, we henceforth consider small values for the attenuation degree.
, preserves the image features, and leads to artifact-free denoising. It is thus possible to reduce noise without impacting the signal characteristics significantly. Artifact free denoising is relevant in many applications, in particular for medical imagery where visual artifacts must be avoided. In this respect, we henceforth consider small values for the attenuation degree.
Note that the SURELET "sum of DOGs" parameterization does not allow for such a heuristically adjustable denoising because the physical interpretation of its parameters is not explicit, whereas the SigShrink and the standard hard, soft, NNG, and SCAD thresholding functions mentioned in Section 3.1 depend on parameters with more intuitive physical meaning (threshold height and an additional attenuation degree parameter for SigSghink). Denoising examples achieved by using the hard, soft, NNG, and SCAD thresholding functions are given in Figure 6, for a comparison with the SigShrink denoising. The minimax threshold is used for the denoising (the results are even worse with the universal threshold). As can be seen in this figure, artifacts are visible in the image denoised by using hard thresholding, whereas images denoised by using soft, NNG, and SCAD thresholding functions tend to be over smoothed. Numerical comparison of the denoising PSNRs performed by SigShrink and these standard thresholding functions can be found in [1].
Denoising examples by using standard thresholding functions. The “Haar” wavelet and 4 decomposition levels are used for the wavelet representation (SWT). The denoising concerns the image of Figure 3.
Remark 3.2.
At this stage, it is worth mentioning the following. Some parametric shrinkages using a priori distributions for modeling the signal wavelet coefficients can sometimes be described by nonparametric functions with explicit formulas (e.g., a Laplacian assumption leads to a soft-thresholding shrinkage). In this respect, one can wonder about possible links between SigShrink and the Bayesian Sigmoid Shrinkage (BSS) of [14]. BSS is a one-parameter family of shrinkage functions; whereas SigShrink functions depend on two parameters. Fixing one of these two parameters yields a subclass of SigShrink functions. It is then reasonable to think that depending on the distribution of the signal and noise wavelet coefficients, these functions should somehow relate to BSS. Actually, such a possible link has not yet been established.
To conclude this section, note that shrinkages and regularization procedures are linked in the sense that a shrinkage function solves to a regularization problem constrained by a specific penalty function [16]. Since SigShrink functions satisfy assumptions of [16, Proposition 3.2], the shrinkage obtained by using a function  can be seen as a regularization approximation [7] by seeking the vector
can be seen as a regularization approximation [7] by seeking the vector  that minimizes the penalized least squares
that minimizes the penalized least squares

where  is the penalty function associated with
is the penalty function associated with  is defined for every
is defined for every  by
by

with  being the SigStretch function (inverse of the SigShrink function
being the SigStretch function (inverse of the SigShrink function  , see (11)). Thus, SigShrink has several interpretations depending on the model used.
, see (11)). Thus, SigShrink has several interpretations depending on the model used.
4.2. Speckle Denoising
In SAR, oceanography and medical ultrasonic imagery, sensors record many gigabits of data per day. These images are mainly corrupted by speckle noise. If postprocessing such as segmentation or change detection have to be performed on these databases, it is essential to be able to reduce speckle noise without impacting the signal characteristics significantly. The following illustrates that SigShrink makes it possible to achieve this because of its flexibility (see the shapes of SigShrink functions given in Figure 2) and the artifact-free denoising they perform (see Figures 4 and 5). In addition, since SigShrink is invertible, it is not essential to store a copy of the original database (thousands and thousands of gigabits recorded every year); one can retrieve an original image by simply applying the inverse SigShrink denoising procedure (SigStrech functions). More precisely, the following illustrates that SigShrink performs well for denoising speckle noise in the wavelet domain.
Speckle noise is a multiplicative type noise inherent to signal acquisition systems using coherent radiation. This multiplicative noise is usually modeled as a correlated stationary random process independent of the signal reflectance.
Two different additive representations are often used for speckle noise. The first model is a "signal-dependent" stationary noise model; noise, assumed to be stationary, depends on the signal reflectance. This model is simply obtained by noting that  , with
, with  being the signal reflectance and
being the signal reflectance and  being a stationary random process independent of
being a stationary random process independent of  . The second model is a "signal-independent" model obtained by applying a logarithmic transform to the noisy image.
. The second model is a "signal-independent" model obtained by applying a logarithmic transform to the noisy image.
We begin with the speckle signal-dependent model. The denoising procedure then involves applying an SWT to the noisy image, estimating the noise standard deviation in each SWT subband by the robust Median of the Absolute Deviation ((MAD), normalized by the constant 0.6745) estimator [4], shrinking the wavelet coefficients by using a SigShrink function adjusted with the minimax threshold [4], and reconstructing an estimate of the signal by means of the inverse SWT. The results obtained for the "Lena" image corrupted by speckle noise (Figure 7(a)) are shown in Figures 7(b) and 7(c).
SigShrink denoising of the "Lena" image corrupted by speckle noise. The SWT with four resolution levels and the Haar filters are used. The noise standard deviation is estimated by the MAD normalized by the constant 0.6745 (see [4]).
In addition, we consider the speckle signal-independent model. We use the estimation procedure described above for denoising the logarithmic transformed noisy image. The results are given in Figures 7(d) and 7(e).
By comparing the results of Figure 7, we observe that the PSNRs achieved are of the same order whatever the model. However, the denoising obtained with the additive independent noise model (logarithmic transform) has a better visual quality than that obtained with the additive signal-dependent speckle model. In fact, one can note, from this figure, the ability of SigShrink functions to reduce speckle noise without impacting structural features and textural information of the image. Note also the gain in PSNR is larger than 10 dBs, performance of the same order as that of the best up-to-date speckle denoising techniques ([17–22] among others).
4.3. Contrast Function
To conclude this section, we now present the SigShrink and SigStretch functions as contrast functions. Contrast functions are very useful in medical image processing. As a matter of fact, medical monitoring for arthroplasty (replacement of certain bone surfaces by implants due to lesions of the articular surfaces) requires 2D-3D registration of the implant, and thus, requires knowing exactly the position of the implant contour. Precise edge detection is no easy task [23] because edge detection methods are sensitive to contrast (global contrast for the image and local contrast around a contour). The following briefly describes how to use SigShrink-SigStretch functions as contrast functions.
The SigShrink function applies a penalized shrinkage to data with small amplitudes. The smaller the data amplitude, the higher the attenuation imposed by the SigShrink function. Thus, a SigShrink function is a contrast enhancing function; this function increases the gap between large and small values for the pixels of an image. As a consequence, a SigStretch function reduces the contrast by lowering the variation between large and small pixel values in the image. Figure 8 gives the original "Lena" image as well as the SigShrink  and SigStretch
and SigStretch  shrunken images. This figure highlights that the contrast of the image can be smoothly adjusted (enhancement, reduction) by applying SigShrink and SigStretch functions without introducing artifacts. Note that, as for denoising, SigShrink allows for choosing the attenuation degree imposed to the data, when the threshold height is fixed. Figure 9 illustrates the variability that can be attained by varying the SigShrink attenuation degree for enhancing the contrast of a fluoroscopic image.
shrunken images. This figure highlights that the contrast of the image can be smoothly adjusted (enhancement, reduction) by applying SigShrink and SigStretch functions without introducing artifacts. Note that, as for denoising, SigShrink allows for choosing the attenuation degree imposed to the data, when the threshold height is fixed. Figure 9 illustrates the variability that can be attained by varying the SigShrink attenuation degree for enhancing the contrast of a fluoroscopic image.
To conclude this section, we now illustrate the combination of SigShrink denoising and contrast enhancement for an ultrasonic image of breast cancer. The combination involves denoising the image by using the SigShrink method in the wavelet domain. A SigShrink function is then applied to the denoised image to enhance its contrast. The results are presented in Figure 10. It is shown that SigShrink denoises the image and preserves feature information without introducing artifacts. The parameter  is chosen so as to avoid visual artifacts. Different thresholds are experimented to highlight how we can progressively reduce noise without affecting the image textural information. The threshold
is chosen so as to avoid visual artifacts. Different thresholds are experimented to highlight how we can progressively reduce noise without affecting the image textural information. The threshold  is the detection threshold of [8]. This threshold is smaller than the minimax threshold. It is close to
is the detection threshold of [8]. This threshold is smaller than the minimax threshold. It is close to  when the sample size is large.
when the sample size is large.
SigShrink denoising for an ultrasonic image of breast cancer. The SWT with four resolution levels and the biorthogonal spline wavelet with order 3 for decomposition and with order 1 for reconstruction ("bior1.3" in Matlab Wavelet toolbox) are used. The noise standard deviation is estimated by the MAD normalized by the constant 0.6745 (see [4]).
5. Conclusion
This work proposes the use of SigShrink-SigStretch functions for practical engineering problems such as image denoising, image restoration, and image enhancement. These functions perform adjustable adaptation of data in the sense that they can enhance or reduce the variability among data, the adaptation process being regular and invertible. Because of the smoothness of the function used (infinitely differentiable in  ), the data adaptation is performed with little variability so that the signal characteristics are better preserved. The SigShrink and SigStretch methods are simple and flexible in the sense that the parameters of these classes of functions allow for a fine tuning of the data adaptation. This adaptation is nonparametric because no prior information about the signal is taken into account. A SURE-based optimization of the parameters is possible.
), the data adaptation is performed with little variability so that the signal characteristics are better preserved. The SigShrink and SigStretch methods are simple and flexible in the sense that the parameters of these classes of functions allow for a fine tuning of the data adaptation. This adaptation is nonparametric because no prior information about the signal is taken into account. A SURE-based optimization of the parameters is possible.
The denoising achieved by a SigShrink function is almost artifact-free due to the little variability introduced among data with close amplitudes. This artifact-free denoising is relevant for many applications, in particular for medical imagery where visual artifacts must be avoided. In addition, a fine calibration of SigShrink parameters allows noise reduction without impacting the signal characteristics. This is important when some postprocessing (such as a segmentation) must be performed on the signal estimate.
As far as perspectives are concerned, we can reasonably expect to improve SigShrink denoising performance by introducing interscale or/and intrascale predictor, which could provide information about the position of significant wavelet coefficients. It could also be relevant to undertake a complete theoretical and experimental comparison between SigShrink and Bayesian sigmoid shrinkage [14].
In addition, application of SigShrink to speech processing could also be considered. Since SigShrink yields denoised images that are almost artifact-free, would it be possible that such an approach denoises speech signals corrupted by AWGN without returning musical noise, in contrast to classical shrinkages using thresholding rules?
Another perspective is the SigShrink-SigStretch calibration of contrast in order to improve edge detection in medical imagery. Exact edge detection is necessary for 2D-3D registration of images. Subpixel measurement of edge is possible by using, for example, the moment-based method of [24]. However, the method is very sensible to contrast. Low contrast varying images result in multiple contours; whereas high varying contrast in image leads to good precision for certain contour points but induces lack of detection for points in lower contrast zones. The idea is the use of the SigShrink-SigStretch functions for improving image contrast so as to alleviate edge detection in medical imagery. For instance, we can expect that combining SigShrink-SigStretch with edge detection methods such as [24] can lead to good subpixel measurement of the contour in an image.
Appendix
Proof of Proposition 4.1
Because  is antisymmetric,
is antisymmetric,  has the form
has the form

for every real value  and where
and where  is such that
is such that

Therefore,  for any real value
for any real value  . We thus have
. We thus have

which is also equivalent to

It follows that

which leads to

for  . The result then follows from (A.1), (A.6), and the fact that
. The result then follows from (A.1), (A.6), and the fact that  since
since  .
.
References
Atto AM, Pastor D, Mercier G: Smooth sigmoid wavelet shrinkage for non-parametric estimation. Proceedings of the IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP '08), March-April 2008, Las Vegas, Nev, USA 3265-3268.
Stein C: Estimation of the mean of a multivariate normal distribution. The Annals of Statistics 1981, 9: 1135-1151. 10.1214/aos/1176345632
Luisier F, Blu T, Unser M: A new sure approach to image denoising: interscale orthonormal wavelet thresholding. IEEE Transactions on Image Processing 2007,16(3):593-606.
Donoho DL, Johnstone IM: Ideal spatial adaptation by wavelet shrinkage. Biometrika 1994,81(3):425-455. 10.1093/biomet/81.3.425
Bruce AG, Gao H-YE: Understanding waveshrink: variance and bias estimation. Biometrika 1996,83(4):727-745. 10.1093/biomet/83.4.727
Gao H-Y: Wavelet shrinkage denoising using the non-negative garrote. Journal of Computational and Graphical Statistics 1998,7(4):469-488. 10.2307/1390677
Antoniadis A, Fan J: Regularization of wavelet approximations. Journal of the American Statistical Association 2001,96(455):939-955. 10.1198/016214501753208942
Simoncelli EP, Adelson EH: Noise removal via bayesian wavelet coring. Proceedings of the IEEE International Conference on Image Processing (ICIP '96), September 1996, Lausanne, Switzerland 1: 379-382.
Do MN, Vetterli M: Wavelet-based texture retrieval using generalized Gaussian density and Kullback-Leibler distance. IEEE Transactions on Image Processing 2002,11(2):146-158. 10.1109/83.982822
Şendur L, Selesnick IW: Bivariate shrinkage functions for wavelet-based denoising exploiting interscale dependency. IEEE Transactions on Signal Processing 2002,50(11):2744-2756. 10.1109/TSP.2002.804091
Portilla J, Strela V, Wainwright MJ, Simoncelli EP: Image denoising using scale mixtures of Gaussians in the wavelet domain. IEEE Transactions on Image Processing 2003,12(11):1338-1351. 10.1109/TIP.2003.818640
Johnstone IM, Silverman BW: Empirical bayes selection of wavelet thresholds. Annals of Statistics 2005,33(4):1700-1752. 10.1214/009053605000000345
ter Braak CJF: Bayesian sigmoid shrinkage with improper variance priors and an application to wavelet denoising. Computational Statistics and Data Analysis 2006,51(2):1232-1242. 10.1016/j.csda.2006.06.011
Coifman RR, Donoho DL: Translation Invariant de-Noising, Lecture Notes in Statistics. Springer, New York, NY, USA; 1995.
Xie H, Pierce LE, Ulaby FT: SAR speckle reduction using wavelet denoising and markov random field modeling. IEEE Transactions on Geoscience and Remote Sensing 2002,40(10):2196-2212. 10.1109/TGRS.2002.802473
Argenti F, Alparone L: Speckle removal from SAR images in the undecimated wavelet domain. IEEE Transactions on Geoscience and Remote Sensing 2002,40(11):2363-2374. 10.1109/TGRS.2002.805083
Achim A, Tsakalides P, Bezerianos A: SAR image denoising via bayesian wavelet shrinkage based on heavy-tailed modeling. IEEE Transactions on Geoscience and Remote Sensing 2003,41(8):1773-1784. 10.1109/TGRS.2003.813488
Argenti F, Bianchi T, Alparone L: Multiresolution MAP despeckling of SAR images based on locally adaptive generalized Gaussian pdf modeling. IEEE Transactions on Image Processing 2006,15(11):3385-3399.
Achim A, Kuruoglu EE, Zerubia J: SAR image filtering based on the heavy-tailed Rayleigh model. IEEE Transactions on Image Processing 2006,15(9):2686-2693.
Sen D, Swamy MNS, Ahmad MO: Computationally fast techniques to reduce AWGN and speckle in videos. IET Image Processing 2007,1(4):319-334. 10.1049/iet-ipr:20060299
Antoniadis A: Wavelet methods in statistics: some recent developments and their applications. Statistics Surveys 2007, 1: 16-55. 10.1214/07-SS014
Mahfouz MR, Hoff WA, Komistek RD, Dennis DA: Effect of segmentation errors on 3D-to-2D registration of implant models in X-ray images. Journal of Biomechanics 2005,38(2):229-239. 10.1016/j.jbiomech.2004.02.025
Atto AM, Pastor D, Mercier G: Detection threshold for non-parametric estimation. Signal, Image and Video Processing 2008,2(3):207-223. 10.1007/s11760-008-0051-x
Lyvers EP, Mitchell OR, Akey ML, Reeves AP: Subpixel measurements using a moment-based edge operator. IEEE Transactions on Pattern Analysis and Machine Intelligence 1989,11(12):1293-1309. 10.1109/34.41367
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Atto, A.M., Pastor, D. & Mercier, G. Smooth Adaptation by Sigmoid Shrinkage. J Image Video Proc 2009, 532312 (2009). https://doi.org/10.1155/2009/532312
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2009/532312

 in the positive half plan. The points
in the positive half plan. The points  and
and  represented on this graph are such that
represented on this graph are such that  and
and  is the intersection between the abscissa axis and the tangent to
is the intersection between the abscissa axis and the tangent to  at point
at point  .
.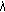 and angle
and angle 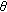 of the SigShrink function, with
of the SigShrink function, with  and
and  . Keep in mind that the larger
. Keep in mind that the larger  , the stronger the attenuation,
, the stronger the attenuation, from (4),
from (4), defined by (1).
defined by (1).
 :
:
 for the continuous (blue) curve,
for the continuous (blue) curve,
 for the dotted (red) curve, and
for the dotted (red) curve, and
 for the dashed (magenta) curve.
for the dashed (magenta) curve.
 ,
, , the SURE level-dependent attenuation degree and threshold tend to decrease when the resolution level increase (see Table
, the SURE level-dependent attenuation degree and threshold tend to decrease when the resolution level increase (see Table  , the variance of the optimal SURE parameters over the 25 noise realizations is small; optimal parameters are not very disturbed for different noise realizations,
, the variance of the optimal SURE parameters over the 25 noise realizations is small; optimal parameters are not very disturbed for different noise realizations, .
.
 , which corresponds to an input
, which corresponds to an input  dB.
dB.




 Original image
Original image



