- Research Article
- Open access
- Published:
Modeling and Visualization of Human Activities for Multicamera Networks
EURASIP Journal on Image and Video Processing volume 2009, Article number: 259860 (2009)
Abstract
Multicamera networks are becoming complex involving larger sensing areas in order to capture activities and behavior that evolve over long spatial and temporal windows. This necessitates novel methods to process the information sensed by the network and visualize it for an end user. In this paper, we describe a system for modeling and on-demand visualization of activities of groups of humans. Using the prior knowledge of the 3D structure of the scene as well as camera calibration, the system localizes humans as they navigate the scene. Activities of interest are detected by matching models of these activities learnt a priori against the multiview observations. The trajectories and the activity index for each individual summarize the dynamic content of the scene. These are used to render the scene with virtual 3D human models that mimic the observed activities of real humans. In particular, the rendering framework is designed to handle large displays with a cluster of GPUs as well as reduce the cognitive dissonance by rendering realistic weather effects and illumination. We envision use of this system for immersive visualization as well as summarization of videos that capture group behavior.
1. Introduction
Multicamera networks are becoming increasingly prevalent for monitoring large areas such as buildings, airports, shopping complexes, and even larger areas such as universities and cities. Systems that cover such immense areas invariably use a large number of cameras to provide a reasonable coverage of the scene. In such systems, modeling and visualization of human movements sensed by the cameras (or other sensors) becomes extremely important.
There exist a range of methods of varying complexity for visualization of surveillance and multicamera data. These include simple indexing methods that label events of interests for easy retrieval to virtual environments that artificially render the events in the scene. Underlying the visualization engine are systems and algorithms to extract information and events of interest. In many ways, the choice of the visualization scheme is deeply tied to the capabilities of these algorithms. As an example, a very highly accurate visualization of a human action needs motion capture algorithms that extract the location and angles of the various joints and limbs of the body. Similarly, detecting and classifying events of interest is necessary to index events of interest. Hence, an appropriate visualization of surveillance data goes hand-inhand with the specifics of the preprocessing algorithms. Towards this end, in this paper, we propose a system that is comprised of three components (see Figure 1). As the front-end, we have a multicamera tracking system that detects and estimates trajectories of moving humans. Sequences of silhouettes extracted from each human are matched against models of known activities. Information of the estimated trajectories and the recognized activities at each time instant is then presented to a rendering engine that animates a set of virtual actors synthesizing the events in the scene. In this way, the visualization system allows for seamless integration of all the information inferred from the sensed data (which could be multimodal). Such an approach places the end user in the scene, providing tools to observe the scene in an intuitive way, capturing geometric as well as spatiotemporal contextual information. Finally, in addition to visualization of surveillance data, the system also allows for modeling and analysis of activities involving multiple humans exhibiting coordinated group behavior such as in football games and training drills for security enforcement.
The outline of the proposed system. Inputs from multiple cameras are used to localize the humans in the 3D world. The observations associated with each moving human are used to recognize the performed activity by matching over a template of models learned a priori. Finally, the scene is recreated using virtual view rendering.
1.1. Prior Art
There exist simple tools that index the surveillance data for efficient retrieval of events [1, 2]. This could be coupled with simple visualization devices that alert the end user to events as they occur. However, such approaches do not present a holistic view of the scene and do not capture the geometric relationships among views and spatiotemporal contextual information in events involving multiple humans.
When a model of the scene is available, it is possible to project images or information extracted from them over the model. The user is presented with a virtual environment to visualize the events, wherein the geometric relationship between events is directly encoded by their spatial locations with respect to the scene model. Depending on the scene model and the information that is presented to the user, there exist many ways to do this. Kanade et al. [3] overlay trajectories from multiple video cameras onto a top view of the sensed region. In this context, 3D site models, if available are useful devices, as they give the underlying inference algorithms richer description of the scene as well as provide realistic visualization schemes. While such models are assumed to be known a priori, there do exist automatic modeling approaches that acquire 3D models of a scene using a host of sensors, including multiple video cameras (providing stereo), inertial and GPS sensors [4]. For example, Sebe et al. [5] present a system that combines site models with image-based rendering techniques to show dynamic events in the scene. Their system consists of algorithms which track humans and vehicles on the image plane of the camera and which render the tracked templates over the 3D scene model. The presence of the 3D scene model allows the end user the freedom to ingest local context, while viewing the scene from arbitrary points of view. However, projection of 2D templates on sprites do not make for realistic depiction of humans or vehicles.
Associated with 3D site models is also the need to model and render humans and vehicles in high resolution. Kanade and Narayanan [6] describe a system for digitizing dynamic events using multiple cameras and rendering them in virtual reality. Carranza et al. [7] present the concept of free-viewpoint video that captures the human body motion parameters from multiple synchronized video streams. The system also captures textural maps for the body surfaces using the multiview inputs and allows the human body to be visualized from arbitrary points of view. However, both systems use highly specialized acquisition frameworks that use very precisely calibrated and time-synchronized cameras acquiring high resolution images. A typical surveillance setup cannot scale up to the demanding acquisition requirements of such motion capture techniques.
Visualization of unstructured image datasets is another related topic. The Atlanta 4D Cities project [8, 9] presents a novel scheme for visualizing the time evolution of the city from unregistered photos of key landmarks of the city taken over time. The Photo Tourism project [10] is another example of visualization of a scene from a large collection of unstructured images.
Data acquired from surveillance cameras is usually not suited for markerless motion capture. Typically, the precision in calibration and time synchrony required for creating visual hulls or similar 3D constructs (a key step in motion capture) cannot be achieved easily in surveillance scenarios. Further, surveillance cameras are set up to cover a larger scene with targets in its far field. At the same time, image-based rendering approaches for visualizing data do not scale up in terms of resolution or realistic rendering when the viewing angle changes. Towards this end, in this paper we propose an approach to recognize human activities using video data from multiple cameras, and cuing 3D virtual actors to reenact the events in the scene based on the estimated trajectories and activities for each observed human. In particular, our visualization scheme relies on virtual actors performing the activities, thereby eliminating the need for acquiring detailed descriptions of humans and the pose. This reduces the computational requirements of the processing algorithms significantly, at the cost of a small loss in the fidelity of the visualization. The preprocessing algorithms are limited to localization and activity recognition, both of which are possible with low resolution surveillance cameras. Most of the modeling of visualization of activities is done offline, thereby making the rendering engine capable of meeting real-time rendering requirements.
The paper is organized as follows. The multicamera localization algorithm for estimating trajectories of moving humans with respect to the scene models is described in Section 2. Next, in Section 3 we analyze the silhouettes associated with each of the trajectories to identify the activities performed by the humans. Finally, Section 4 describes the modeling, rendering, and animation of virtual actors for visualization of the sensed data.
2. Localization in Multicamera Networks
In this section, we describe a multiview, multitarget tracking algorithm to localize humans as they walk through a scene. We work under the assumption that a scene model is available. In most urban scenes, planar surfaces (such as roads, parking lots, buildings, and corridors) are abundant especially in regions of human activity. Our tracking algorithm exploits the presence of a scene plane (or a ground plane). The assumption of the scene plane allows us to map points on the image plane of the camera uniquely to a point on the scene plane if the camera parameters (internal parameters and external parameters with respect to scene model) are known. We first describe a formal description of the properties induced by the scene plane.
2.1. Image to Scene Plane Mapping
In most urban scenes a majority of the actions in the world occur over the ground plane. The presence of a scene plane allows us to uniquely map a point from the image plane of a camera to the scene. This is possible by intersecting the preimage of the image plane point with the scene plane (see Figure 2). The imaging equation becomes invertible when the scene is planar. We exploit this invertibility to transform image plane location estimates to world plane estimates, and fuse multiview estimates of an object's location in world coordinates.
Consider views A and B (camera centers C A and C B ) of a scene with a point x imaged as u A and u B on the two views. Without any additional assumptions, given u A , we can only constrain to lie along the image of the preimage of u A (a line). However, if world was planar (and we knew the relevant calibration information) then we can uniquely invert u A to obtain x, and reproject x to obtain u B .
The mapping from image plane coordinates to a local coordinate system on the plane is defined by a projective transformation [11]. The mapping can be compactly encoded by a  matrix
matrix  such that a point
such that a point  observed on the camera can be mapped to a point
observed on the camera can be mapped to a point  in a plane coordinate system as
in a plane coordinate system as

where  is the
is the  th row of the matrix
th row of the matrix  and "tilde'' is used to denote a vector concatenated with the scalar
and "tilde'' is used to denote a vector concatenated with the scalar  . In a multicamera scenario, the projective transformation between each camera and the world plane is different. Hence, the mapping from the individual image planes to the world planes is given by a set of matrices
. In a multicamera scenario, the projective transformation between each camera and the world plane is different. Hence, the mapping from the individual image planes to the world planes is given by a set of matrices  , with
, with  defining the projective transformation for the
defining the projective transformation for the  th camera.
th camera.
2.2. Multiview Tracking
Multicamera tracking in the presence of ground-plane constraint has been the focus of many recent papers [12–15]. The two main issues that concern multiview tracking are association of data across views and using temporal continuity to track objects. Data association can be done by exploiting the ground plane constraint suitably. Various features extracted from individual views can be projected onto the ground plane and a simple consensus can be used to fuse them. Examples of such features include the medial axis of the human [14], the silhouette of the human [13], and points [12, 15]. Temporal continuity can be explored in various ways, including dynamical systems such as Kalman [16] and Particle filters [17] or using temporal graphs that emphasize spatiotemporal continuity.
We formulate a discrete time dynamical system for location tracking on the plane. The state space for each target is comprised of its location and velocity on the ground plane. Let  be the state space at time
be the state space at time  ,
,  . The state evolution equations are defined using a constant velocity model
. The state evolution equations are defined using a constant velocity model

where  is a noise process.
is a noise process.
We use point features for tracking. At each view, we perform background subtraction to segment pixels that do not correspond to a static background. We group pixels into coherent spatial blobs, and extract one representative point for each blob that roughly corresponds to the location of the leg. These representative points are mapped onto the scene plane using the mapping between the image plane and the scene plane (see Figure 3). At this point, we use the JPDAF [18] to associate the tracks corresponding to the targets with the data points generated at each view. For efficiency, we use the Maximum Likelihood association to assign data points onto targets. At the end of the data association step, let  be the data associated with the track of a target, where
be the data associated with the track of a target, where  is the projected observation from the
is the projected observation from the  th view that associates with the track.
th view that associates with the track.
Use of geometry in multiview detection: (a) snapshot from each view, (b) object free background image, (c) background subtraction results, (d) synthetically generated top view of the ground plane. The bottom point (feet) of each blob is mapped to the ground plane using the image-plane to ground-plane homography. Each color represents a blob detected in a different camera view. Points of different colors very close together on the ground plane probably correspond to the same subject seen via different camera views.Video frames captured from 4 different viewsBackground images corresponding to each viewBackground subtraction results at each viewProjection of detected points onto synthetic top view of ground-plane
With this, the observation model is given as

where  is a zero mean noise process with an identity covariance matrix.
is a zero mean noise process with an identity covariance matrix.  sets the covariance matrix of the overall noise and is defined as
sets the covariance matrix of the overall noise and is defined as

where  is a
is a  matrix with zero for all entries.
matrix with zero for all entries.  is the covariance matrix associated with the transformation
is the covariance matrix associated with the transformation  , and is defined as
, and is defined as

where  , and
, and  is the Jacobian of the transformation defined in (1).
is the Jacobian of the transformation defined in (1).
The observation model in (3) is a multiview complete observer model. There are two important features that this model captures.
-
(i)
The noise properties of the observations from different views are different, and the covariances depend not only on the view, but also on the true location of the target
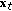 . This dependence is encoded in
. This dependence is encoded in 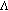 .
. -
(ii)
The MLE of
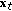 (i.e., the value of
(i.e., the value of 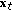 that maximizes the probability
that maximizes the probability 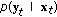 ) is a minimum variance estimator.
) is a minimum variance estimator.
Tracking of target(s) is performed using a particle filter [15]. This algorithm can be easily implemented in a distributed sensor network. Each camera transmits the blobs extracted from the background subtraction algorithm to other nodes in the network. For the purposes of tracking, it is adequate even if we approximate the blob with an enclosing bounding box. Each camera maintains a multiobject tracker filtering the outputs received from all the other nodes (along with its own output). Further, the data association problem between the tracker and the data is solved at each node separately and the association with maximum likelihood is transmitted along with data to other nodes.
3. Activity Modeling and Recognition from Multiple Views
As targets are tracked using multiview inputs, we need to identify the activity performed by them. Given that the tracking algorithm is preceded by a data association algorithm, we can analyze the activity performed by each individual separately. As targets are tracked, we associate background subtracted silhouettes with each target at each time instant and across multiple views. In the end, the activity recognition is performed using multiple sequences of silhouettes, one from each camera.
3.1. Linear Dynamical System for Activity Modeling
In several scenarios (such as far-field surveillance and objects moving on a plane), it is reasonable to model constant motion in the real world using a linear dynamic system (LDS) model on the image plane. Given  consecutive video frames
consecutive video frames  , let
, let  denote the observations (silhouette) from that frame. Then, the dynamics during this segment can be represented as
denote the observations (silhouette) from that frame. Then, the dynamics during this segment can be represented as


where  is the hidden state vector,
is the hidden state vector,  the transition matrix, and
the transition matrix, and  the measurement matrix.
the measurement matrix.  and
and  are noise components modeled as normal with
are noise components modeled as normal with  mean and covariance
mean and covariance  and
and  respectively. Similar models have been successfully applied in several tasks such as dynamic texture synthesis and analysis [19], comparing silhouette sequences [20, 21], and video summarization [22].
respectively. Similar models have been successfully applied in several tasks such as dynamic texture synthesis and analysis [19], comparing silhouette sequences [20, 21], and video summarization [22].
3.2. Learning the LTI Models for Each Segment
As described earlier, each segment is modeled as an linear time invariant (LTI) system. We use tools from system identification to estimate the model parameters for each segment. The most popular model estimation algorithms is PCA-ID [19]. PCA-ID [19] is a suboptimal solution to the learning problem. It makes the assumption that filtering in space and time are separable, which makes it possible to estimate the parameters of the model very efficiently via principal component analysis (PCA).
We briefly describe the PCA-based method to learn the model parameters here. Let observations  represent the features for the frames
represent the features for the frames  . The goal is to learn the parameters of the model given in (7). The parameters of interest are the transition matrix
. The goal is to learn the parameters of the model given in (7). The parameters of interest are the transition matrix  and the observation matrix
and the observation matrix  . Let
. Let  be the singular value decomposition of the data. Then, the estimates of the model parameters
be the singular value decomposition of the data. Then, the estimates of the model parameters  are given by
are given by  , where
, where  and
and  . These estimates of
. These estimates of  and
and  constitute the model parameters for each action segment. For the case of flow, the same estimation procedure is repeated for the
constitute the model parameters for each action segment. For the case of flow, the same estimation procedure is repeated for the  - and
- and  -components of the flow separately. Thus, each segment is now represented by the matrix pair
-components of the flow separately. Thus, each segment is now represented by the matrix pair  .
.
3.3. Classification of Actions
In order to perform classification, we need a distance measure on the space of LDS models. Several distance metrics exist to measure the distance between linear dynamic models. A unifying framework based on subspace angles of observability matrices was presented in [23] to measure the distance between ARMA models. Specific metrics such as the Frobenius norm and the Martin metric [24] can be derived as special cases based on the subspace angles. The subspace angles ( ) between the range spaces of two matrices
) between the range spaces of two matrices  and
and  are recursively defined as follows [23]:
are recursively defined as follows [23]:

subject to the constraints  and
and  for
for  . The subspace angles between two ARMA models [
. The subspace angles between two ARMA models [ ] and [
] and [ ] can be computed by the method described in [23]. Efficient computation of the angles can be achieved by first solving a discrete Lyapunov equation, for details of which we refer the reader to [23]. Using these subspace angles
] can be computed by the method described in [23]. Efficient computation of the angles can be achieved by first solving a discrete Lyapunov equation, for details of which we refer the reader to [23]. Using these subspace angles  ,
,  , three distances, Martin distance (
, three distances, Martin distance ( ), gap distance (
), gap distance ( ), and Frobenius distance (
), and Frobenius distance ( ) between the ARMA models are defined as follows:
) between the ARMA models are defined as follows:

We use the Frobenius distance in all the results shown in this paper. The distance metrics defined above cannot account for low-level transformation such as when there is a change in viewpoint or there is an affine transformation of the low-level features. We propose a technique to build these invariances into the distance metrics defined previously.
3.4. Affine and View Invariance
In our model, under feature level affine transforms or view-point changes, the only change occurs in the measurement equation and not the state equation. As described in Section 3.2 the columns of the measurement matrix ( ) are the principal components (PCs) of the observations of that segment. Thus, we need to discover the transformation between the corresponding
) are the principal components (PCs) of the observations of that segment. Thus, we need to discover the transformation between the corresponding  matrices under an affine/view change. It can be shown that under affine transformations the columns of the
matrices under an affine/view change. It can be shown that under affine transformations the columns of the  matrix undergo the same affine transformation [22].
matrix undergo the same affine transformation [22].
Modified Distance Metric
Proceeding from the above, to match two ARMA models of the same activity related by a spatial transformation, all we need to do is to transform the  matrices (the observation equation). Given two systems
matrices (the observation equation). Given two systems  and
and  we modify the distance metric as
we modify the distance metric as

where  is any of the distance metrics in (9),
is any of the distance metrics in (9),  is the transformation.
is the transformation.  . Columns of
. Columns of  are the transformed columns of
are the transformed columns of  . The optimal transformation parameters are those that achieve the minimization in (10).
. The optimal transformation parameters are those that achieve the minimization in (10).
The conditions for the above result to hold are satisfied by the class of affine transforms. For the case of homographies, the result is valid when it can be closely approximated by an affinity. Hence, this result provides invariance to small changes in view. Thus, we augment the activity recognition module by examples from a few canonical viewpoints. These viewpoints are chosen in a coarse manner along a viewing circle.
Thus, for a given set of actions  , we store a few exemplars taken from different views
, we store a few exemplars taken from different views  . After model fitting, we have the LDS parameters for
. After model fitting, we have the LDS parameters for  for action
for action  from viewing direction
from viewing direction  . Given a new video, the action classification is given by
. Given a new video, the action classification is given by

where  is given by (10).
is given by (10).
We also need to consider the effect of different execution rates of the activity when comparing two LDS parameters. In the general case, one needs to consider warping functions of the form  such as in [25] where Dynamic time warping (DTW) is used to estimate
such as in [25] where Dynamic time warping (DTW) is used to estimate  . We consider linear warping functions of the form
. We consider linear warping functions of the form  for each action. Consider the state equation of a segment:
for each action. Consider the state equation of a segment:  . Ignoring the noise term for now, we can write
. Ignoring the noise term for now, we can write  . Now, consider another sequence that is related to
. Now, consider another sequence that is related to  by
by  In the discrete case, for noninteger
In the discrete case, for noninteger  this is to be interpreted as a fractional sampling rate conversion as encountered in several areas of DSP. Then,
this is to be interpreted as a fractional sampling rate conversion as encountered in several areas of DSP. Then,  , that is, the transition matrix for the second system is related to the first by
, that is, the transition matrix for the second system is related to the first by  . Given two transition matrices of the same activity but with different execution rates, we can get an estimate of
. Given two transition matrices of the same activity but with different execution rates, we can get an estimate of  from the eigenvalues of
from the eigenvalues of  and
and  as
as

where  and
and  are the complex eigenvalues of
are the complex eigenvalues of  and
and  respectively. Thus, we compensate for different execution rates by computing
respectively. Thus, we compensate for different execution rates by computing  . After incorporating this, the distance metric becomes
. After incorporating this, the distance metric becomes

where  . To reduce the dimensionality of the optimization problem, we can estimate the time-warp factor
. To reduce the dimensionality of the optimization problem, we can estimate the time-warp factor  and the spatial transformation
and the spatial transformation  separately.
separately.
3.5. Inference from Multiview Sequences
In the proposed system, each moving human can potentially be observed from multiple cameras, generating multiple observation sequences that can be used for activity recognition (see Figure 4). While the modified distance metric defined in (10) allows for affine view invariance and homography transformations that are close to affinity, the distance metric does not extend gracefully for large changes in view. In this regard, the availability of multiview observations allow for the possibility that the pose of the human in one of the observations is in the vicinity of the pose in the training dataset. Alternatively, multiview observations reduce the range of poses over which we need view invariant matching. In this paper, we exploit multiview observations by matching each sequence independently to the learnt models and picking the activity that matches with the lowest score.
After activity recognition is performed, an index of the spatial locations of the humans and the activity that is performed over various time intervals is created. The visualization system renders a virtual scene using a static background overlaid with virtual actors animated using the indexed information.
4. Visualization and Rendering
The visualization subsystem is responsible for synthesizing the output of all of the other subsystems and algorithms and transforming them into a unified and coherent user experience. The nature of the data managed by our system leads to a somewhat unorthodox user interaction model. The user is presented with a  reconstruction of the target scenario as well as the acquired videos. The
reconstruction of the target scenario as well as the acquired videos. The  reconstruction and video streams are synchronized and are controlled by the user via the navigation system described in what follows. Many visualization systems deal with spatial data, allowing six degrees of freedom, or temporal data, allowing two degrees of freedom. However, the visualization system described here allows the user eight degrees of freedom, as they navigate the reconstruction of various scenarios.
reconstruction and video streams are synchronized and are controlled by the user via the navigation system described in what follows. Many visualization systems deal with spatial data, allowing six degrees of freedom, or temporal data, allowing two degrees of freedom. However, the visualization system described here allows the user eight degrees of freedom, as they navigate the reconstruction of various scenarios.
For spatial navigation, we employ a standard first person interface where the user can move freely about the scene. However, to allow for broader views of the current visualization, we do not restrict the user to a specific height above the ground plane. In addition to unconstrained navigation, the user may choose to view the current visualization from the vantage point of any of the cameras that were used during the acquisition process. Finally, the viewpoint may be smoothly transitioned between these different vantage points; a process made smooth and visually appealing through the use of double quaternion interpolation [26].
Temporal navigation employs a DVR-like approach. Users are allowed to pause fast forward and rewind the ongoing scenario. The  reconstruction and video display actually run in different client applications, but maintain synchronization via message passing. The choice to decouple the
reconstruction and video display actually run in different client applications, but maintain synchronization via message passing. The choice to decouple the  and
and  components of the system was made to allow for greater scalability and is discussed in more detail below.
components of the system was made to allow for greater scalability and is discussed in more detail below.
The design and implementation of the visualization system is driven by numerous requirements and desiderata. Broadly, the goals for which we aim are scalability and visual fidelity. More specifically, they can be enumerated as follows.
-
(1)
Scalability
-
(i)
system should scale well across a wide range of display devices, such as a laptop to a tiled display,
-
(ii)
system should scale to many independent movers,
-
(iii)
integration of new scenarios should be easy.
-
(i)
-
(2)
Visual fidelity
-
(i)
visual fidelity should be maximized subject to scalability and interactivity considerations,
-
(ii)
environmental effects impact user perception and should be modeled,
-
(iii)
when possible (and practical) the visualization should reflect the appearance of movers,
-
(iv)
coherence between the video and the 3D visualization mitigate cognitive dissonance, so discrepancies should be minimized.
-
(i)
4.1. Scalability and Modularity
The initial target for the visualization engine was a cluster with 15 CPU/GPU coupled display nodes. The general architecture of this system is illustrated in Figure 5(a), and an example of the system interface running on the tiled display is shown in Figure 5(b). This cluster drives a tiled display of high resolution LCD monitors with a combined resolution of  for a total of 57 million pixels. All nodes are connected by a combination Infiniband/Myrinet network as well as gigabit ethernet.
for a total of 57 million pixels. All nodes are connected by a combination Infiniband/Myrinet network as well as gigabit ethernet.
To speed development time and avoid some of the more mundane details involved in distributed visualization, we built the  component atop OpenSG [27, 28]. We meet our scalability requirement by decoupling the disparate components of the visualization and navigation system as much as possible. In particular, we decouple the renderer, which is implemented as a client application, from the user input application, which acts as a server. On the CPU-GPU cluster, this allows the user to directly interact with a control node from which the rendering nodes operate independently, but from which they accept control over viewing and navigation parameters. Moreover, we decouple the
component atop OpenSG [27, 28]. We meet our scalability requirement by decoupling the disparate components of the visualization and navigation system as much as possible. In particular, we decouple the renderer, which is implemented as a client application, from the user input application, which acts as a server. On the CPU-GPU cluster, this allows the user to directly interact with a control node from which the rendering nodes operate independently, but from which they accept control over viewing and navigation parameters. Moreover, we decouple the  visualization, which is highly interactive in nature, from the
visualization, which is highly interactive in nature, from the  visualization, which is essentially noninteractive. Each video is displayed in a separate instance of the MPlayer application. An additional client program is coupled with each MPlayer instance, which receives messages sent by the user input application over the network and subsequently controls the video stream in accordance with these messages. The decoupling of these different components serves dual goals. First, it facilitates scaling the number of systems participating in the visualization trivial. Second, reducing interdependence among components allows for superior performance.
visualization, which is essentially noninteractive. Each video is displayed in a separate instance of the MPlayer application. An additional client program is coupled with each MPlayer instance, which receives messages sent by the user input application over the network and subsequently controls the video stream in accordance with these messages. The decoupling of these different components serves dual goals. First, it facilitates scaling the number of systems participating in the visualization trivial. Second, reducing interdependence among components allows for superior performance.
This modularization extends from the design of the rendering system to that of the animation system. In fact, scenario integration is nearly automatic. Each scenario has a unique set of parameters (e.g., number of actors, actions performed, duration), and a small amount of meta-data (e.g., location of corresponding videos and animation database), and is viewed by the rendering system as a self-contained package. Figure 6(a) illustrates how each packaged scenario interacts with the geometry database, which contains models and animations for all of the activities supported by the system. The position data specifies a location, for each frame, for all of the actors tracked by the acquisition system. The scene description data contains information pertaining to the activities performed by each actor for various frame ranges as well as the temporal resolution of the acquisition devices (this latter information is needed to keep the  and
and  visualizations synchronized).
visualizations synchronized).
The requirement that the rendering system should scale to allow many actors dictates that shared data must be exploited. This data sharing works at two distinct levels. First, geometry is shared. The targets tracked in the videos are represented in the  visualization by representative proxy models, both because the synchronization and resolution of the acquisition devices prohibit stereo reconstruction, and because unique and detailed geometry for every actor would constitute too much data to be efficiently managed in our distributed system. This sharing of geometry means that the proxy models need not to be loaded separately for each actor in a scenario, thereby reducing the system and video card memory footprint. The second level at which data is shared is at the animation level. This is illustrated in Figure 6(b). Each animation consists of a set of keyframe data, describing one iteration of an activity. For example, two steps of the walking animation bring the actor back into the original position. Thus, the walking animation may be looped, while changing the actor's position and orientation, to allow for longer sequences of walking. The other animations are similarly composable. The shared animation data means that all of the characters in a given scenario who are performing the same activity may share the data for the corresponding animation. If all of the characters are jogging, for instance, only one copy of the jogging animation needs to reside in memory, and each of the performing actors will access the keyframes of this single, shared animation.
visualization by representative proxy models, both because the synchronization and resolution of the acquisition devices prohibit stereo reconstruction, and because unique and detailed geometry for every actor would constitute too much data to be efficiently managed in our distributed system. This sharing of geometry means that the proxy models need not to be loaded separately for each actor in a scenario, thereby reducing the system and video card memory footprint. The second level at which data is shared is at the animation level. This is illustrated in Figure 6(b). Each animation consists of a set of keyframe data, describing one iteration of an activity. For example, two steps of the walking animation bring the actor back into the original position. Thus, the walking animation may be looped, while changing the actor's position and orientation, to allow for longer sequences of walking. The other animations are similarly composable. The shared animation data means that all of the characters in a given scenario who are performing the same activity may share the data for the corresponding animation. If all of the characters are jogging, for instance, only one copy of the jogging animation needs to reside in memory, and each of the performing actors will access the keyframes of this single, shared animation.
4.2. Visual Fidelity
Subject to the scalability and interactivity constraints detailed above, we pursue the goal of maximizing the visual fidelity of the rendering system. Advanced visual effects serve not only to enhance the experience of the user, but often to provide necessary and useful visual cues and to mitigate distractions. Due to the scalability requirement, each geometry proxy is of relatively low polygonal complexity. However, we use smooth shading to improve the visual fidelity of the resulting rendering.
Other elements, while still visually appealing, are more substantive in what they accomplish. Shadows, for example, have a significant effect on the viewer's perception of depth and the relative locations and motions of objects in a scene [29]. The rendering of shadows has a long history in computer graphics [30]. OpenSG provides a number of shadow rendering algorithms, such as variance shadow maps [31] and percentage closer filtering shadow maps [32]. We use variance shadow maps to render shadows in our visualization, and the results can be seen in Figure 7.
Finally, the visualization system implements the rendering of a number of environmental effects. In addition to generally enhancing the visual fidelity of the reconstruction, these environmental effects serve a dual purpose. Differences between the acquired videos and the  visualization can lead the user to experience a degree of cognitive dissonance. If, for example, the acquired videos show rain and an overcast sky while the
visualization can lead the user to experience a degree of cognitive dissonance. If, for example, the acquired videos show rain and an overcast sky while the  visualization shows a clear sky and bright sun, this may distract the viewer, who is aware that the visualization and videos are meant to represent the same scene, yet they exhibit striking visual differences. In order to ameliorate this effect, we allow for the rendering of a number of environmental effects which might be present during video acquisition. Figure 8 illustrates several different environmental effects.
visualization shows a clear sky and bright sun, this may distract the viewer, who is aware that the visualization and videos are meant to represent the same scene, yet they exhibit striking visual differences. In order to ameliorate this effect, we allow for the rendering of a number of environmental effects which might be present during video acquisition. Figure 8 illustrates several different environmental effects.
5. Results
We tested the described system on the outdoor camera facility at the University of Maryland. Our testbed consists of six wall-mounted Pan Tilt Zoom cameras observing an area of roughly  . We built a static model of the scene using simple planar structures and manually aligned high resolution textures on each surface. Camera locations and calibrations were done manually by registering points on their image plane with respect to scene points and using simple triangulation techniques to obtain both their internal and external parameters. Finally, the image plane to scene plane transformation were computed by defining a local coordinate system on the ground plane and using manually obtained correspondences to compute the projective transformation linking the two.
. We built a static model of the scene using simple planar structures and manually aligned high resolution textures on each surface. Camera locations and calibrations were done manually by registering points on their image plane with respect to scene points and using simple triangulation techniques to obtain both their internal and external parameters. Finally, the image plane to scene plane transformation were computed by defining a local coordinate system on the ground plane and using manually obtained correspondences to compute the projective transformation linking the two.
5.1. Multiview Tracking
We tested the efficiency of the multicamera tracking system over a four camera system. (see Figure 9). Ground truth was obtained using markers on the plane, and manually annotating time-instants when subjects reached the markers. In our experiments, we compare two observation models, one employing the proposed approach and the other that assumes isotropic modeling across views. A particle filter was used to track, the choice motivated given missing data points due to occlusion. Testing was performed over a video of 8000 frames with three targets introduced sequentially at frames 1000, 4300, and 7200. Figure 9 shows tracking results for this experiment. The proposed model consistently results in lower KL divergence to the ground truth.
Tracking results for three targets over the 4 camera dataset. (best viewed in color/at high Zoom) (a) Snapshots of tracking output at various timestamps. (b) Evaluation of tracking using Symmetric KL divergence from ground truth. Two systems are compared: one using the proposed observation model and the other using isotropic models across cameras. Each plot corresponds to a different target. The trackers using isotropic models swap identities around frame 6000. The corresponding KL-divergence values go off scale.
Figure 10 shows localization results of nine subjects over the ground plane using inputs from six cameras. The subjects were allowed to move around freely and the multicamera algorithm described in this paper was used to track them. The use of six cameras allowed for near complete coverage of the sensed region, as well as coverage from multiple cameras in many regions. The availability of multiview observations allows us to obtain persistent tracking results even under occlusion and poor background subtraction. Finally, multiview fusion leads to robust estimate of the target location.
Output from the multiobject tracking algorithm working with input from six camera views. (a) Shows four camera views of a scene with several humans walking. Each camera independently detects/tracks the humans using a simple background subtraction scheme. The center location of the feet of each human is indicated with color-coded circles in each view. These estimates are then fused together taking into account the relationship between each view and the ground plane. (b) shows the fused trajectories overlaid on a top-down view of the ground plane.
5.2. Activity Analysis
Figure 11 shows recognition of activities of an individual performing activities using a single camera. The observation sequence obtained for this scenario was processing using a sliding window of  frames. For each window of observations, LDS parameters were estimated using the learning algorithm in Section 3.2. This is compared against the parameters of the training sequences for the various activities using the modified distance metric of (11).
frames. For each window of observations, LDS parameters were estimated using the learning algorithm in Section 3.2. This is compared against the parameters of the training sequences for the various activities using the modified distance metric of (11).
Activity recognition results over a sequence involving a single human performing various activities. (a) The two rows show the sample silhouettes from the observation sequence. Also marked in bounding boxes are detected activities: squat (in broken cyan) and jogging-in-place (dark brown). The plot in (b) shows results of activity detections over the whole video sequence. The related input and rendered sequence have been provided in the supplementary material available online at doi:10.1155/2009/259860.
We also designed recognition experiments to test the ability of our approach to handle view invariances. In this experiment, we have 10 activities—Bend, Jog, Push, Squat, Wave, Kick, Batting, Throw, Turn Sideways, Pick Phone. Each activity is executed at varying rates. For each activity, a model is learnt and stored as an exemplar. The features (flow-fields) are then translated and scaled to simulate a camera shift and zoom. Models were built on the new features, and tested using the stored exemplars. For the recognition experiment, we learnt only a single LDS model for the entire duration of the activity instead of a sequence. We also implemented a heuristic procedure in which affine transforms are compensated for by locating the center of mass of the features and building models around its neighborhood. We call it Center of Mass Heuristic (CMH). Recognition percentages are shown in Table 1. The baseline column corresponds to direct application of the Frobenius distance. We see that our method performs better in almost all cases.
5.3. Visualization
Finally, the results of localization and activity recognition are used in creating a virtual rendition of the events of the videos. Figures 12 and 13 show snapshots from the system working on the scenarios corresponding to Figures 10 and 11. We direct the reader to videos in the supplementary material that illustrate the results and the tools of the proposed system.
Visualization of the multitarget tracking results of Figure 10. (a) and (c) with each image showing snapshots from four of the six cameras. The proposed system allows for arbitrary placement of the virtual camera. We refer the reader to the supplementary material for a video sequence showcasing this result.
Rendering of activities performed in Figure 11. What is shown are snapshots of two activities as rendered by our system.
6. Conclusion
In this paper, we present a test bed for novel visualization of dynamic events of a scene by providing an end user the freedom to view the scene from arbitrary points of view. Using a sequence of localization and activity recognition algorithms we index the dynamic content of a scene. The captured information is rendered in the scene model using virtual actors along with the tools to visualize the events from arbitrary views. This allows the end user to get the geometric and spatiotemporal relationships between events and humans very intuitively. Future work involves modeling complicated activities along with the ability to make the rendered scene more faithful to the sensed imagery by suitably tailoring the models used to drive the virtual actors. Also of interest is providing a range of rendering possibilities covering image-based rendering, virtual actors and markerless motion capture methods. Such a solution would require advance in both processing algorithms (such as single view motion capture) and in rendering techniques for fast visualization.
References
Shu C-F, Hampaour A, Lu M, et al.: IBM smart surveillance system (S3): a open and extensible framework for event based surveillance. Proceedings of IEEE International Conference on Advanced Video and Signal Based Surveillance (AVSS '05), 2005 318-323.
Porikli F: Multi-camera surveillance: object-based summarization approach. MERL A Mitsubishi Electric Research Laboratory; March 2004.
Kanade T, Collins R, Lipton A, Burt P, Wixson L: Advances in cooperative multi-sensor video surveillance. Proceedings of DARPA Image Understanding Workshop, 1998 1: 3-24.
Akbarzadeh A, Frahm JM, Mordohai P, et al.: Towards urban 3D reconstruction from video. Proceedings of the 3rd International Symposium on 3D Data Processing, Visualization, and Transmission (3DPVT '06), 2006 4:
Sebe IO, Hu J, You S, Neumann U: 3D video surveillance with augmented virtual environments. In Proceedings of International Multimedia Conference, 2003, New York, NY, USA. ACM; 107-112.
Kanade T, Narayanan PJ: Virtualized reality: perspectives on 4D digitization of dynamic events. IEEE Computer Graphics and Applications 2007,27(3):32-40.
Carranza J, Theobalt C, Magnor MA, Seidel H-P: Free-viewpoint video of human actors. ACM Transactions on Graphics 2003,22(3):569-577. 10.1145/882262.882309
Schindler G, Krishnamurthy P, Dellaert F: Line-based structure from motion for urban environments. Proceedings of the 3rd International Symposium on 3D Data Processing, Visualization, and Transmission (3DPVT '06), 2006 846-853.
Schindler G, Dellaert F, Kang SB: Inferring temporal order of images from 3D structure. Proceedings of the IEEE Computer Society Conference on Computer Vision and Pattern Recognition (CVPR '07), 2007
Snavely N, Seitz SM, Szeliski R: Photo tourism: exploring photo collections in 3D. In Proceedings of the 33rd International Conference and Exhibition on Computer Graphics and Interactive Techniques (SIGGRAPH '06), July-August 2006, Boston, Mass, USA. ACM Press; 835-846.
Hartley R, Zisserman A: Multiple View Geometry in Computer Vision. Cambridge University Press, Cambridge, UK; 2003.
Fleuret F, Berclaz J, Lengagne R: Multi-camera people tracking with a probabilistic occupancy map. July 2006., (EPFL/CVLAB2006.07):
Khan SM, Shah M: A multi-view approach to tracking people in crowded scenes using a planar homography constraint. Proceedings of the 9th European Conference on Computer Vision (ECCV '06), May 2006, Graz, Austria 4: 133-146.
Kim K, Davis LS: Multi-camera tracking and segmentation of occluded people on ground plane using search-guided particle filtering. Proceedings of the 9th European Conference on Computer Vision (ECCV '06), May 2006, Graz, Austria, Lecture Notes in Computer Science 3953: 98-109.
Sankaranarayanan AC, Chellappa R: Optimal multi-view fusion of object locations. Proceedings of IEEE Workshop on Motion and Video Computing (WMVC '08), January 2008, Copper Mountain, Colo, USA 1-8.
Anderson BDO, Moore JB: Optimal Filtering. Dover, New York, NY, USA; 2005.
Doucet A, Freitas ND, Gordon N: Sequential Monte Carlo Methods in Practice. Springer, New York, NY, USA; 2001.
Bar-Shalom Y, Fortmann T: Tracking and Data Association. Academic Press, New York, NY, USA; 1988.
Soatto S, Doretto G, Wu YN: Dynamic textures. Proceedings of the 8th IEEE International Conference on Computer Vision (ICCV '01), July 2001, Vancouver, Canada 2: 439-446.
Veeraraghavan A, Roy-Chowdhury AK, Chellappa R: Matching shape sequences in video with applications in human movement analysis. IEEE Transactions on Pattern Analysis and Machine Intelligence 2005,27(12):1896-1909.
Bissacco A, Chiuso A, Ma Y, Soatto S: Recognition of human gaits. Proceedings of IEEE Computer Society Conference on Computer Vision and Pattern Recognition (CVPR '01), December 2001 2: 52-57.
Turaga P, Veeraraghavan A, Chellappa R: Unsupervised view and rate invariant clustering of video sequences. Computer Vision and Image Understanding 2009,113(3):353-371. 10.1016/j.cviu.2008.08.009
De Cock K, De Moor B: Subspace angles between ARMA models. Systems and Control Letters 2002,46(4):265-270. 10.1016/S0167-6911(02)00135-4
Martin RJ: A metric for ARMA processes. IEEE Transactions on Signal Processing 2000,48(4):1164-1170. 10.1109/78.827549
Veeraraghavan A, Chellappa R, Roy-Chowdhury AK: The function space of an activity. Proceedings of IEEE Computer Society Conference on Computer Vision and Pattern Recognition (CVPR '06), 2006 1: 959-966.
Ge QJ, Varshney A, Menon J, Chang C: Double quaternions for motion interpolation. Proceedings of the ASME Design Engineering Technical Conference, September 1998 DETC98/DFM-5755
Reiners D, Voss G, Behr J: Opensg: basic concepts. Proceedings of the 1st OpenSG Symposium (OpenSG '02), 2002, Darmstadt, Germany
Reiners D: Special issue on the OpenSG symposium and OpenSG plus. Computers & Graphics 2004,28(1):59-61. 10.1016/j.cag.2003.10.003
Kersten D, Knill DC, Mamassian P, Bulthoff I: Illusory motion from shadows. Nature 1996,379(6560):31. 10.1038/379031a0
Crow FC: Shadow algorithms for computer graphics. SIGGRAPH Computer Graphics 1977,11(2):242-248. 10.1145/965141.563901
Donnelly W, Lauritzen A: Variance shadow maps. In Proceedings of the Symposium on Interactive 3D Graphics and Games (I3D '06), 2006, New York, NY, USA. ACM; 161-165.
Brabec S, Seidel H-P: Hardware-accelerated rendering of antialiased shadows with shadow maps. In Proceedings of the International Conference on Computer Graphics, July 2001, Hong Kong Edited by: Ip HH-S, Magnenat-Thalmann N, Lau RWH, Chua T-S. 209-214.
Acknowledgment
This work was supported by DARPA Flexiview Grant HR001107C0059 and NSF CNS 04-03313.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Sankaranarayanan, A.C., Patro, R., Turaga, P. et al. Modeling and Visualization of Human Activities for Multicamera Networks. J Image Video Proc 2009, 259860 (2009). https://doi.org/10.1155/2009/259860
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2009/259860



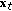 . This dependence is encoded in
. This dependence is encoded in 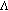 .
.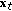 (i.e., the value of
(i.e., the value of 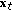 that maximizes the probability
that maximizes the probability 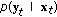 ) is a minimum variance estimator.
) is a minimum variance estimator.








