- Research Article
- Open access
- Published:
Identification of Sparse Audio Tampering Using Distributed Source Coding and Compressive Sensing Techniques
EURASIP Journal on Image and Video Processing volume 2009, Article number: 158982 (2009)
Abstract
In the past few years, a large amount of techniques have been proposed to identify whether a multimedia content has been illegally tampered or not. Nevertheless, very few efforts have been devoted to identifying which kind of attack has been carried out, especially due to the large data required for this task. We propose a novel hashing scheme which exploits the paradigms of compressive sensing and distributed source coding to generate a compact hash signature, and we apply it to the case of audio content protection. The audio content provider produces a small hash signature by computing a limited number of random projections of a perceptual, time-frequency representation of the original audio stream; the audio hash is given by the syndrome bits of an LDPC code applied to the projections. At the content user side, the hash is decoded using distributed source coding tools. If the tampering is sparsifiable or compressible in some orthonormal basis or redundant dictionary, it is possible to identify the time-frequency position of the attack, with a hash size as small as 200 bits/second; the bit saving obtained by introducing distributed source coding ranges between 20% to 70%.
1. Introduction
With the increasing diffusion of digital multimedia contents in the last years, the possibility of tampering with multimedia contents—an ability traditionally reserved, in the case of analog signals, to few people due to the prohibitive cost of the professional equipment—has become quite a widespread practice. In addition to the ease of such manipulations, the problem of the diffusion of unauthorized copies of multimedia contents is exacerbated by security vulnerabilities and peer-to-peer sharing over the Internet, where digital contents are typically distributed and posted. This is particularly true for the case of audio files, which represent the most common example of digitally distributed multimedia contents. Some versions of the same audio piece may differ from the original because of processing, due for example to compression, resampling, or transcoding at intermediate nodes. In other cases, however, malicious attacks may occur by tampering with part of the audio stream and possibly affecting its semantic content. Examples of this second kind of attacks are the alteration of a piece of evidence in a criminal trial, or the manipulation of public opinion through the use of false wiretapping. Often, for the sake of information integrity, not only it is useful to detect whether the audio content has been modified or not, but also to identify which kind of attack has been carried out. The reasons why it is generally preferred to identify how the content has been tampered with are twofold: on one hand, given an estimate of where the signal was manipulated, one can establish whether or not the audio file is still meaningful for the final user; on the other hand, in some circumstances, it may be possible to recover the original semantics of the audio file.
In the past literature, the aim of distinguishing legitimately modified copies from manipulations of a multimedia file has been addressed with two kinds of approaches: watermarks and media hashes. Both approaches have been extensively applied to the case of image content types, while fewer systems have been proposed for the case of audio signals. Digital watermarking techniques embed information directly into the media data to ensure both data integrity and authentication. Even if digital watermarks can be categorized based on several properties, such as robustness, security, complexity, and invertibility [1], a common taxonomy is to distinguish between robust and fragile watermarks. It is the latter category that is particularly useful for checking the integrity of an audio file; a fragile watermark is a mark that is easily altered or destroyed when the host data is modified through some transformation, either legitimate or not. If the watermark is designed to be robust with respect to legitimate, perceptually irrelevant modifications (e.g., compression or resampling), and at the same time to be fragile with respect to perceptually and semantic significant alterations, then it is a content-fragile watermark [1]. With this scheme, a possible tampering can be detected and localized by identifying the damage to the extracted watermark. Examples of this approach for the case of image content types are given in [2, 3]. The authors of [4] propose an image authentication scheme that is able to localize tampering, by embedding a watermark in the wavelet coefficients of an image. If a tampering occurs, the system provides information on specific frequencies and space regions of the image that have been modified. This allows the user to make application-dependent decisions concerning whether an image, which is JPEG compressed for instance, still has credibility. A similar idea, also working on the signal wavelet domain, has been applied to audio in [5], with the aim of copyright verification and tampering identification. The image watermarking system devised in [6] inserts a fragile watermark in the least significant bits of the image on a block-based fashion; when a portion of the image is tampered with, only the watermark in the corresponding blocks is destroyed, and the manipulation can be localized. Celik et al. [7] extend this method by inserting the watermark in a hierarchical way, to improve robustness against vector quantization attacks. In [8], image protection and tampering localization is achieved through a technique called "cocktail watermarking"; two complementary watermarks are embedded in the original image to improve the robustness of the detector response, while at the same time enabling tampering localization. The same ideas have been applied by the authors to the case of sounds [9], by inserting the watermark in the host audio FFT coefficients. For a more exhaustive review of audio watermarking for authentication and tampering identification see Steinebach and Dittmann [1].
Despite their widespread diffusion as a tool for multimedia protection, watermarking schemes suffer from a series of disadvantages: (1) watermarking authentication is not backward compatible with previously encoded contents (unmarked contents cannot be authenticated later by just retrieving the corresponding hash); (2) the original content is distorted by the watermark; (3) the bit rate required to compress a multimedia content might increase due to the embedded watermark. An alternative solution for authentication and tampering identification is the use of multimedia hashes. Unlike watermarks, content hashing embeds a signature of the original content as part of the header information, or can provide a hash separately from the content upon a user's request. Multimedia hashes are inspired by cryptographic digital signatures, but instead of being sensitive to single-bit changes, they are supposed to offer proof of perceptual integrity. Despite some audio hashing systems (also named audio fingerprinting) being proposed in the past few years [10–12], most of the previous research, as for the case of watermarking, has concentrated on the case of images [13, 14]. In [10], the authors build audio fingerprints by collecting and quantizing a number of robust and informative features from an audio file, with the purpose of audio identification as well as fast database lookup. Haitsma and Kalker [11] build audio fingerprints robust to legitimate content modifications (mp3 compression, resampling, moderate time, and pitch scaling), by dividing the audio signal in highly overlapping frames of about 0.3 seconds; for each frame, they compute a frequency representation of the signal through a filter bank with logarithmic spacing among the bands, in order to resemble the human auditory system (HAS). The redundance of musical sounds is exploited by taking the differences between subbands in the same frame, and between the same subbands in adjacent time instants; the resulting vector is quantized with one bit, and similarities between each short fingerprint are computed through the Hamming distance. By concatenating all the fingerprints of each frame, a global hash is obtained, which is used next to efficiently query a song database of previously encoded fingerprints. Though in principle such an approach could be used for identifying possible localized tampering in the audio stream, the authors do not explicitly address this problem. An excellent review of algorithms and applications of audio fingerprinting is presented in [12].
To the best of the authors' knowledge, no audio hashing technique has been used up to now with the purpose of detecting and localizing unauthorized audio tampering. One of the main reasons of that is probably the great amount of bits of the audio hashes required for enabling the identification of the tampering, when traditional fingerprinting approaches as the ones described above are employed. In fact, in order to limit the rate overhead, the size of the hash needs to be as small as possible. At the same time, the goal of tampering localization calls for increasing the hash size, in order to capture as much as possible about the original multimedia object. Recently, Lin et al. have proposed a new hashing technique for authentication [14] and tampering localization [15] for images, which produce very short hashes by leveraging distributed source coding theory. In this system, the hash is composed of the Slepian-Wolf encoding bitstream of a number of quantized random projections of the original image; the content user (CU) computes its own random projections on the received (and possibly tampered) image, and uses them as a side information to decode the received hash. By setting some maximum predefined tampering level on the received image (e.g., a minimum tolerated PSNR between the original and the forged image is allowed), it is possible to transmit the hash without the need of a feedback channel, performing rate allocation at the encoder side (a similar bit allocation technique has been adopted by the authors also in the context of reduced-reference image quality assessment [16]). When decoding succeeds, it is possible to identify tampered regions of the image, at the cost of additional hash bits. This scheme has been applied also to the case of audio files [17]; instead of random projections of pixels, the authors compute for each signal frame a weighted spectral flatness measure, with randomly chosen weights, and encode this information to obtain the hash. Though this scheme applies well to the authentication task (which can be attained with a hash overhead less than 100 bits/second), it is not clear how to extend the application to identification of general kinds of tampering.
We have recently proposed a new image hashing technique [18] which exploits both the distributed source coding paradigm and the recent developments in the theory of compressive sensing. The algorithm proposed in this paper extends these ideas to the scenario of audio tampering. It also shares some similarities with the works in [15, 17]; as in [17], the hash is generated by computing random projections starting from a perceptually significant time-frequency representation of the audio signal and storing the syndrome bits obtained by Low-Density Parity-Check Codes (LDPC) encoding the quantized coefficients. With respect to [17], the proposed algorithm is novel in the following aspect: by leveraging compressive sensing principles, we are able to identify tamperings that are not sparse in the time domain only, but that can be represented by a sparse set of coefficients in some orthonormal basis or redundant dictionary. Even if the spatial models introduced in [15] could be thought of as a representation of the tampering in some dictionary, it is apparent that the compressive sensing interpretation allows much more flexibility in the choice of the sparsifying basis, since it just uses off-the-shelf basis expansions (e.g., wavelet or DCT) which can be added to the system for free.
To clear up which are the capabilities and the limitations of the proposed system, Figure 1 shows an example of malicious tampering with an audio signal. This demonstration has been carried out on a piece of audio speech, with a length of approximately 2 seconds, read from a newspaper by a speaker. The whole recording, which is about 32 seconds long, has also been used as a proof of concept to present some experimental results on the system in Section 7. Figure 1(a) shows the original waveform, which corresponds to the Italian sentence "un sequestro da tredici milioni di euro" (a confiscation of thirteen million euros). This sentence has been tampered with in order to substitute the words "tredici milioni" (thirteen million) with "quindici miliardi" (fifteen billion), see Figure 1(b). In order to compute the hash, as explained in Section 4, we compute a coarse-scale perceptual time-frequency map of the signal (in this case, with a temporal resolution of  seconds). From the received tampered waveform and from the information of the hash, the user is able to identify the tampering (Figure 1(d)).
seconds). From the received tampered waveform and from the information of the hash, the user is able to identify the tampering (Figure 1(d)).
An example of the result of the proposed audio tampering identification, applied to a fragment of speech read from a newspaper. A fragment of the original audio signalTampered audio, where the words "tredici milioni" have been replaced by "quindici miliardi"A coarse-scale perceptual time-frequency map of the original signal, from which the hash signature is computedThe tampering in the perceptual time-frequency domain as estimated by the proposed algorithm
The rest of the paper is organized as follows: Section 2 provides the necessary background information about compressive sensing and distributed source coding; Section 3 describes the tampering model; Section 4 gives a detailed description of the system; Section 6 describes how it is possible to estimate the rate of the hash at the encoder without feedback channel or training; the tampering identification algorithm is tested against various kinds of attacks in Section 7, where also the different bit-rate requirements for the hash with or without distributed source coding are compared; finally, Section 8 draws some concluding remarks.
2. Background
In this section, we review the important concepts behind compressive sensing and distributed source coding, that constitute the underlying theory of the proposed tampering identification system. In spite of the relatively large amount of literature published on these fields in the past few years, this is a very concise introduction; for a more detailed and exhaustive explanation the interested reader may refer to [19–21] for compressive sensing and to [22–24] for distributed source coding.
2.1. Compressive Sampling (CS)
Compressive sampling (or compressed sensing) is a new paradigm which asserts that it is possible to perfectly recover a signal from a limited number of incoherent, nonadaptive linear measurements, provided that the signal admits a sparse representation in some orthonormal basis or redundant dictionary, that is, it can be represented by a small number of nonzero coefficients in some basis expansion. Let  be the signal to be acquired, and
be the signal to be acquired, and  , a number of linear random projections (measurements) obtained as
, a number of linear random projections (measurements) obtained as  . In general, given the prior knowledge that
. In general, given the prior knowledge that  is
is  -sparse, that is, that only
-sparse, that is, that only  out of its
out of its  coefficients are different from zero, one can recover
coefficients are different from zero, one can recover  by solving the following optimization problem:
by solving the following optimization problem:

where  simply counts the number of nonzero elements of
simply counts the number of nonzero elements of  . This program can correctly recover a
. This program can correctly recover a  -sparse signal from
-sparse signal from  random samples [25]. Unfortunately, such a problem is NP hard, and it is also difficult to solve in practice for problems of moderate size.
random samples [25]. Unfortunately, such a problem is NP hard, and it is also difficult to solve in practice for problems of moderate size.
To overcome this exhaustive search, the compressive sampling paradigm uses special measurement matrices  that satisfy the so-called restricted isometry property (RIP) of order
that satisfy the so-called restricted isometry property (RIP) of order  [21], which says that all subsets of
[21], which says that all subsets of  columns taken from
columns taken from  are in fact nearly orthogonal or, equivalently, that linear measurements taken with
are in fact nearly orthogonal or, equivalently, that linear measurements taken with  approximatively preserve the Euclidean length of
approximatively preserve the Euclidean length of  -sparse signals. This in turn implies that
-sparse signals. This in turn implies that  -sparse vectors cannot be in the null space of
-sparse vectors cannot be in the null space of  , a fact that is extremely useful, as otherwise there would be no hope of reconstructing these vectors. Merely verifying that a given
, a fact that is extremely useful, as otherwise there would be no hope of reconstructing these vectors. Merely verifying that a given  has the RIP according to the definition is combinatorially complex; however, there are well-known cases of matrices that satisfy the RIP, obtained for instance by sampling i.i.d. entries from the normal distribution with mean 0 and variance
has the RIP according to the definition is combinatorially complex; however, there are well-known cases of matrices that satisfy the RIP, obtained for instance by sampling i.i.d. entries from the normal distribution with mean 0 and variance  . When the RIP holds, then the following linear program gives an accurate reconstruction
. When the RIP holds, then the following linear program gives an accurate reconstruction

The solution of (2) is the same as the one of (1) provided that the number of measurements satisfy  , where
, where  is some small positive constant. Moreover, if
is some small positive constant. Moreover, if  is not exactly sparse, but it is at least compressible (i.e., its coefficients decay as a power law), then solving (2) guarantees that the quality of the recovered signal is as good as if one knew ahead of time the location of the
is not exactly sparse, but it is at least compressible (i.e., its coefficients decay as a power law), then solving (2) guarantees that the quality of the recovered signal is as good as if one knew ahead of time the location of the  largest values of
largest values of  and decided to measure those directly [21]. These results also hold when the signal is not sparse as is, but it has a sparse representation in some orthonormal basis. Let
and decided to measure those directly [21]. These results also hold when the signal is not sparse as is, but it has a sparse representation in some orthonormal basis. Let  denote an orthonormal matrix, whose columns are the basis vectors. Let us assume that we can write
denote an orthonormal matrix, whose columns are the basis vectors. Let us assume that we can write  , where
, where  is a
is a  -sparse vector. Clearly, (2) is a special case of this instance, when
-sparse vector. Clearly, (2) is a special case of this instance, when  is the identity matrix. Given the measurements
is the identity matrix. Given the measurements  , the signal
, the signal  can be reconstructed by solving the following problem:
can be reconstructed by solving the following problem:

Problem (3) can be solved without prior knowledge of the actual sparsifying basis  for different test bases, until a sparse reconstruction
for different test bases, until a sparse reconstruction  is obtained.
is obtained.
In most practical applications, measurements are affected by noise (e.g., quantization noise). Let us consider noisy measurements  , where
, where  is a norm-bounded noise, that is,
is a norm-bounded noise, that is,  . An approximation of the original signal
. An approximation of the original signal  can be obtained by solving the modified problem:
can be obtained by solving the modified problem:

Problem (4) is an instance of a second-order cone program (SOCP) [26] and can be solved in  time. Several fast algorithms have been proposed in the literature that attempt to find a solution to (4). In this work, we adopt the SPGL1 algorithm [27], which is specifically designed for large-scale sparse reconstruction problems.
time. Several fast algorithms have been proposed in the literature that attempt to find a solution to (4). In this work, we adopt the SPGL1 algorithm [27], which is specifically designed for large-scale sparse reconstruction problems.
2.2. Distributed Source Coding (DSC)
Consider the problem of communicating a continuous random variable  . Let
. Let  denote another continuous random variable correlated to
denote another continuous random variable correlated to  . In a distributed source coding setting, the problem is to decode
. In a distributed source coding setting, the problem is to decode  to its quantized reconstruction
to its quantized reconstruction  given a constraint on the distortion measure
given a constraint on the distortion measure  when the side information
when the side information  is available only at the decoder. Let us denote by
is available only at the decoder. Let us denote by  the rate-distortion function for the case when
the rate-distortion function for the case when  is also available at the encoder, and by
is also available at the encoder, and by  the case when only the decoder has access to
the case when only the decoder has access to  . The Wyner-Ziv theorem [23] states that, in general,
. The Wyner-Ziv theorem [23] states that, in general,  but
but  for Gaussian memoryless sources and mean square error (MSE) as distortion measure.
for Gaussian memoryless sources and mean square error (MSE) as distortion measure.
The Wyner-Ziv theorem has been applied especially in the area of video coding under the name of distributed video coding (DVC), where the source  (pixel values or DCT coefficients) is quantized with
(pixel values or DCT coefficients) is quantized with  levels, and the
levels, and the  bitplanes are independently encoded, computing parity bits by means of a turbo encoder. At the decoder, parity bits are used together with the side information
bitplanes are independently encoded, computing parity bits by means of a turbo encoder. At the decoder, parity bits are used together with the side information  to "correct"
to "correct"  into a quantized version
into a quantized version  of
of  , performing turbo decoding, typically starting from the most significant bitplanes. To this end, the decoder needs to know the joint probability density function (pdf)
, performing turbo decoding, typically starting from the most significant bitplanes. To this end, the decoder needs to know the joint probability density function (pdf)  . More recently, LDPC codes have been adopted instead of turbo codes [28, 29].
. More recently, LDPC codes have been adopted instead of turbo codes [28, 29].
Although the rate-distortion performance of a practical DSC codec strongly depends on the actual implementation employed, it is yet possible to approximately quantify the gain obtained by introducing a Wyner-Ziv coding paradigm, in order to estimate the bit saving produced in the hash signature. Let  and
and  be zero mean, i.i.d. Gaussian variables with variance, respectively,
be zero mean, i.i.d. Gaussian variables with variance, respectively,  and
and  ; also, let
; also, let  be the variance of the innovation noise
be the variance of the innovation noise  . Classical information theory [30] asserts that the rate expressed in bits per sample for a given distortion level
. Classical information theory [30] asserts that the rate expressed in bits per sample for a given distortion level  , in the case of a Gaussian source
, in the case of a Gaussian source  is given by
is given by

The rate-distortion function for the case of Wyner-Ziv encoding, when the conditions of the theorem are satisfied, is

which becomes, in the hypothesis that  , approximatively equal to the rate needed to encode the innovation
, approximatively equal to the rate needed to encode the innovation 

Subtracting (7) from (5), we obtain the expected coding gain due to Wyner-Ziv coding

As we will see in Section 4,  relates to the energy of the original signal, while
relates to the energy of the original signal, while  to the energy of the tampering. Equation (8) shows that the advantage of using a DSC approach with respect to a traditional quantization and encoding becomes consistent when the signal and the side information are well correlated, that is, when the energy of the tampering is small relative to the energy of the original sound.
to the energy of the tampering. Equation (8) shows that the advantage of using a DSC approach with respect to a traditional quantization and encoding becomes consistent when the signal and the side information are well correlated, that is, when the energy of the tampering is small relative to the energy of the original sound.
3. Tampering Model
Before describing in more detail the architecture of the system, we need to set up a model for sparse tampering. Let  be the original signal; we model the effect of a sparse tampering
be the original signal; we model the effect of a sparse tampering  as
as

where  is the modified signal received by the user. We postulate without loss of generality that
is the modified signal received by the user. We postulate without loss of generality that  has only
has only  nonzero components (in fact, it suffices for
nonzero components (in fact, it suffices for  to be sparse or compressible in some basis or frame).
to be sparse or compressible in some basis or frame).
Let  be the random measurements of the original signal and
be the random measurements of the original signal and  be the projections of the tampered signal; clearly, the relation between the tampering and the measurements is given by
be the projections of the tampered signal; clearly, the relation between the tampering and the measurements is given by

If the sensing matrix  is chosen such that it satisfies the RIP, we have that
is chosen such that it satisfies the RIP, we have that

and thus we are able to approximate the energy of the tampering from the projections computed at the decoder and the encoder-side projections reconstructed exploiting the hash. This fact comes out to be very useful to estimate the energy of the tampering at the CU side and will be exploited in Section 4. Furthermore in order to apply the Wyner-Ziv theorem, we need  to be i.i.d. Gaussian with zero mean. This has been verified through experimental simulations on several tampering examples. Indeed, a theoretical justification can be provided by invoking the central limit theorem, since each element
to be i.i.d. Gaussian with zero mean. This has been verified through experimental simulations on several tampering examples. Indeed, a theoretical justification can be provided by invoking the central limit theorem, since each element  is the sum of random variables whose statistics are not explicitly modeled.
is the sum of random variables whose statistics are not explicitly modeled.
4. Description of the System
The proposed tampering detection and localization scheme is depicted in Figure 2. The general architecture of the system is composed by two actors: on one hand, there is the content producer (CP), which is the entity that publishes or distributes the legitimate and authentic copies of the original audio content. On the other hand, there is the CU, which is the consumer of the audio content released by the CP. The CP disseminates copies of the original content  , where
, where  is the total number of audio samples of the signal, through possibly untrusted intermediaries, which may tamper with the authentic file manipulating its semantics; at the same time, the CU may get its own copy
is the total number of audio samples of the signal, through possibly untrusted intermediaries, which may tamper with the authentic file manipulating its semantics; at the same time, the CU may get its own copy  of the audio file from nodes different from the starting CP. In order to protect the integrity of the multimedia content, the CP builds a small hash signature
of the audio file from nodes different from the starting CP. In order to protect the integrity of the multimedia content, the CP builds a small hash signature  of the audio signal. To perform content authentication, the user sends a request for the hash signature to an authentication server, which is supposed to be trustworthy. By exploiting the hash, the user can estimate the distortion of the received content
of the audio signal. To perform content authentication, the user sends a request for the hash signature to an authentication server, which is supposed to be trustworthy. By exploiting the hash, the user can estimate the distortion of the received content  with respect to the original
with respect to the original  . Furthermore, if the tampering is sparse in some basis expansion, the system produces a tampering estimation
. Furthermore, if the tampering is sparse in some basis expansion, the system produces a tampering estimation  which identifies the attack in the time-frequency domain. In the following, we detail the hash generation procedure at the CP side and the tampering identification at the CU side.
which identifies the attack in the time-frequency domain. In the following, we detail the hash generation procedure at the CP side and the tampering identification at the CU side.
4.1. Generation of the Hash Signature
At the CP side, given the audio stream  and a random seed
and a random seed  , the encoder generates the hash signature
, the encoder generates the hash signature  as follows.
as follows.
(1) Frame-Based Subband Log-Energy Extraction
The original single-channel audio stream  is partitioned into nonoverlapping frames of length
is partitioned into nonoverlapping frames of length  samples. The power spectrum of each frame is subdivided into
samples. The power spectrum of each frame is subdivided into  Mel frequency subbands [31], and for each subband the related spectral log-energy is extracted. Let
Mel frequency subbands [31], and for each subband the related spectral log-energy is extracted. Let  be the energy value for the
be the energy value for the  th band at frame
th band at frame  . The corresponding log-energy value is computed as follows:
. The corresponding log-energy value is computed as follows:

The values  provide a time-frequency perceptual map of the audio signal (see Figure 1). The log-energy values are "rasterized" as a vector
provide a time-frequency perceptual map of the audio signal (see Figure 1). The log-energy values are "rasterized" as a vector  , where
, where  is the total number of log-energy values extracted from the audio stream.
is the total number of log-energy values extracted from the audio stream.
(2) Random Projections
A number of linear random projections  is produced as
is produced as  . The entries of the matrix
. The entries of the matrix  are sampled from a Gaussian distribution
are sampled from a Gaussian distribution  , using some random seed
, using some random seed  , which will be sent as part of the hash to the user.
, which will be sent as part of the hash to the user.
(3) Wyner-Ziv Encoding
The random projections  are quantized with a uniform scalar quantizer with step size
are quantized with a uniform scalar quantizer with step size  . As mentioned in Section 1, to reduce the number of bits needed to represent the hash, we do not send directly the quantization indices. Instead, we observe that the random projections computed from the possibly tampered audio signal will be available at the decoder side. Therefore, we can perform lossy encoding with side information at the decoder, where the source to be encoded is
. As mentioned in Section 1, to reduce the number of bits needed to represent the hash, we do not send directly the quantization indices. Instead, we observe that the random projections computed from the possibly tampered audio signal will be available at the decoder side. Therefore, we can perform lossy encoding with side information at the decoder, where the source to be encoded is  and the "noisy" random projections
and the "noisy" random projections  play the role of the side information. The vector
play the role of the side information. The vector  contains the log-energy values of the audio signal received at the decoder. With respect to the distributed source coding setting illustrated in Section 2.2, we have
contains the log-energy values of the audio signal received at the decoder. With respect to the distributed source coding setting illustrated in Section 2.2, we have 
 . Following the approach widely adopted in the literature on distributed video coding [24], we perform bitplane extraction on the quantization bin indices. Then each bitplane vector is LDPC coded to create the hash.
. Following the approach widely adopted in the literature on distributed video coding [24], we perform bitplane extraction on the quantization bin indices. Then each bitplane vector is LDPC coded to create the hash.
4.2. Hash Decoding and Tampering Identification
The CU receives the (possibly tampered) audio stream  and requests the syndrome bits and the random seed of the hash
and requests the syndrome bits and the random seed of the hash  from the authentication server. On each user's request, a different seed
from the authentication server. On each user's request, a different seed  is used in order to avoid that a malicious attack could exploit the knowledge of the nullspace of
is used in order to avoid that a malicious attack could exploit the knowledge of the nullspace of  [14].
[14].
-
(1)
Frame-Based Subband Log-Energy Extraction
A perceptual, time-frequency representation of the signal
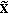 received by the CU is computed using the same algorithm described above for the CP side. At this step, the vector
received by the CU is computed using the same algorithm described above for the CP side. At this step, the vector 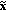 is produced.
is produced. -
(2)
Random Projections
A set of
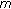 linear random measurements
linear random measurements 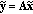 are computed using a pseudorandom matrix
are computed using a pseudorandom matrix 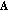 whose entries are drawn from a Gaussian distribution with the same seed
whose entries are drawn from a Gaussian distribution with the same seed 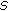 as the encoder.
as the encoder. -
(3)
Wyner-Ziv Decoding
A quantized version
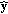 is obtained using the hash syndrome bits and
is obtained using the hash syndrome bits and 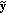 as side information. LDPC decoding is performed starting from the most significant bitplane.
as side information. LDPC decoding is performed starting from the most significant bitplane.-
(i)
If a feedback channel is available, decoding always succeeds, unless an upper bound is imposed on the maximum number of hash bits.
-
(ii)
Conversely, if the actual distortion between the original and the tampered signal is higher than the maximum tolerated distortion determined by the original CP, decoding might fail.
-
(i)
-
(4)
Distortion Estimation
If Wyner-Ziv decoding succeeds, an estimate of the distortion in terms of a perceptual signal-to-noise ratio is computed using the projections of the subsampled energy spectrum of the tampering. Let
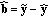 be the projections of the subsampled energy spectrum of the tampering; we define the perceptual signal-to-noise ratio (
be the projections of the subsampled energy spectrum of the tampering; we define the perceptual signal-to-noise ratio ( ) of the received audio stream as
) of the received audio stream as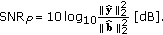 (13)
(13)This definition needs some further interpretation. In fact, we compute the
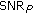 from the projections in place of the whole time-frequency perceptual map of both the signal and the tampering. This is justified by the energy conservation principle stated in (11) and by the fact that, at the CU side, no information about the authentic audio content is available; hence, this is an approximation of the actual
from the projections in place of the whole time-frequency perceptual map of both the signal and the tampering. This is justified by the energy conservation principle stated in (11) and by the fact that, at the CU side, no information about the authentic audio content is available; hence, this is an approximation of the actual  , which uses the quantized projections obtained by decoding the hash signature, in the reasonable hypothesis that
, which uses the quantized projections obtained by decoding the hash signature, in the reasonable hypothesis that 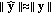 and
and 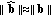 .
. -
(5)
Tampering Estimation
If the tampering can be represented by a sparse set of coefficients in some basis  , it can be reconstructed starting from the random projections
, it can be reconstructed starting from the random projections  by solving the following optimization problem, as anticipated in Section 2.1:
by solving the following optimization problem, as anticipated in Section 2.1:

For a given orthonormal basis  , the expansion of the tampering in that basis, that is,
, the expansion of the tampering in that basis, that is,  , might not be sparse enough with respect to the number of available random projections
, might not be sparse enough with respect to the number of available random projections  and the optimization algorithm might not converge to a feasible solution. In such cases, it is not possible to perform tampering identification, and a different orthonormal basis
and the optimization algorithm might not converge to a feasible solution. In such cases, it is not possible to perform tampering identification, and a different orthonormal basis  is tested. If the optimization algorithm does not converge for any of the tested bases, the tampering is declared to be nonsparse. This is the case, for example, of quantization noise introduced by audio compression. If the reconstruction succeeds for more than one basis, we choose the one in which the tampering is the sparsest. While, in principle, this just means that we should take the basis that returns the smallest
is tested. If the optimization algorithm does not converge for any of the tested bases, the tampering is declared to be nonsparse. This is the case, for example, of quantization noise introduced by audio compression. If the reconstruction succeeds for more than one basis, we choose the one in which the tampering is the sparsest. While, in principle, this just means that we should take the basis that returns the smallest  metrics, we have in practice to cope with reconstruction noise, which in fact prevents the recovered tampering to be exactly sparse. A simple solution is to select the basis that gives the smallest
metrics, we have in practice to cope with reconstruction noise, which in fact prevents the recovered tampering to be exactly sparse. A simple solution is to select the basis that gives the smallest  norm; however, this approach has the drawback of being too sensitive toward high values of the coefficients (e.g., due to different dynamic ranges in the transform domains). As experimentally shown in Section 7.2, this bias has the side-effect that selecting the minimum
norm; however, this approach has the drawback of being too sensitive toward high values of the coefficients (e.g., due to different dynamic ranges in the transform domains). As experimentally shown in Section 7.2, this bias has the side-effect that selecting the minimum  norm reconstruction does not ensure that one is performing the best possible tampering estimation. A more effective heuristic is to use some
norm reconstruction does not ensure that one is performing the best possible tampering estimation. A more effective heuristic is to use some  metrics, with
metrics, with  , or similar norms, as the ones devised in [32]. In our experiments, we have computed the norm of the coefficients
, or similar norms, as the ones devised in [32]. In our experiments, we have computed the norm of the coefficients  as
as

where  has been set so that
has been set so that  .
.
5. Choice of the Hash Parameters
In the hash construction procedure, there are two parameters that influence the quality of tampering estimation. The number of random projections  used to build the hash, and the number of bitplanes
used to build the hash, and the number of bitplanes  which determines the distortion due to quantization on the reconstructed measurements at the user side. In this section we analyze the tradeoff between the rate needed to encode the hash, which also depends on the maximum allowed tampering level as explained in Section 6, and the accuracy of the tampering estimation; a larger number of bitplanes
which determines the distortion due to quantization on the reconstructed measurements at the user side. In this section we analyze the tradeoff between the rate needed to encode the hash, which also depends on the maximum allowed tampering level as explained in Section 6, and the accuracy of the tampering estimation; a larger number of bitplanes  and of measurements
and of measurements  correspond to a higher quality of tampering estimation, and at the same time to a higher rate spent for the hash. In order to find an optimal tradeoff between
correspond to a higher quality of tampering estimation, and at the same time to a higher rate spent for the hash. In order to find an optimal tradeoff between  and
and  , we conducted Monte carlo simulations on a generic sparse signal
, we conducted Monte carlo simulations on a generic sparse signal  , with two different sparsity levels
, with two different sparsity levels  . We evaluate the goodness of the tampering estimation by calculating the reconstruction normalized MSE (
. We evaluate the goodness of the tampering estimation by calculating the reconstruction normalized MSE ( ) between the original
) between the original  -sparse signal
-sparse signal  and its approximation
and its approximation  obtained by solving problem (4)
obtained by solving problem (4)

The noise  in (4) in this case corresponds to quantization noise, which is uniformly distributed between
in (4) in this case corresponds to quantization noise, which is uniformly distributed between  and
and  , where
, where  is the quantization step size. We measure the impact of quantization noise by measuring the signal-to-quantization noise ratio
is the quantization step size. We measure the impact of quantization noise by measuring the signal-to-quantization noise ratio

where  is the quantized version of the random projections
is the quantized version of the random projections  . As for the reconstruction basis,
. As for the reconstruction basis,  , we just assign
, we just assign  in (4), that is, we assume that the signal is sparse as is, or equivalently that some oracle has told us the optimal sparsifying basis in advance. Figure 3 shows the
in (4), that is, we assume that the signal is sparse as is, or equivalently that some oracle has told us the optimal sparsifying basis in advance. Figure 3 shows the  contour set for two levels of sparsity (
contour set for two levels of sparsity ( and
and  ) as a function of the number of projections
) as a function of the number of projections  and of the quantization distortion of the measurements (
and of the quantization distortion of the measurements ( ). We observe a graceful improvement of the performance by increasing either
). We observe a graceful improvement of the performance by increasing either  or
or  . For the same values of the parameters, the normalized MSE of the reconstructed signal is lower for sparser signals (
. For the same values of the parameters, the normalized MSE of the reconstructed signal is lower for sparser signals ( ). This is justified by the CS result on the number of projections which requires
). This is justified by the CS result on the number of projections which requires  (see Section2.1). Thus the contour set for
(see Section2.1). Thus the contour set for  appears as it was "shifted" to the right with respect to the case
appears as it was "shifted" to the right with respect to the case  in Figure 3. As for the quantization of the projections, provided that the number of measurements is compatible with the sparsity level as explained before, we can observe that the value of
in Figure 3. As for the quantization of the projections, provided that the number of measurements is compatible with the sparsity level as explained before, we can observe that the value of  decreases as
decreases as  becomes larger. In a practical scenario, the quantization step size
becomes larger. In a practical scenario, the quantization step size  should be chosen in such a way to attain
should be chosen in such a way to attain  dB, in order to be robust with the choice of
dB, in order to be robust with the choice of  , which depends on the actual sparsity of the tampering and on the constant
, which depends on the actual sparsity of the tampering and on the constant  and is therefore unknown at the CP side. In our experiments in the rest of the paper, we have set
and is therefore unknown at the CP side. In our experiments in the rest of the paper, we have set  .
.
6. Rate Allocation
In Section 3 we have shown that the correlation model between the original and the tampered random projections can be written as

Hereafter, we assume that  and
and  are statistically independent. This is reasonable if the tampering is considered independent from the original audio content.
are statistically independent. This is reasonable if the tampering is considered independent from the original audio content.
Let  denote the bitplane index and
denote the bitplane index and  the bitrate (in bits/symbol) needed to decode the
the bitrate (in bits/symbol) needed to decode the  th bitplane. As mentioned in Section 3, the probability density function of
th bitplane. As mentioned in Section 3, the probability density function of  and
and  can be well approximated to be zero mean Gaussian, respectively, with variance
can be well approximated to be zero mean Gaussian, respectively, with variance  and
and  . The rate estimation algorithm receives in input the source variance
. The rate estimation algorithm receives in input the source variance  , the correlation noise variance
, the correlation noise variance  , the quantization step size
, the quantization step size  , and the number of bitplanes to be encoded
, and the number of bitplanes to be encoded  and returns the average number of bits needed to decode each bitplane
and returns the average number of bits needed to decode each bitplane  . The value of
. The value of  can be immediately estimated from the random projections at the time of hash generation. The value of
can be immediately estimated from the random projections at the time of hash generation. The value of  is set to be equal to the maximum MSE distortion between the original and the tampered signal, for which tampering identification can be attempted.
is set to be equal to the maximum MSE distortion between the original and the tampered signal, for which tampering identification can be attempted.
The rate allocated to each bitplane is given by

where  denotes the
denotes the  th bitplane of
th bitplane of  . In fact LDPC decoding of bitplane
. In fact LDPC decoding of bitplane  exploits the knowledge of the real-valued side information
exploits the knowledge of the real-valued side information  as well as previously decoded bitplanes
as well as previously decoded bitplanes  . Since we use nonideal channel codes with a finite sequence length
. Since we use nonideal channel codes with a finite sequence length  to perform source coding a rate overhead of approximately
to perform source coding a rate overhead of approximately  [bit/sample
[bit/sample is added. The integral needed to compute the value of the conditional entropy in (19) is factored out in detail in our previous work [33].
is added. The integral needed to compute the value of the conditional entropy in (19) is factored out in detail in our previous work [33].
7. Experimental Results
We have carried out some experiments on 32 seconds of speech audio data, sampled at 44100 Hz and 16 bits per sample. The test audio consists of a piece of a newspaper article read by a speaker; the recording is clean but for some noise added at a few time instants, including the high frequency noise of a shaken key ring, the wide-band noise of some crumpling paper, and some impulsive noise in the form of coughs of the speaker. We have set the size of the audio frame to  samples (0.25 seconds), and the number of Mel frequency bands to
samples (0.25 seconds), and the number of Mel frequency bands to  , obtaining a total of 128 audio frames corresponding to
, obtaining a total of 128 audio frames corresponding to  log-energy coefficients. We have then assembled a testbed considering 3 kinds of tampering.
log-energy coefficients. We have then assembled a testbed considering 3 kinds of tampering.
Time Localized Tampering (T)
We have replaced some words in the speech at different positions, for a total tampering length of 3.75 seconds (about 11.7% of the total length of the audio sequence).
Frequency Localized Tampering (F)
A low-pass phone-band filter (cut-off frequency at 3400 Hz and stop frequency at 4000 Hz) is applied to the entire original audio stream.
Time-Frequency Localized Tampering (TF)
A cough at the beginning of the stream and the noise of the key ring in the middle are canceled out using the standard noise removal tool of the "Audacity" free audio editing software [34]. The noise removal tool implemented in this application is an adaptive filter, whose frequency response depends on the local frequency characteristics of the noise. In this case, the total time length of the attack is 4.36 seconds.
The reconstruction of the tampering has been attempted in 3 different bases, besides the log-energy domain: 1D DCT (discrete cosine transform across frequency bands of the same frame; this corresponds to extracting Mel frequency cepstral coefficients), 2D DCT (across time and frequency), and 2D Haar wavelet. Table 1 summarizes the perceptual SNRs and the sparsity of the three tampering examples, in the domain where its values is the lowest. It also reports the number of computed projections  in terms of the ratio
in terms of the ratio  . Note that this ratio is always less than one (i.e.,
. Note that this ratio is always less than one (i.e.,  ), thus the adopted setting is coherent with the compressive sensing framework explained in Section 2.1. In the following, we evaluate two aspects of the system, namely: (1) the rate spent for Wyner-Ziv encoding the hash with respect to the rate that would have been spent for encoding and transmitting the projections without DSC; (2) the relation between the
), thus the adopted setting is coherent with the compressive sensing framework explained in Section 2.1. In the following, we evaluate two aspects of the system, namely: (1) the rate spent for Wyner-Ziv encoding the hash with respect to the rate that would have been spent for encoding and transmitting the projections without DSC; (2) the relation between the  and the inverse tangent norms of the quality of the reconstructed tampering in different domains.
and the inverse tangent norms of the quality of the reconstructed tampering in different domains.
 in the most "sparsifying" basis (in parentheses) and
in the most "sparsifying" basis (in parentheses) and  ratio for the three considered tampering example.
ratio for the three considered tampering example.7.1. Rate-Distortion Performance of the Hash Signature
As described in Section 4, we use distributed source coding for reducing the payload due to the hash. In this section, we want to quantify the bit-saving obtained with Wyner-Ziv coding of the hash. In order to do so, we have compared the rate distortion function of Wyner-Ziv (WZ) coding and of hash direct quantization and transmission, that is, without using DSC (NO-WZ). Figure 4 depicts these two situations for the cases of the frequency and time domain tampering. In both the two graphs, the value of quantization MSE has been normalized by the energy of the measurements  , in order to make the result comparable with other possible manipulations
, in order to make the result comparable with other possible manipulations

The bold-dotted lines represents the theoretical WZ rate-distortion curve of the measurements stated in (7). The bold solid and dashed lines represent instead the actual rate-distortion behavior obtained by using a practical WZ codec, either using the feedback channel or directly estimating at the encoder side the rate as explained in Section 6. For comparison, we have also plotted the rate-distortion functions of an ideal NO-WZ uniform quantizer (Shannon's bound), drawn as a thin-dotted line, and the rate-distortion curve of an entropy-constrained scalar quantization (ECSQ), which is a well studied and effective practical quantization scheme (thin-solid line).
We can make two main comments on the curves in the two graphs of Figure 4. The first difference between the frequency and the time tampering is that all the rate-distortion functions in the frequency attack are shifted upwards to higher rates, and have a steeper descending slope as the distortion increases. This is due to the fact that the frequency manipulation has a higher sparsity coefficient  , that is, more measurements are needed for signal reconstruction. Although in the real application no guess about the sparsity of the tampering can be made at the CP side, here we have fixed a different sparsity for the two kinds of attacks, in order to visually prove the effect of the number of measures on the hash length. Thus, even if the rate per measurement is the same in both the cases (it only depends on the signal energy, as expressed in (5) and (7)), the rate in bits per second has slopes and offsets proportional to the number of measurements
, that is, more measurements are needed for signal reconstruction. Although in the real application no guess about the sparsity of the tampering can be made at the CP side, here we have fixed a different sparsity for the two kinds of attacks, in order to visually prove the effect of the number of measures on the hash length. Thus, even if the rate per measurement is the same in both the cases (it only depends on the signal energy, as expressed in (5) and (7)), the rate in bits per second has slopes and offsets proportional to the number of measurements  . Clearly, if we did not use compressive sensing to reduce the dimensionality of the data (i.e.,
. Clearly, if we did not use compressive sensing to reduce the dimensionality of the data (i.e.,  in our setting), the rate required for the hash would have been equivalent to using random projections with
in our setting), the rate required for the hash would have been equivalent to using random projections with  ; therefore, the rate saving due to compressive sensing is approximately equal to the ratio
; therefore, the rate saving due to compressive sensing is approximately equal to the ratio  . The second interesting remark that emerges from Figure 4 is the different gap between the family of WZ rates (ideal, with feedback and without feedback) and the NO-WZ curves. As (8) suggests, the coding gain from NO-WZ to WZ strongly depends on the energy of the tampering, that is, to
. The second interesting remark that emerges from Figure 4 is the different gap between the family of WZ rates (ideal, with feedback and without feedback) and the NO-WZ curves. As (8) suggests, the coding gain from NO-WZ to WZ strongly depends on the energy of the tampering, that is, to  (see Table 1). In the case of time attack, we have
(see Table 1). In the case of time attack, we have  dB, while
dB, while  dB, thus according to (8) the bit saving achieved with WZ is smaller in the case of the frequency attack. As can be inferred from the graphs, this gain ranges from 20% to 70%.
dB, thus according to (8) the bit saving achieved with WZ is smaller in the case of the frequency attack. As can be inferred from the graphs, this gain ranges from 20% to 70%.
7.2. Choice of the Best Tampering Reconstruction
In practice, the tampering may be sparse or compressible in more than one basis: this may be the case, for instance, of piece-wise polynomials signals which are generally sparse in several wavelet expansions. When this situation occurs, multiple tampering reconstructions are possible, and at the CU side there is an ambiguity about what is the best tampering estimation. As described in Section 4.2, we are ultimately interested in finding the sparsest tampering representation. This requires in practice to evaluate the sparsity of the tampering in each basis expansion; we use for this purpose the inverse-tangent norm defined in (15). To validate the choice of this norm, we compare the optimal basis expansion predicted from the  norm and the inverse tangent norm with the actual best basis in terms of
norm and the inverse tangent norm with the actual best basis in terms of  reconstruction quality.
reconstruction quality.
We evaluate the goodness of the tampering estimation by calculating the reconstruction normalized MSE between the log-energy spectrum of the original tampering and the log-energy spectrum of the estimated one

Reconstruction NMSE values obtained with a fixed bit-rate for the hash are shown in Tables 2 (for 200 bps) and 3 (for 400 bps). The bit rate depends on the number of measurements  (given in Table 1) and on the number of bitplanes per measurement
(given in Table 1) and on the number of bitplanes per measurement  . For a resulting rate of 200 bps, the number of bitplanes for the three kinds of attack (T, F, TF) is, respectively, 7, 5, and 6. When the rate is 400 bps, we have
. For a resulting rate of 200 bps, the number of bitplanes for the three kinds of attack (T, F, TF) is, respectively, 7, 5, and 6. When the rate is 400 bps, we have  for the time attack,
for the time attack,  for the frequency attack, and
for the frequency attack, and  for the time-frequency tampering. From the tables it is clear that, by looking for a sparse tampering in other bases besides the canonical one (log-energy), better results can be achieved using the same hash length, as highlighted by the bold numbers in the tables. In particular, it can be observed that the wide-band, time-localized tampering is better reconstructed using the 1D-DCT basis, which is able to capture tampering correlations only along the frequency axis, avoiding tampering discontinuities over time. The frequency-localized tampering is better reconstructed using the 2D-DCT basis, due to its time extension and wide-band characterization which exhibits only a single discontinuity along the frequency axis. Finally, Haar wavelet is a good compromise to detect time-frequency localized tampering because it is able to deal with discontinuities along both time and frequency axes.
for the time-frequency tampering. From the tables it is clear that, by looking for a sparse tampering in other bases besides the canonical one (log-energy), better results can be achieved using the same hash length, as highlighted by the bold numbers in the tables. In particular, it can be observed that the wide-band, time-localized tampering is better reconstructed using the 1D-DCT basis, which is able to capture tampering correlations only along the frequency axis, avoiding tampering discontinuities over time. The frequency-localized tampering is better reconstructed using the 2D-DCT basis, due to its time extension and wide-band characterization which exhibits only a single discontinuity along the frequency axis. Finally, Haar wavelet is a good compromise to detect time-frequency localized tampering because it is able to deal with discontinuities along both time and frequency axes.
 for tampering reconstruction with a hash at a bit rate of 200 bps.
for tampering reconstruction with a hash at a bit rate of 200 bps. for tampering reconstruction with a hash at a bit rate of 400 bps.
for tampering reconstruction with a hash at a bit rate of 400 bps.Tables 4 and 5 show the  norms of the reconstructed tampering coefficients in the four analyzed bases. Note that at a rate equal to 200 bps, the
norms of the reconstructed tampering coefficients in the four analyzed bases. Note that at a rate equal to 200 bps, the  norm suggests, for the time-frequency (TF) tampering, that the best reconstruction is with the 1D-DCT coefficients. However, Table 2 indicates that the best reconstruction is actually in the Haar wavelet domain. This is due to the noise introduced by compressive sensing recovery at low rates, which makes the use of the
norm suggests, for the time-frequency (TF) tampering, that the best reconstruction is with the 1D-DCT coefficients. However, Table 2 indicates that the best reconstruction is actually in the Haar wavelet domain. This is due to the noise introduced by compressive sensing recovery at low rates, which makes the use of the  norm as an estimator of the sparsity more error-prone. This effect is partially alleviated using the inverse tangent norm, as shown in Tables 6 and 7.
norm as an estimator of the sparsity more error-prone. This effect is partially alleviated using the inverse tangent norm, as shown in Tables 6 and 7.
 -norm of the tampering using a fixed bit-rate for the hash signature of 200 bps.
-norm of the tampering using a fixed bit-rate for the hash signature of 200 bps. -norm of the tampering using a fixed bit-rate for the hash signature of 400 bps.
-norm of the tampering using a fixed bit-rate for the hash signature of 400 bps.To have a visual insight of the effect of different bases in the tampering reconstruction, we have drawn in Figure 5 the log-energy spectrum of the original audio signal and of the frequency-localized (F) tampering, followed by the log-energy spectrum of the tampering reconstructed in two different domains using a hash rate of 200 bps. It apparent from the figure that the quality of the estimated tampering reconstructed using 2D-DCT considerably overcomes the one obtained in the log-energy domain.
8. Conclusions
We presented a hash-based tampering identification system for detecting and identifying illegitimate manipulations in audio files. The algorithm works with sparse modifications, leveraging the recent compressive sensing results for reconstructing the tampering from a set of random nonadaptive measurements. Perhaps the most distinctive feature of the proposed system is its ability to reconstruct a tampering that is sparse in some orthonormal basis or frame, without knowing at the CP side the actual content alteration. In practice, such an approach is feasible only if the bit length of the hash is not too large; we have found that encoding the hash signature through a distributed source coding paradigm enables a consistent reduction of the transmitted bits, especially when the strength of the tampering is small compared to the original signal energy. The hash size may be further decreased in the future by considering weighted  minimization [32] to reduce the number of measurements required by the algorithm.
minimization [32] to reduce the number of measurements required by the algorithm.
References
Steinebach M, Dittmann J: Watermarking-based digital audio data authentication. EURASIP Journal on Applied Signal Processing 2003,2003(10):1001-1015. 10.1155/S1110865703304081
Fridrich J: Image watermarking for tamper detection. Proceedings of IEEE International Conference on Image Processing (ICIP '98), October 1998, Chicago, Ill, USA 2: 404-408.
Eggers JJ, Girod B: Blind watermarking applied to image authentication. Proceedings of IEEE International Conference on Acoustics, Speech, and Signal Processing (ICASSP '01), May 2001, Salt Lake, Utah, USA 3: 1977-1980.
Kundur D, Hatzinakos D: Digital watermarking for telltale tamper proofing and authentication. Proceedings of the IEEE 1999,87(7):1167-1180. 10.1109/5.771070
Tu R, Zhao J: A novel semi-fragile audio watermarking scheme. Proceedings of the 2nd IEEE Internatioal Workshop on Haptic, Audio and Visual Environments and Their Applications (HAVE '03), September 2003, Ottawa, Canada 89-94.
Wong PW: A public key watermark for image verification and authentication. Proceedings of IEEE International Conference on Image Processing (ICIP '98), October 1998, Chicago, Ill, USA 1: 455-459.
Celik MU, Sharma G, Saber E, Tekalp AM: Hierarchical watermarking for secure image authentication with localization. IEEE Transactions on Image Processing 2002,11(6):585-595. 10.1109/TIP.2002.1014990
Lu C-S, Huang S-K, Sze C-J, Liao H-YM: Cocktail watermarking for digital image protection. IEEE Transactions on Multimedia 2000,2(4):209-224. 10.1109/6046.890056
Lu C-S, Liao H-YM, Chen L-H: Multipurpose audio watermarking. Proceedings of the 15th International Conference on Pattern Recognition (ICPR '00), September 2000, Barcelona, Spain 3: 282-285.
Mıhçak MK, Venkatesan R: A perceptual audio hashing algorithm: a tool for robust audio identification and information hiding. Proceedings of the 4th International Workshop on Information Hiding (IH '01), April 2001, Pittsburgh, Pa, USA 2137: 51-65.
Haitsma J, Kalker T: A highly robust audio fingerprinting system with an efficient search strategy. Journal of New Music Research 2003,32(2):211-221. 10.1076/jnmr.32.2.211.16746
Cano P, Batlle E, Kalker T, Haitsma J: A review of algorithms for audio fingerprinting. Proceedings of IEEE Workshop on Multimedia Signal Processing (MMSP '02), December 2002, St. Thomas, Virgin Islands, USA 169-173.
Roy S, Sun Q: Robust hash for detecting and localizing image tampering. Proceedings of the 14th IEEE International Conference on Image Processing (ICIP '07), October 2007, San Antonio, Tex, USA 6: 117-120.
Lin Y-C, Varodayan D, Girod B: Image authentication based on distributed source coding. Proceedings of IEEE International Conference on Image Processing (ICIP '07), September-October 2007, San Antonio, Tex, USA 3: 5-8.
Lin Y-C, Varodayan D, Girod B: Spatial models for localization of image tampering using distributed source codes. Proceedings of the International Picture Coding Symposium (PCS '07), November 2007, Lisbon, Portugal
Chono K, Lin Y-C, Varodayan D, Miyamoto Y, Girod B: Reduced-reference image quality estimation using distributed source coding. Proceedings of IEEE International Conference on Multimedia and Expo (ICME '08), June 2008, Hannover, Germany
Varodayan D, Lin Y-C, Girod B: Audio authentication based on distributed source coding. Proceedings of IEEE International Conference on Acoustics, Speech, and Signal Processing (ICASSP '08), March-April 2008, Las Vegas, Nev, USA 225-228.
Tagliasacchi M, Valenzise G, Tubaro S: Localization of sparse image tampering via random projections. Proceedings of the 15th IEEE International Conference on Image Processing (ICIP '08), October 2008, San Diego, Calif, USA 2092-2095.
Candès EJ: Compressive sampling. Proceedings of the International Congress of Mathematicians (ICM '06), August 2006, Madrid, Spain
Baraniuk RG: Compressive sensing. IEEE Signal Processing Magazine 2007,24(4):118-121.
Candès EJ, Wakin MB: An introduction to compressive sampling: a sensing/sampling paradigm that goes against the common knowledge in data acquisition. IEEE Signal Processing Magazine 2008,25(2):21-30.
Slepian D, Wolf JK: Noiseless coding of correlated information sources. IEEE Transactions on Information Theory 1973,19(4):471-480. 10.1109/TIT.1973.1055037
Wyner A, Ziv J: The rate-distortion function for source coding with side information at the decoder. IEEE Transactions on Information Theory 1976,22(1):1-10. 10.1109/TIT.1976.1055508
Girod B, Aaron AM, Rane S, Rebollo-Monedero D: Distributed video coding. Proceedings of the IEEE 2005,93(1):71-83.
Goyal VK, Fletcher AK, Rangan S: Compressive sampling and lossy compression: do random measurements provide an efficient method of representing sparse signals? IEEE Signal Processing Magazine 2008,25(2):48-56.
Boyd S, Vandenberghe L: Convex Optimization. Cambridge University Press, Cambridge, UK; 2004.
van den Berg E, Friedlander MP: In pursuit of a root. Department of Computer Science, University of British Columbia, Vancouver, Canada; June 2007.http://www.optimization-online.org/DB_FILE/2007/06/1708.pdf preprint ,
Varodayan D, Aaron A, Girod B: Rate-adaptive codes for distributed source coding. Signal Processing 2006,86(11):3123-3130. 10.1016/j.sigpro.2006.03.012
Artigas X, Ascenso J, Dalai M, Klomp S, Kubasov D, Ouaret M: The DISCOVER codec: architecture, techniques and evaluation. Proceedings of the International Picture Coding Symposium (PCS '07), November 2007, Lisbon, Portugal 6: 14496-14410.
Cover TM, Thomas JA: Elements of Information Theory. John Wiley & Sons, New York, NY, USA; 1991.
Rabiner L, Juang BH: Fundamentals of Speech Recognition. Prentice-Hall, Upper Saddle River, NJ, USA; 1993.
Candès EJ, Wakin MB, Boyd SP: Enhancing sparsity by reweighted
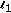 minimization. Journal of Fourier Analysis and Applications 2008,14(5-6):877-905. 10.1007/s00041-008-9045-x
minimization. Journal of Fourier Analysis and Applications 2008,14(5-6):877-905. 10.1007/s00041-008-9045-xBernardini R, Naccari M, Rinaldo R, Tagliasacchi M, Tubaro S, Zontone P: Rate allocation for robust video streaming based on distributed video coding. Signal Processing: Image Communication 2008,23(5):391-403. 10.1016/j.image.2008.04.004
Audacity http://audacity.sourceforge.net
Acknowledgment
This work has been partially sponsored by the EU under Visnet II Network of Excellence.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Valenzise, G., Prandi, G., Tagliasacchi, M. et al. Identification of Sparse Audio Tampering Using Distributed Source Coding and Compressive Sensing Techniques. J Image Video Proc 2009, 158982 (2009). https://doi.org/10.1155/2009/158982
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1155/2009/158982


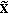 received by the CU is computed using the same algorithm described above for the CP side. At this step, the vector
received by the CU is computed using the same algorithm described above for the CP side. At this step, the vector 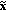 is produced.
is produced.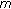 linear random measurements
linear random measurements 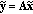 are computed using a pseudorandom matrix
are computed using a pseudorandom matrix 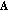 whose entries are drawn from a Gaussian distribution with the same seed
whose entries are drawn from a Gaussian distribution with the same seed 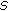 as the encoder.
as the encoder.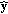 is obtained using the hash syndrome bits and
is obtained using the hash syndrome bits and 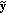 as side information. LDPC decoding is performed starting from the most significant bitplane.
as side information. LDPC decoding is performed starting from the most significant bitplane.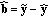 be the projections of the subsampled energy spectrum of the tampering; we define the perceptual signal-to-noise ratio (
be the projections of the subsampled energy spectrum of the tampering; we define the perceptual signal-to-noise ratio ( ) of the received audio stream as
) of the received audio stream as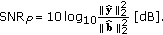
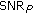 from the projections in place of the whole time-frequency perceptual map of both the signal and the tampering. This is justified by the energy conservation principle stated in (11) and by the fact that, at the CU side, no information about the authentic audio content is available; hence, this is an approximation of the actual
from the projections in place of the whole time-frequency perceptual map of both the signal and the tampering. This is justified by the energy conservation principle stated in (11) and by the fact that, at the CU side, no information about the authentic audio content is available; hence, this is an approximation of the actual  , which uses the quantized projections obtained by decoding the hash signature, in the reasonable hypothesis that
, which uses the quantized projections obtained by decoding the hash signature, in the reasonable hypothesis that 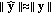 and
and 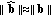 .
.
 and the measures signal-to-quantization noise ratio
and the measures signal-to-quantization noise ratio  , expressed in dB.
, expressed in dB.


 set to 0.15 Frequency sparse tampering, with sparsity factor
set to 0.15 Frequency sparse tampering, with sparsity factor 

 minimization. Journal of Fourier Analysis and Applications 2008,14(5-6):877-905. 10.1007/s00041-008-9045-x
minimization. Journal of Fourier Analysis and Applications 2008,14(5-6):877-905. 10.1007/s00041-008-9045-x