- Research Article
- Open access
- Published:
Image Segmentation Method Using Thresholds Automatically Determined from Picture Contents
EURASIP Journal on Image and Video Processing volume 2009, Article number: 140492 (2009)
Abstract
Image segmentation has become an indispensable task in many image and video applications. This work develops an image segmentation method based on the modified edge-following scheme where different thresholds are automatically determined according to areas with varied contents in a picture, thus yielding suitable segmentation results in different areas. First, the iterative threshold selection technique is modified to calculate the initial-point threshold of the whole image or a particular block. Second, the quad-tree decomposition that starts from the whole image employs gray-level gradient characteristics of the currently-processed block to decide further decomposition or not. After the quad-tree decomposition, the initial-point threshold in each decomposed block is adopted to determine initial points. Additionally, the contour threshold is determined based on the histogram of gradients in each decomposed block. Particularly, contour thresholds could eliminate inappropriate contours to increase the accuracy of the search and minimize the required searching time. Finally, the edge-following method is modified and then conducted based on initial points and contour thresholds to find contours precisely and rapidly. By using the Berkeley segmentation data set with realistic images, the proposed method is demonstrated to take the least computational time for achieving fairly good segmentation performance in various image types.
1. Introduction
Image segmentation is an important signal processing tool that is widely employed in many applications including object detection [1], object-based coding [2–4], object tracking [5], image retrieval [6], and clinical organ or tissue identification [7]. To accomplish segmentations in these applications, the methods can be generally classified as region-based and edge-based techniques. The region-based segmentation techniques such as semisupervised statistical region refinement [8], watershed [9], region growing [10], and Markov-random-field parameter estimation [11] focus on grouping pixels to become regions which have uniform properties like grayscale, texture, and so forth. The edge-based segmentation techniques such as Canny edge detector [12], active contour [13], and edge following [14–16] emphasize on detecting significant gray-level changes near object boundaries. Regarding to the above-mentioned methods, the segmenting mechanisms associated with users can be further categorized as either supervised segmentation or unsupervised segmentation.
The advantage of the region-based segmentation is that the segmented results can have coherent regions, linking edges, no gaps from missing edge pixels, and so on. However, its drawback is that decisions about region memberships are often more difficult than those about edge detections. In the literature, the Semisupervised Statistical Region Refinement (SSRR) method developed by Nock and Nielsen is to segment an image with user-defined biases which indicate regions with distinctive subparts [8]. SSRR is fairly accurate because the supervised segmentation is not easily influenced by noise, but is highly time-consuming. The unsupervised DISCovering Objects in Video (DISCOV) technique developed by Liu and Chen could discover the major object of interest by an appearance model and a motion model [1]. The watershed method that is applicable to nonspecific image type is also unsupervised [9, 17]. The implementation manners of the watershed method can be classified into rain falling and water immersion [18]. Some recent watershed methods use the prior information-based difference function instead of the more-frequently-used gradient function to improve the segmented results [19] and employ the marker images as probes to explore a gradient space of an unknown image and thus to determine the best-matched object [20]. The advantage of the watershed method is that it can segment multiple objects in a single threshold setting. The disadvantage of the watershed method is that the different types of images need different thresholds. If the thresholds are not set correctly, then the objects are under-segmented or over-segmented. Additionally, slight changes in the threshold can significantly alter the segmentation results. In [21, 22], the systematic approach was demonstrated to analyze nature images by using a Binary Partition Tree (BPT) for the purposes of archiving and segmentation. BPTs are generated based on a region merging process which is uniquely specified by a region model, a merging order, and a merging criterion. By studying the evolution of region statistics, this unsupervised method highlights nodes which represent the boundary between salient details and provide a set of tree levels from which segmentations can be derived.
The edge-based segmentation can simplify the analysis by drastically minimizing the amount of pixels from an image to be processed, while still preserving adequate object structures. The drawback of the edge-based segmentation is that the noise may result in an erroneous edge. In the literature, the Canny edge detector employed the hysteresis threshold that adapts to the amount of noise in an image, to eliminate streaking of edge contours where the detector is optimized by three criteria of detection, localization, and single response [12]. The standard deviation of the Gaussian function associated with the detector is adequately determined by users. The Live Wire On the Fly (LWOF) method proposed by Falcao et al. helps the user to obtain an optimized route between two initial points [23]. The user can follow the object contour and select many adequate initial points to accomplish that an enclosed contour is found. The benefit of LWOF is that it is adaptive to any type of images. Even with very complex backgrounds, LWOF can enlist human assistance in determining the contour. However, LWOF is limited in that if a picture has multiple objects, each object needs to be segmented individually and the supervised operation significantly increases the operating time. The other frequently adopted edge-based segmentation is the snake method first presented by Kass et al. [24]. In this method, after an initial contour is established, partial local energy minima are calculated to derive the correct contour. The flaw of the snake method is that it must choose an initial contour manually. The operating time rises with the number of objects segmented. Moreover, if the object is located within another object, then the initial contours are also difficult to select. On the other hand, Yu proposed a supervised multiscale segmentation method in which every pixel becomes a node, and the likelihood of two nodes belonging together is interpreted by a weight attached to the edge linking these two pixel nodes [25]. Such approach allows that image segmentation becomes a weighted graph partitioning problem that is solved by average cuts of normalized affinity. The above-mentioned supervised segmentation methods are suitable for conducting detailed processing to objects of segmentation under user's assistance. In the unsupervised snake method also named as the active contour scheme, the geodesic active contours and level sets were proposed to detect and track multiple moving objects in video sequences [26, 27]. However, the active contour scheme is generally applied when segmenting stand-alone objects within an image. For instance, an object located within the complicated background may not be easily segmented. Additionally, contours that are close together cannot be precisely segmented. Relevant study, the Extended-Gradient Vector Flow (E-GVF) snake method proposed by Chuang and Lie has improved upon the conventional snake method [28]. The E-GVF snake method can automatically derive a set of seeds from the local gradient information surrounding each point, and thus can achieve unsupervised segmentation without manually specifying the initial contour. The noncontrast-based edge descriptor and mathematical morphology method were developed by Kim and Park and Gao et al., respectively, for unsupervised segmentation to assist object-based video coding [29, 30].
The conventional edge-following method is another edge-based segmentation approach that can be applied to nonspecific image type [14, 31]. The fundamental step of the edge-following method attempts to find the initial points of an object. With these initial points, the method then follows on contours of an object until it finds all points matching the criteria, or it hits the boundary of a picture. The advantage of the conventional edge-following method is its simplicity, since it only has to compute the gradients of the eight points surrounding a contour point to obtain the next contour point. The search time for the next contour point is significantly reduced because many points within an object are never used. However, the limitation of the conventional edge-following method is that it is easily influenced by noise, causing it to fall into the wrong edge. This wrong edge can form a wrong route to result in an invalid segmented area. Moreover, the fact that initial points are manually selected by users may affect accuracy of segmentation results due to inconsistence in different times for selection. To improve on these drawbacks, the initial-point threshold calculated from the histogram of gradients in an entire image is adopted to locate positions of initial points automatically [15]. Additionally, the contour thresholds are employed to eliminate inappropriate contours to increase the accuracy of the search and to minimize the required searching time. However, this method is limited in that the initial-point threshold and contour threshold remain unchanged throughout the whole image. Hence, optimized segmentations cannot always be attained in areas with complicated and smooth gradients. If the same initial-point threshold is employed throughout an image with areas having different characteristics, for example, a half of the image is smooth, and the other half has major changes in gradients, then the adequately segmented results can clearly only be obtained from one side of the image, while the objects from the other side are not accurately segmented.
This work proposes a robust segmentation method that is suitable for nonspecific image type. Based on the hierarchical segmentation under a quad-tree decomposition [32, 33], an image is adequately decomposed into many blocks and subblocks according to the image contents. The initial-point threshold in each block is determined by the modified iterative threshold selection technique and the initial-point threshold of its parent block. Additionally, the contour threshold is calculated based on the histogram of gradients in each block. Using these two thresholds, the modified edge-following scheme is developed to automatically and rapidly attain fairly good segmentation results. Segmentations on various types of images are performed during simulations to obtain the accuracy of segmentations using methods such as the proposed, watershed, active contour, and others. To do fair comparison, the data set and benchmarks from the Computer Vision Group, University of California at Berkeley were used [34]. Simulation results demonstrate that the proposed method is superior to the conventional methods to some extent. Owing to avoiding human interferences and reducing operating time, the proposed method is more robust and suitable to various image and video applications than the conventional segmentation methods.
2. Proposed Robust Image Segmentation Method
This work develops a robust image segmentation method based on the modified edge-following technique, where different thresholds are automatically generated according to the characteristics of local areas. Taking the "garden" image in Figure 1(a) as an example, Figure 1(b) divides this image into 16 bocks and calculates the average value of gradients between the currently processed point and its neighboring points in eight compass directions to plot a histogram of the average values from all points in each block. Looking at these histograms, the complicated part circled in the diagram represents the area of extreme changes in gradients. With a larger variation of gradients, the threshold for this area must also be larger than that adopted in the smooth area to prevent over-segmentation. To adapt to variations of gradients in each area, the quad-tree decomposition is adopted to divide an image into four blocks at an equal size and would continue to divide further depending on complexities of the blocks. If the criteria for further decomposition are satisfied, then the block or subblock is divided into four subblocks or smaller subblocks; otherwise, it would stop here. The proposed decomposition would continue until all blocks and subblocks are completely obtained, as shown in Figure 2. During the quad-tree decomposition process, different threshold values can be determined for each decomposed block, according to variations in the gradients of each decomposed block, to attain accurate segmentation results. The major differences between the proposed robust image segmentation method and our previous work [15] are quad-tree decomposition, adaptive thresholds in each decomposed blocks, and direction judgment in the edge following. To clearly illustrate the proposed method, four stages are introduced. First, the iterative threshold selection technique is modified to calculate the initial-point threshold of the whole image or a particular block from the quad-tree decomposition. Second, the quad-tree decomposition is applied to establish decomposed blocks, where gray-level gradient characteristics in each block are computed for deciding further decomposition or not. After the quad-tree decomposition, the contour threshold of each decomposed block is calculated in the third stage. Initial-point thresholds are used to determine the initial points while contour thresholds can eliminate inappropriate contours to increase the accuracy of search and minimize the required searching time. Finally, the modified edge-following method is used to discover complete contours of objects. Details of each stage are described below.
2.1. Stage of Applying the Modified Iterative Threshold Selection Technique
In this stage, the gradient between the currently processed point  and its neighboring point in one of eight compass directions is first determined by using the following equation:
and its neighboring point in one of eight compass directions is first determined by using the following equation:

where  neighbors to
neighbors to  in direction
in direction  , and
, and  and
and  denote the gray-level values at locations
denote the gray-level values at locations  and
and  , respectively. Here,
, respectively. Here,  is a value denoting one of the eight compass directions as shown in Figure 3. For
is a value denoting one of the eight compass directions as shown in Figure 3. For  , the remainder of
, the remainder of  divided by 8 is taken. When
divided by 8 is taken. When  ,
,  is added by a multiple of 8 to become a positive value smaller than 8. Hence, "1", "9", and "
is added by a multiple of 8 to become a positive value smaller than 8. Hence, "1", "9", and " 7" denote the same directions. This will be useful in Section 2.4.
7" denote the same directions. This will be useful in Section 2.4.
 is defined to take a mean of
is defined to take a mean of  in eight directions for the point
in eight directions for the point  in the following equation:
in the following equation:

The iterative threshold selection technique that was proposed by Ridler and Calvard to segment the foreground and background is modified to calculate the initial-point threshold of the whole image or a particular block from the quad-tree decomposition, for identifying initial points [35]. The modified iterative threshold selection technique is illustrated as follows.
-
(1)
Let
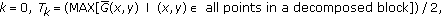 where MAX is a function to select the maximum value.
where MAX is a function to select the maximum value. -
(2)
 is adopted to classify all points in a decomposed block into initial and noninitial points. A point with
is adopted to classify all points in a decomposed block into initial and noninitial points. A point with  is an initial point, while a point with
is an initial point, while a point with 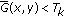 is a noninitial point. The groups of initial and noninitial points are denoted by
is a noninitial point. The groups of initial and noninitial points are denoted by  and
and 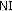 , respectively. In these two groups, the averaged
, respectively. In these two groups, the averaged  is computed by
is computed by (3)
(3)where
 and
and 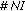 denote the numbers of initial and noninitial points, respectively,
denote the numbers of initial and noninitial points, respectively, -
(3)
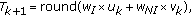 (4)
(4)where round
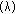 rounds off the value of
rounds off the value of 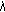 to the nearest integer number.
to the nearest integer number.  and
and  , ranging from 0 to 1, denote the weighting values of initial and noninitial groups, respectively. Additionally,
, ranging from 0 to 1, denote the weighting values of initial and noninitial groups, respectively. Additionally, 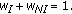
-
(4)
If
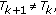 then
then 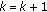 and go to Step 2, else
and go to Step 2, else 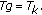
Notably,  is limited to the range between 0 and 255, and rounded off into a specific integer in the iterative procedure so that the above-mentioned iteration always converges. Usually,
is limited to the range between 0 and 255, and rounded off into a specific integer in the iterative procedure so that the above-mentioned iteration always converges. Usually,  and
and  are set to 0.5 to allow
are set to 0.5 to allow  locating in the middle of two groups. To avoid missing some initial points in low-contrast areas of an image with complicated contents,
locating in the middle of two groups. To avoid missing some initial points in low-contrast areas of an image with complicated contents,  can be increased to lower
can be increased to lower  . However, with an increasing decomposition level in the quad-tree decomposition process,
. However, with an increasing decomposition level in the quad-tree decomposition process,  can be lowered for a small decomposed block that has a consistent contrast. Taking the "alumgrns" image in Figure 4 as an example, the initial-point threshold
can be lowered for a small decomposed block that has a consistent contrast. Taking the "alumgrns" image in Figure 4 as an example, the initial-point threshold  of the entire image calculated by the modified iterative threshold selection is 16 under
of the entire image calculated by the modified iterative threshold selection is 16 under  The rough contour formed by initial points can be found as depicted in Figure 4(b), but the contour is not intact. Hence, the quad-tree decomposition in the following stage would take this
The rough contour formed by initial points can be found as depicted in Figure 4(b), but the contour is not intact. Hence, the quad-tree decomposition in the following stage would take this  as the basis to compute the initial-point threshold value of each decomposed block depending on the complexity of each area.
as the basis to compute the initial-point threshold value of each decomposed block depending on the complexity of each area.
2.2. Stage of the Quad-Tree Decomposition Process
In this stage, the whole image is partitioned into many blocks by using quad-tree decomposition. The quad-tree decomposition process starts with the initial-point threshold, mean and standard deviations derived from the entire image on the top level. At each block, the process determines the initial-point threshold and whether this block should be further decomposed. For the whole image or each block, Figure 5 shows the flow chart of the quad-tree decomposition to determine whether the currently processed block is further decomposed and to calculate the initial-point threshold of this block. Assume that the block  with a mean
with a mean  and a standard deviation
and a standard deviation  of gray-level gradients is currently processed. The parent block of
of gray-level gradients is currently processed. The parent block of  is represented by
is represented by  in which initial-point threshold, mean and standard deviations are denoted by
in which initial-point threshold, mean and standard deviations are denoted by  ,
,  and
and  , respectively. While
, respectively. While  of each point in the block
of each point in the block  is smaller than
is smaller than  , the block
, the block  does not contain any initial point and thus its initial-point threshold
does not contain any initial point and thus its initial-point threshold  is set to
is set to  in order to avoid the initial-point generation. Under such a situation, there is no further decomposition in the block
in order to avoid the initial-point generation. Under such a situation, there is no further decomposition in the block  . On the other hand, when
. On the other hand, when  of any point of the block
of any point of the block  is larger than
is larger than  , the block
, the block  is further decomposed into four subblocks. Additionally,
is further decomposed into four subblocks. Additionally,  is temporarily given by the value computed by the modified iterative threshold selection technique in the block
is temporarily given by the value computed by the modified iterative threshold selection technique in the block  . If
. If  and
and  , then the block
, then the block  would contain a smoother area than the block
would contain a smoother area than the block  . Let
. Let  to prevent the reduction of the initial-point threshold from yielding the undesired initial points. If
to prevent the reduction of the initial-point threshold from yielding the undesired initial points. If  and
and  , the complexity of the block
, the complexity of the block  is increased. In this situation, the block
is increased. In this situation, the block  may contain contour points, but may also include many undesired noises or complicated image contents. Hence, raising the initial-point threshold by
may contain contour points, but may also include many undesired noises or complicated image contents. Hence, raising the initial-point threshold by  to allow that
to allow that  can eliminate the noises and reduce the over-segmentation result in the block
can eliminate the noises and reduce the over-segmentation result in the block  . Otherwise, the initial point threshold
. Otherwise, the initial point threshold  of the block
of the block  that may contain objects is remained as the value from the modified iterative threshold selection technique conducted in the block
that may contain objects is remained as the value from the modified iterative threshold selection technique conducted in the block  .
.
During the quad-tree decomposition process,  can be set by a value smaller than 0.5 at the first decomposition level to lower
can be set by a value smaller than 0.5 at the first decomposition level to lower  for capably attaining initial points from low-contrast areas. Additionally,
for capably attaining initial points from low-contrast areas. Additionally,  is increased with a decomposition level. For the smallest decomposed block in the last decomposition level,
is increased with a decomposition level. For the smallest decomposed block in the last decomposition level,  can be a value larger than or equal to 0.5 for increasing
can be a value larger than or equal to 0.5 for increasing  to avoid the undesired initial points. Notably, the initial-point thresholds of blocks with drastic gray-level changes would rise, whereas the initial-point thresholds of blocks with smooth gray-level changes would fall. This approach of determining initial-point threshold can obtain adequate initial points based on the complexity of image contents.
to avoid the undesired initial points. Notably, the initial-point thresholds of blocks with drastic gray-level changes would rise, whereas the initial-point thresholds of blocks with smooth gray-level changes would fall. This approach of determining initial-point threshold can obtain adequate initial points based on the complexity of image contents.
After the quad-tree decomposition is finished, the positions and moving directions of initial points in each block are recorded accordingly.
-
(1)
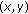 is a point from a decomposed block
is a point from a decomposed block 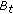 .
. -
(2)
If
 then
then 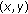 is labeled as the initial point and
is labeled as the initial point and 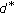 is recorded where
is recorded where 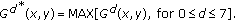
-
(3)
Repeat step 2 for all points in the block
 .
.
2.3. Stage of Determining the Contour Threshold Tc
At the end of the quad-tree decomposition process, the gradients of each decomposed block are computed to determine the contour threshold  . According to (1), the largest value of
. According to (1), the largest value of  in the eight directions is
in the eight directions is  , where
, where  is a specific value of
is a specific value of  for yielding the maximum
for yielding the maximum  . The histogram of
. The histogram of  from all points of the decomposed block is calculated. Here,
from all points of the decomposed block is calculated. Here,  is assumed to be the number of the absolute gray-level difference being
is assumed to be the number of the absolute gray-level difference being  . If a decomposed block comprises many one-pixel lines that are all black and white in an interlaced manner, then this decomposed block contains the maximum number of contour points, which is half the number of points in the decomposed block. Restated, the first half of the histogram results from noncontour points at least. Accordingly, the contour threshold
. If a decomposed block comprises many one-pixel lines that are all black and white in an interlaced manner, then this decomposed block contains the maximum number of contour points, which is half the number of points in the decomposed block. Restated, the first half of the histogram results from noncontour points at least. Accordingly, the contour threshold  can be the index value, indicating that
can be the index value, indicating that  denotes half the number of points in a decomposed block, as indicated in Figure 6. This threshold does not miss any contour points. When the search is conducted for contour points,
denotes half the number of points in a decomposed block, as indicated in Figure 6. This threshold does not miss any contour points. When the search is conducted for contour points,  is used to determine whether to stop the search procedure in the modified edge-following scheme. If the differences between the predicted contour point and its left and right neighboring points are less than
is used to determine whether to stop the search procedure in the modified edge-following scheme. If the differences between the predicted contour point and its left and right neighboring points are less than  , then the search has taken the wrong path, and should stop immediately. This approach not only prevents searching in the wrong path, but also saves on the search time. Additionally,
, then the search has taken the wrong path, and should stop immediately. This approach not only prevents searching in the wrong path, but also saves on the search time. Additionally,  of each decomposed block is independently determined to adapt to the characteristics of each area.
of each decomposed block is independently determined to adapt to the characteristics of each area.
2.4. Stage of Applying the Modified Edge-Following Method
The initial-point threshold  , contour threshold
, contour threshold  , and initial points are obtained in the previous stages. In this stage, the searching procedure is started from each initial point until the closed-loop contour is found. The position and direction of the
, and initial points are obtained in the previous stages. In this stage, the searching procedure is started from each initial point until the closed-loop contour is found. The position and direction of the  th searched contour point are represented by
th searched contour point are represented by  and
and  , respectively. The modified edge-following method is given as follows.
, respectively. The modified edge-following method is given as follows.
-
(1)
Select an initial point and its
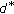 . This initial point is represented by
. This initial point is represented by  and set
and set  where the edge-following direction
where the edge-following direction 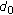 is perpendicular to the maximum-gradient direction
is perpendicular to the maximum-gradient direction 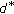 . Here,
. Here,  is a value denoting one of the eight compass directions as shown in Figure 3.
is a value denoting one of the eight compass directions as shown in Figure 3. -
(2)
Let
 , where
, where 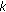 is the contour-point index. The searching procedure begins from the initial point
is the contour-point index. The searching procedure begins from the initial point 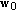 and the direction
and the direction  .
. -
(3)
First, to reduce computational time, the search is restricted to only three directions by setting
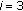 , where
, where  denotes the number of directions needed. The direction
denotes the number of directions needed. The direction 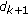 of the next point thus has three possible values:
of the next point thus has three possible values: 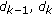 and
and  . For instance, if
. For instance, if 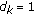 , then the next contour point
, then the next contour point  could appear at the predicted contour point
could appear at the predicted contour point 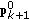 ,
,  or
or 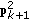 , as shown in Figure 7(a). With the left-sided point
, as shown in Figure 7(a). With the left-sided point 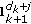 and right-sided point
and right-sided point  of the predicted contour point
of the predicted contour point 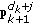 , the line formed by
, the line formed by 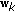 and
and  points is perpendicular to the line between
points is perpendicular to the line between 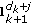 and
and 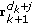 , where
, where  indicates the direction deviation, as revealed in Figure 7(b) under
indicates the direction deviation, as revealed in Figure 7(b) under  and
and 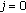 . Additionally,
. Additionally, 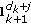 and
and 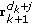 can be represented as
can be represented as  (5)
(5)
respectively, where  ranges from
ranges from  to
to  , round
, round rounds off the value of
rounds off the value of  to the nearest integer number.
to the nearest integer number.
-
(4)
The gray-level average values
 and
and  of the previous contour points are calculated as
of the previous contour points are calculated as 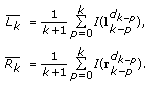 (6)
(6)
-
(5)
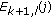 and
and 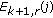 that interpret the relationships among the predicted point, its left-sided and right-sided points, and
that interpret the relationships among the predicted point, its left-sided and right-sided points, and 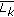 and
and 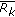 , are used to obtain the next probable contour point:
, are used to obtain the next probable contour point: 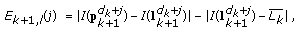 (7)
(7)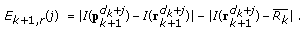 (8)
(8)Equations (7) and (8) are used to determine the
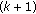 th contour point. The first term represents the gradient between the predicted point and its left-sided or right-sided point. The second term may prevent (7) or (8) from finding the wrong contours due to the noise interference. If the difference in the second term is too large, then the wrong contour point may be found.
th contour point. The first term represents the gradient between the predicted point and its left-sided or right-sided point. The second term may prevent (7) or (8) from finding the wrong contours due to the noise interference. If the difference in the second term is too large, then the wrong contour point may be found. -
(6)
Select the largest value by using
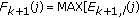 or
or  If
If  , then the correct direction has been found, and go to step 8. Here,
, then the correct direction has been found, and go to step 8. Here,  comes from the decomposed block which the predicted contour point
comes from the decomposed block which the predicted contour point 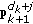 belongs to.
belongs to. -
(7)
If
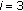 , then the previously searched direction may have deviated from the correct path and set
, then the previously searched direction may have deviated from the correct path and set  to obtain the seven neighboring points for direction searching, going to step 5. Otherwise, stop the search procedure, and go to step 10.
to obtain the seven neighboring points for direction searching, going to step 5. Otherwise, stop the search procedure, and go to step 10. -
(8)
From
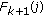 , the correct direction
, the correct direction  and position of the
and position of the  th contour point are calculated as follows:
th contour point are calculated as follows:  (9)
(9)
-
(9)
The searching procedure is finished when the
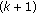 th contour point is in the same position as any of the previous searched contour points or has gone beyond the four boundaries of the image. If neither condition is true, then set
th contour point is in the same position as any of the previous searched contour points or has gone beyond the four boundaries of the image. If neither condition is true, then set 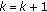 , and return to step 3 to discover the next contour point.
, and return to step 3 to discover the next contour point. -
(10)
If
 set
set 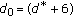 and go to step 2 to search for the contour points in the opposite direction to
and go to step 2 to search for the contour points in the opposite direction to 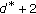 .
. -
(11)
Go to step 1 for another initial point that is not searched. When all initial points are conducted, the procedure of the modified edge-following method is ended.
During the searching process, taking in the left and right neighboring points of the next predicted contour point in computation would significantly reduce the tendency of the edge-following method to deviate from the correct edge due to noise interferences. Only three directions are first searched in the searching process. If the  values of these three directions are all below
values of these three directions are all below  , then the search proceeds to the seven directions. The searching time is thus significantly decreased, since most searches only need the computation of the gradients in three directions. Figure 8 depicts the flow chart of the proposed modified edge-following scheme that searches from an initial point.
, then the search proceeds to the seven directions. The searching time is thus significantly decreased, since most searches only need the computation of the gradients in three directions. Figure 8 depicts the flow chart of the proposed modified edge-following scheme that searches from an initial point.
3. Computational Analyses
In the following experiment, the LWOF, E-GVF snake, watershed and proposed methods are adopted and compared in processing time and segmentation accuracy. Among these methods, LWOF is a supervised segmentation method, with small circles indicating the positions selected by the user for segmentation. The user can adequately select some points close to an object to obtain a segmentation result that is closest to that observed with naked eyes. However, LWOF requires a very long computational time, and is dependent on the user. Consequently, the processing time of LWOF must include the manual operational time. The segmentation function adopted by the watershed method is gradient [9]. Additionally, the merging operation is based on the region mean where the threshold indicates the criterion of region merging. Here, two quantities, precision and recall, are employed to evaluate the segmented results from each segmentation method [34, 36]. Precision,  , is the probability that a detected pixel is a true one. Recall,
, is the probability that a detected pixel is a true one. Recall,  , is the probability that a true pixel is detected:
, is the probability that a true pixel is detected:

Additionally, the F-measure,  , with considering
, with considering  and
and  is adopted and defined as
is adopted and defined as

where α is set to 0.5 in our simulations.
Figure 9(a) shows a 256 × 256-pixel "bacteria" image, which includes about 20 bacteria objects that do not overlap with each other. The shot was taken out of focus, causing the image edges to be blurry, thus affecting some of the segmented results. Figure 9(b) displays the result from LWOF. LWOF takes a long time because it must perform about 20 object selection operations. Figure 9(c) depicts the result from the E-GVF snake method. Some groups of connected neighboring bacteria objects are mistaken for single objects. Figures 9(d) and 9(e) show the results from utilizing the watershed method with thresholds of 20 and 40, respectively. Many erroneous borders are found when the threshold is 20, with some single objects being segmented into multiple smaller parts. While fewer erroneous contours are found when the threshold is 40, some objects are still missing. The number of missing objects increases with the threshold. Contrasts in this picture are significantly reduced owing to the unfocused image, making the threshold hard to adjust. An excessively large threshold causes missing objects, but a very small threshold would cause the background to blur with the bacteria, which make it even more difficult to segment. To do fair comparison, the watershed method is iteratively conducted under different thresholds to yield the best segmented results in the following analyses. Figure 9(f) displays the results from the proposed method, which is not affected by the out-of-focus image due to adequate initial points attained, and thus can segment every bacteria object.
Segmented results of the "bacteria" image. (a) Original image. (b) Result obtained by the LWOF method. (c) Result obtained by the E-GVF snake method. (d) Result obtained by the watershed method with a threshold of 20. (e) Result obtained by the watershed method with a threshold of 40. (f) Result obtained by the proposed method.
Figure 10(a) shows the 540 × 420-pixel "chessboard" image, which is a 3D manmade image including a chessboard and cylinders. The light effect is added in the picture, reflecting shadows of the cylinders on the chessboard. Figure 10(b) shows the ground truth from Figure 10(a). The result from LWOF is depicted in Figure 10(c). A fairly good result is obtained using the manual operation, but a large number of initial points required means that the computational time is very long. Figure 10(d) displays the result from the E-GVF snake method, which is clearly not appropriate for an image, with objects all very close to each other. The simulation result indicates that contour of the outermost layer is segmented, but that the squares inside the chessboard cannot be detached from each other, leaving the result with only one object. Figure 10(e) shows results from using the watershed method at a threshold being 27 with the maximum F-measure. Figure 10(f) depicts the result from the proposed method. The proposed method not only can segment the two letters and the cylinders, it also segments the chessboard itself better than does the watershed method with the best threshold value. The segmentation of the side surface in the chessboard is also far more accurate than that generated from the watershed method. Table 1 lists the segmentation results from the LWOF, E-GVF snake, watershed at a threshold with the maximum F-measure, and proposed methods. Objects from the picture include two areas of cylinders, 24 areas of the chessboard's top side, letters "A" and "B", and 10 areas of the chessboard's front and right sides, for a total of 36 close-looped independent areas. While the supervised LWOF method has the highest F-measure, it also requires a long time. Amongst the unsupervised methods, the proposed method can segment the most objects, and also has a significantly higher F-measure than the E-GVF snake and watershed methods.
Figure 11 shows the 360 × 360-pixel "square" image corrupted by the Gaussian noise, at the Signal-to-Noise Ratio (SNR) of 18.87 dB. Figures 11(a) and 11(b) depict the noisy image and ground truth, respectively. The result from adopting the LWOF segmentation is displayed in Figure 11(c). Not many points are selected manually since the angles of turns are not very large. However, the contour is not smooth due to the noise. Figure 11(d) shows the result obtained by using the E-GVF snake method. Some dark areas could be lost in the sharp corners. The result from using the watershed method at a threshold being 45 with the maximum F-measure is depicted in Figure 11(e). The proposed method can eliminate the problem and obtain the correct area as shown in Figure 11(f). Table 2 compares F-measures and computational time of the four segmentation methods at SNRs of 18.87 dB, 12.77 dB and 9.14 dB in which the watershed method adopts thresholds of 42, 44, and 45, respectively. By using the proposed method, the segmented area has the highest F-measures in each of the three SNR scenarios. The proposed method using the modified edge-following technique is significantly faster than LWOF when the manual operational time is considered. Additionally, the proposed method provides comparable or even better results than the LWOF. The results obtained by the watershed method at thresholds with the maximum F-measures take slightly lower processing time than the proposed method when the threshold selection time is not counted in the watershed method. The above experiments were conducted by using C programs running on a Pentium IV 2.4 GHz CPU under Windows XP operating system.
Segmented results of the "square" image added by noises with the Gaussian distribution at SNR of 18. 87 dB. (a) Noisy image. (b) Ground truth. (c) Result obtained by the LWOF method. (d) Result obtained by the E-GVF snake method. (e) Result obtained by the watershed method with a threshold of 45. (f) Result obtained by the proposed method.
The above experimental results demonstrate that the proposed method performs better than the other methods. As for the blurry objects resulting from the out-of-focus shot in Figure 9, the proposed method can accurately segment all objects without incurring over-segmentation and under-segmentation as does the watershed method in Figures 9(d) and 9(e), respectively. Figure 10 reveals that both the proposed and watershed methods demonstrate the capability of fully segmenting objects inside another object and overlapping objects but the E-GVF snake method cannot be applied in these pictures. The proposed method can segment more objects out of the image in Figure 10, which contains many individual objects, than the watershed method. In the simulation results shown in Figure 11, by considering the gray-level changes of the left and right neighboring points during the contour-searching process, the proposed method not only reduces the noise interference, it also outperforms both the E-GVF snake and watershed methods against noise interference.
To do fair comparison, the data set and benchmarks from the Computer Vision Group, University of California at Berkeley were applied in the proposed and watershed methods, where the watershed method is also iteratively performed to search for the optimized threshold. Since the E-GVF snake method is not suitable for the image with objects inside another object, it is not addressed in this data set. The segmentation results of the conventional methods such as Brightness Gradient (BG), Texture Gradient (TG), and Brightness/Texture Gradients (B/TG) are referred from [34] for comparison. The precision-recall ( ) curve shows the inherent trade-off between
) curve shows the inherent trade-off between  and
and  . Figure 12 depicts the segmented results and the precision-recall curves from Human, BG, TG, B/TG, watershed and proposed methods. In Figures 12(c), 12(d), 12(e), and 12(f), the BG, TG, B/TG and watershed methods are iteratively conducted under different thresholds to yield the best segmented results with
. Figure 12 depicts the segmented results and the precision-recall curves from Human, BG, TG, B/TG, watershed and proposed methods. In Figures 12(c), 12(d), 12(e), and 12(f), the BG, TG, B/TG and watershed methods are iteratively conducted under different thresholds to yield the best segmented results with  of 0.87, 0.88, 0.88, and 0.83, respectively. In the proposed method, the threshold is automatically determined to be a specific value that only yields a converged point in Figure 12(g), where the F-measure of 0.93 can be achieved. Hence, the proposed method does not need the ground truth to iteratively determine the best-matched thresholds and thereby greatly reduces the computational time demanded by the BG, TG, B/TG, and watershed methods.
of 0.87, 0.88, 0.88, and 0.83, respectively. In the proposed method, the threshold is automatically determined to be a specific value that only yields a converged point in Figure 12(g), where the F-measure of 0.93 can be achieved. Hence, the proposed method does not need the ground truth to iteratively determine the best-matched thresholds and thereby greatly reduces the computational time demanded by the BG, TG, B/TG, and watershed methods.
The proposed method is applied to all test images, and its segmentation results are evaluated according to the ground truths. Particularly, six images from 100 test images are added by the Gaussian noise to become noisy images at the SNR of 18.87 dB. Figure 13 displays the segmented results of original and noisy images using the proposed and watershed methods, where F-measures and computational time are listed in Table 3. From Figure 13, the segmented results from the proposed method exhibit more apparent and complete objects than those from the watershed method at specific thresholds with the maximum F-measures. In Figures 13(a), 13(b), 13(c), 13(d), 13(e), and 13(f), the watershed method is conducted under thresholds of 23, 30, 7, 45, 16, and 32 to yield the best segmented results, respectively. Additionally,  curves from proposed and watershed methods are depicted. Moreover, the proposed method with thresholds adapting to image contents has higher or equal F-measure values than the watershed methods as illustrated in Table 3. Regarding to computational time, the proposed method at most cases takes slightly longer time than the watershed method owing to additional threshold determination process required by the proposed method when the iterative process of determining the best threshold of the watershed method is not included.
curves from proposed and watershed methods are depicted. Moreover, the proposed method with thresholds adapting to image contents has higher or equal F-measure values than the watershed methods as illustrated in Table 3. Regarding to computational time, the proposed method at most cases takes slightly longer time than the watershed method owing to additional threshold determination process required by the proposed method when the iterative process of determining the best threshold of the watershed method is not included.
Original image, noisy image, segmented noisy image from the proposed method, segmented noisy image from the watershed method at a threshold with the maximum F-measure,  curve by using the proposed method,
curve by using the proposed method,  curve by using the watershed method, displaying from left to right in two rows. (a) 78004th image. (b) 21077th image. (c) 210088th image. (d) 300091st image. (e) 271035th image. (f) 219090th image.
curve by using the watershed method, displaying from left to right in two rows. (a) 78004th image. (b) 21077th image. (c) 210088th image. (d) 300091st image. (e) 271035th image. (f) 219090th image.
The histograms of F-measures from 100 test images by using BG, TG, B/TG, and proposed method are shown in Figure 14. Although the proposed method yields little poor performance in few images under very low contrast, it still has above 0.6 of F-measure for 70 test images. The number of F-measures between 0.6 and 0.9 in the proposed method is 68 larger than 64 in BG and 59 in TG, and smaller than 73 in B/TG while the number of F-measures between 0.9 and 1.0 in the proposed method is 2 better than none in BG, TG, and B/TG. Restated, when the images have apparent contours, the proposed method can yield segmented results close to the ground truth done by humans. The proposed method can effectively determine the main foreground and is not trapped to the complex background. Hence, the values of  in these cases under the proposed method can be superior to those using the conventional methods. From computational time point of view, the proposed method that uses automatically determined thresholds to perform image segmentation apparently takes the least time than the conventional methods that are iteratively conducted under different thresholds to converge their minima.
in these cases under the proposed method can be superior to those using the conventional methods. From computational time point of view, the proposed method that uses automatically determined thresholds to perform image segmentation apparently takes the least time than the conventional methods that are iteratively conducted under different thresholds to converge their minima.
In practical applications, the ground truths are not available. The conventional methods, BG, TG, and B/TG, that need the ground truths to determine the best-matched thresholds or parameters may not obtain good segmentation results under no ground truth. However, the proposed robust segmentation method does not need the ground truths and iterative operations to determine the segmentation results, and therefore is very suitable to various real-time image and video segmentation applications under no ground truth.
4. Conclusion
This work proposes an automatically determined threshold mechanism to perform a robust segmentation. Different initial-point thresholds are determined and given to areas with drastic and smooth changes in gray-level values. The contour thresholds are generated by analyzing the decomposed blocks, thus preventing the search from falling into the wrong path, and saving computational time. The contour search process also considers the gradients of the left and right neighboring points of every predicted contour point, in order to lower the possibility of the method being affected by the neighboring noise interferences. Additionally, most of the searching process requires only the computation of the gradients of three directions, thus minimizing the searching time. The proposed method can perform segmentation on objects inside another object and objects that are close to each other, which the E-GVF snake method cannot perform. The proposed method also solves problems encountered by the watershed method, in which the results may change significantly as the threshold values differ. The proposed method can significantly reduce noise interference, which easily affects the conventional edge-following method. In handling blurry objects from an out-of-focus shot, the proposed method can also segment the required objects. Finally, the benchmark from Computer Vision Group, University of California at Berkeley was conducted to demonstrate that the proposed method could take the least computational time to obtain robust and good segmentation performance than the conventional ones. Therefore, the proposed method can be widely and effectively employed in various segmentation applications.
References
Liu D, Chen T: DISCOV: a framework for discovering objects in video. IEEE Transactions on Multimedia 2008,10(2):200-208.
Pan J, Gu C, Sun MT: An MPEG-4 virtual video conferencing system with robust video object segmentation. Proceedings of Workshop and Exhibition on MPEG-4, June 2001, San Jose, Calif, USA 45-48.
Yang J-F, Hao S-S, Chung P-C, Huang C-L: Color object segmentation with eigen-based fuzzy C-means. Proceedings of the IEEE International Symposium on Circuits and Systems (ISCAS '00), May 2000, Geneva, Switzerland 5: 25-28.
Chien S-Y, Huang Y-W, Hsieh B-Y, Ma S-Y, Chen L-G: Fast video segmentation algorithm with shadow cancellation, global motion compensation, and adaptive threshold techniques. IEEE Transactions on Multimedia 2004,6(5):732-748. 10.1109/TMM.2004.834868
Zhou JY, Ong EP, Ko CC: Video object segmentation and tracking for content-based video coding. Proceedings of IEEE International Conference on Multimedia and Expo (ICME '00), July 2000, New York, NY, USA 3: 1555-1558.
Chiang C-C, Hung Y-P, Lee GC: A learning state-space model for image retrieval. EURASIP Journal on Advances in Signal Processing 2007, 2007:-10.
Chen YB, Chen OT-C, Chang HT, Chien JT: An automatic medical-assistance diagnosis system applicable on X-ray images. Proceedings of the 44th IEEE Midwest Symposium on Circuits and Systems (MWSCAS '01), August 2001, Dayton, Ohio, USA 2: 910-914.
Nock R, Nielsen F: Semi-supervised statistical region refinement for color image segmentation. Pattern Recognition 2005,38(6):835-846. 10.1016/j.patcog.2004.11.009
Vincent L, Soille P: Watersheds in digital spaces: an efficient algorithm based on immersion simulations. IEEE Transactions on Pattern Analysis and Machine Intelligence 1991,13(6):583-598. 10.1109/34.87344
Adams R, Bischof L: Seeded region growing. IEEE Transactions on Pattern Analysis and Machine Intelligence 1994,16(6):641-647. 10.1109/34.295913
Kim DH, Yun ID, Lee SU: New MRF parameter estimation technique for texture image segmentation using hierarchical GMRF model based on random spatial interaction and mean field theory. Proceedings of the 18th International Conference on Pattern Recognition (ICPR '06), August 2006, Hong Kong 2: 365-368.
Canny J: Computational approach to edge detection. IEEE Transactions on Pattern Analysis and Machine Intelligence 1986,8(6):679-698.
Bogdanova I, Bresson X, Thiran J-P, Vandergheynst P: Scale space analysis and active contours for omnidirectional images. IEEE Transactions on Image Processing 2007,16(7):1888-1901.
Pitas I: Digital Image Processing Schemes and Application. John Wiley & Sons, New York, NY, USA; 2000.
Chen YB, Chen OT-C: Robust fully-automatic segmentation based on modified edge-following technique. Proceedings of IEEE International Conference on Acoustics, Speech, and Signal Processing (ICASSP '03), April 2003, Hong Kong 3: 333-336.
Sonka M, Hlavac V, Boyle R: Image Processing, Analysis, and Machine Vision. 2nd edition. Brooks/Cole, New York, NY, USA; 1998.
Chien S-Y, Huang Y-W, Chen L-G: Predictive watershed: a fast watershed algorithm for video segmentation. IEEE Transactions on Circuits and Systems for Video Technology 2003,13(5):453-461. 10.1109/TCSVT.2003.811605
Kuo CJ, Odeh SF, Huang MC: Image segmentation with improved watershed algorithm and its FPGA implementation. Proceedings of the IEEE International Symposium on Circuits and Systems (ISCAS '01), May 2001, Sydney, Australia 2: 753-756.
Grau V, Mewes AUJ, Alcañiz M, Kikinis R, Warfield SK: Improved watershed transform for medical image segmentation using prior information. IEEE Transactions on Medical Imaging 2004,23(4):447-458. 10.1109/TMI.2004.824224
Hu Y, Nagao T: A matching method based on marker-controlled watershed segmentation. Proceedings of the International Conference on Image Processing (ICIP '04), October 2004, Singapore 1: 283-286.
Salembier P, Garrido L: Binary partition tree as an efficient representation for image processing, segmentation, and information retrieval. IEEE Transactions on Image Processing 2000,9(4):561-576. 10.1109/83.841934
Lu H, Woods JC, Ghanbari M: Binary partition tree for semantic object extraction and image segmentation. IEEE Transactions on Circuits and Systems for Video Technology 2007,17(3):378-383.
Falcao AX, Udupa JK, Miyazawa FK: An ultra-fast user-steered image segmentation paradigm: live wire on the fly. IEEE Transactions on Medical Imaging 2000,19(1):55-62. 10.1109/42.832960
Kass M, Witkin A, Terzopoulos D: Snakes: active contour models. International Journal of Computer Vision 1988,1(4):321-331. 10.1007/BF00133570
Yu SX: Segmentation using multiscale cues. Proceedings of IEEE Computer Society Conference on Computer Vision and Pattern Recognition (CVPR '04), June-July 2004, Washington, DC, USA 1: 247-254.
Paragios N, Deriche R: Geodesic active contours and level sets for the detection and tracking of moving objects. IEEE Transactions on Pattern Analysis and Machine Intelligence 2000,22(3):266-280. 10.1109/34.841758
Mukherjee DP, Ray N, Acton ST: Level set analysis for leukocyte detection and tracking. IEEE Transactions on Image Processing 2004,13(4):562-572. 10.1109/TIP.2003.819858
Chuang C-H, Lie W-N: A downstream algorithm based on extended gradient vector flow field for object segmentation. IEEE Transactions on Image Processing 2004,13(10):1379-1392. 10.1109/TIP.2004.834663
Kim B-G, Park D-J: Novel noncontrast-based edge descriptor for image segmentation. IEEE Transactions on Circuits and Systems for Video Technology 2006,16(9):1086-1095.
Gao H, Siu W-C, Hou C-H: Improved techniques for automatic image segmentation. IEEE Transactions on Circuits and Systems for Video Technology 2001,11(12):1273-1280. 10.1109/76.974681
Chen YB, Chen OT-C: Semi-automatic image segmentation using dynamic direction prediction. Proceedings of the IEEE International Conference on Acoustics, Speech, and Signal Processing (ICASSP '02), May 2002, Orlando, Fla, USA 4: 3369-3372.
Tierny J, Vandeborre J-P, Daoudi M: Topology driven 3D mesh hierarchical segmentation. Proceedings IEEE International Conference on Shape Modeling and Applications (SMI '07), June 2007, Lyon, France 215-220.
Smith JR, Chang S-F: Quad-tree segmentation for texture-based image query. Proceedings of the 2nd Annual ACM Multimedia Conference, October 1994, San Francisco, Calif, USA 279-286.
Martin D, Fowlkes C, Tal D, Malik J: A database of human segmented natural images and its application to evaluating segmentation algorithms and measuring ecological statistics. Proceedings of the 8th IEEE International Conference on Computer Vision, July 2001, Vancouver, Canada 2: 416-423.
Ridler TW, Calvard S: Picture thresholding using an iterative selection method. IEEE Transactions on Systems, Man, and Cybernetics 1978,8(8):630-632.
van Rijsbergen C: Information Retrieval. 2nd edition. Department of Computer Science, University of Glasgow, Glasgow, UK; 1979.
Acknowledgments
Valuable discussions with Professor Tsuhan Chen, Carnegie Mellon University, Pittsburgh, USA is highly appreciated. Additionally, the authors would like to thank the National Science Council, Taiwan, for financially supporting this research under Contract nos.: NSC 95-2221-E-270-015 and NSC 95-2221-E-194-032. Professor W. N. Lie, National Chung Cheng University, Chiayi, Taiwan is appreciated for his valuable suggestion. Dr. C. H. Chuang, Institute of Statistical Science, Academia Sinica, Taipei, Taiwan, is thanked for kindly providing the software program of the snake and watershed methods.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Chen, Y.B., Chen, O.TC. Image Segmentation Method Using Thresholds Automatically Determined from Picture Contents. J Image Video Proc 2009, 140492 (2009). https://doi.org/10.1155/2009/140492
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1155/2009/140492



 representing eight compass directions.
representing eight compass directions.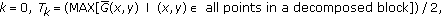 where MAX is a function to select the maximum value.
where MAX is a function to select the maximum value. is adopted to classify all points in a decomposed block into initial and noninitial points. A point with
is adopted to classify all points in a decomposed block into initial and noninitial points. A point with  is an initial point, while a point with
is an initial point, while a point with 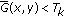 is a noninitial point. The groups of initial and noninitial points are denoted by
is a noninitial point. The groups of initial and noninitial points are denoted by  and
and 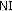 , respectively. In these two groups, the averaged
, respectively. In these two groups, the averaged  is computed by
is computed by
 and
and 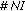 denote the numbers of initial and noninitial points, respectively,
denote the numbers of initial and noninitial points, respectively,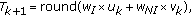
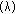 rounds off the value of
rounds off the value of 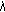 to the nearest integer number.
to the nearest integer number.  and
and  , ranging from 0 to 1, denote the weighting values of initial and noninitial groups, respectively. Additionally,
, ranging from 0 to 1, denote the weighting values of initial and noninitial groups, respectively. Additionally, 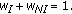
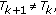 then
then 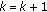 and go to Step 2, else
and go to Step 2, else 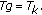

 .
.
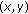 is a point from a decomposed block
is a point from a decomposed block 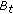 .
. then
then 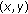 is labeled as the initial point and
is labeled as the initial point and 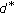 is recorded where
is recorded where 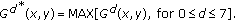
 .
.
 .
.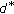 . This initial point is represented by
. This initial point is represented by  and set
and set  where the edge-following direction
where the edge-following direction 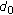 is perpendicular to the maximum-gradient direction
is perpendicular to the maximum-gradient direction 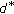 . Here,
. Here,  is a value denoting one of the eight compass directions as shown in Figure
is a value denoting one of the eight compass directions as shown in Figure  , where
, where 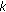 is the contour-point index. The searching procedure begins from the initial point
is the contour-point index. The searching procedure begins from the initial point 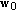 and the direction
and the direction  .
.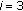 , where
, where  denotes the number of directions needed. The direction
denotes the number of directions needed. The direction 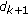 of the next point thus has three possible values:
of the next point thus has three possible values: 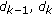 and
and  . For instance, if
. For instance, if 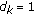 , then the next contour point
, then the next contour point  could appear at the predicted contour point
could appear at the predicted contour point 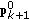 ,
,  or
or 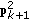 , as shown in Figure
, as shown in Figure 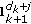 and right-sided point
and right-sided point  of the predicted contour point
of the predicted contour point 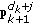 , the line formed by
, the line formed by 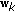 and
and  points is perpendicular to the line between
points is perpendicular to the line between 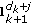 and
and 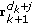 , where
, where  indicates the direction deviation, as revealed in Figure
indicates the direction deviation, as revealed in Figure  and
and 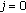 . Additionally,
. Additionally, 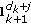 and
and 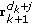 can be represented as
can be represented as 

 with its neighboring points. (a) Predicted points of
with its neighboring points. (a) Predicted points of  ,
,  and
and  under
under  . (b)
. (b)  ,
,  and
and  under
under  and
and  .
. and
and  of the previous contour points are calculated as
of the previous contour points are calculated as 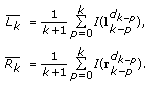
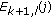 and
and 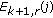 that interpret the relationships among the predicted point, its left-sided and right-sided points, and
that interpret the relationships among the predicted point, its left-sided and right-sided points, and 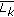 and
and 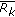 , are used to obtain the next probable contour point:
, are used to obtain the next probable contour point: 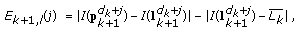
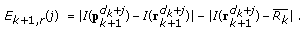
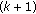 th contour point. The first term represents the gradient between the predicted point and its left-sided or right-sided point. The second term may prevent (7) or (8) from finding the wrong contours due to the noise interference. If the difference in the second term is too large, then the wrong contour point may be found.
th contour point. The first term represents the gradient between the predicted point and its left-sided or right-sided point. The second term may prevent (7) or (8) from finding the wrong contours due to the noise interference. If the difference in the second term is too large, then the wrong contour point may be found.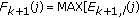 or
or  If
If  , then the correct direction has been found, and go to step 8. Here,
, then the correct direction has been found, and go to step 8. Here,  comes from the decomposed block which the predicted contour point
comes from the decomposed block which the predicted contour point  belongs to.
belongs to.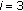 , then the previously searched direction may have deviated from the correct path and set
, then the previously searched direction may have deviated from the correct path and set  to obtain the seven neighboring points for direction searching, going to step 5. Otherwise, stop the search procedure, and go to step 10.
to obtain the seven neighboring points for direction searching, going to step 5. Otherwise, stop the search procedure, and go to step 10.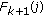 , the correct direction
, the correct direction  and position of the
and position of the  th contour point are calculated as follows:
th contour point are calculated as follows: 
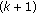 th contour point is in the same position as any of the previous searched contour points or has gone beyond the four boundaries of the image. If neither condition is true, then set
th contour point is in the same position as any of the previous searched contour points or has gone beyond the four boundaries of the image. If neither condition is true, then set 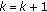 , and return to step 3 to discover the next contour point.
, and return to step 3 to discover the next contour point. set
set 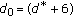 and go to step 2 to search for the contour points in the opposite direction to
and go to step 2 to search for the contour points in the opposite direction to 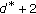 .
.





