- Research Article
- Open access
- Published:
Multiplicative Noise Removal via a Novel Variational Model
EURASIP Journal on Image and Video Processing volume 2010, Article number: 250768 (2010)
Abstract
Multiplicative noise appears in various image processing applications, such as synthetic aperture radar, ultrasound imaging, single particle emission-computed tomography, and positron emission tomography. Hence multiplicative noise removal is of momentous significance in coherent imaging systems and various image processing applications. This paper proposes a nonconvex Bayesian type variational model for multiplicative noise removal which includes the total variation (TV) and the Weberized TV as regularizer. We study the issues of existence and uniqueness of a minimizer for this variational model. Moreover, we develop a linearized gradient method to solve the associated Euler-Lagrange equation via a fixed-point iteration. Our experimental results show that the proposed model has good performance.
1. Introduction
Image denoising is an inverse problem widely studied in signal and image processing fields. The problem includes additive noise removal and multiplicative noise removal. In many image formation model, the noise is often modeling as an additive Gaussian noise: given an original image  , it is assumed that it has been corrupted by some Gaussian additive noise
, it is assumed that it has been corrupted by some Gaussian additive noise  . The denoising problem is then to recover
. The denoising problem is then to recover  from the data
from the data  . There are many effective methods to tackle this problem. Among the most famous ones are wavelets approaches [1, 2], stochastic approaches [3], principal component analysis-based approaches [4, 5], and variational approaches [6]. We refer the reader to the literature [7, 8] and references herein for an overview of the subject.
. There are many effective methods to tackle this problem. Among the most famous ones are wavelets approaches [1, 2], stochastic approaches [3], principal component analysis-based approaches [4, 5], and variational approaches [6]. We refer the reader to the literature [7, 8] and references herein for an overview of the subject.
In this paper, we focus on the issue of multiplicative noise removal. Specifically, we are interested in the denoising of SAR images. According to [9] and other references, the noise in the observed SAR image is a type of multiplicative noise which is called speckle. And the image formation model is

where  is the observed image,
is the observed image,  is the original SAR image, and
is the original SAR image, and  is the noise which follows a Gamma Law with mean one. Speckle is one of the most complex image noise models. It is signal independent, non-Gaussian, and spatially dependent. Hence speckle denoising is a very challenging problem compared with additive Gaussian noise.
is the noise which follows a Gamma Law with mean one. Speckle is one of the most complex image noise models. It is signal independent, non-Gaussian, and spatially dependent. Hence speckle denoising is a very challenging problem compared with additive Gaussian noise.
Multiplicative noise removal methods have been discussed in many reports. Popular methods include local linear minimum mean square error approaches [10, 11], anisotropic diffusion methods [12–15], and nonlocal means (NL-means) [16], which will not be addressed in this paper. We will focus on the variational approach-based multiplicative noise removal, especially that our researches will emphasis on TV-based methods.
To the best of our knowledge, there exist several variational approaches devoted to multiplicative noise removal problem. The first total variation-based multiplicative noise removal model (RLO-model) was presented by Rudin et al. [17], which used a constrained optimization approach with two Lagrange multipliers. Multiplicative model (AA-model) with a fitting term derived from a maximum a posteriori (MAP) was introduced by Aubert and Aujol [18]. Recently, Shi and Osher [19] adopted the data term of the AA-model but to replace the regularizer  by
by  . Moreover, setting
. Moreover, setting  , then they derived the strictly convex TV minimization model (SO-model). Afterwards, Huang et al. [20] modified the SO-model by adding a quadratic term to get a simpler alternating minimization algorithm. Similarly with SO-model, Bioucas and Figueiredo [21] converted the multiplicative model into an additive one by taking logarithms and proposed Bayesian type variational model. Steidl and Teuber [22] introduced a variational restoration model consisting of the I-divergence as data fitting term and the total variation seminorm as regularizer. A variational model involving curvelet coefficients for cleaning multiplicative Gamma noise was considered in [23].
, then they derived the strictly convex TV minimization model (SO-model). Afterwards, Huang et al. [20] modified the SO-model by adding a quadratic term to get a simpler alternating minimization algorithm. Similarly with SO-model, Bioucas and Figueiredo [21] converted the multiplicative model into an additive one by taking logarithms and proposed Bayesian type variational model. Steidl and Teuber [22] introduced a variational restoration model consisting of the I-divergence as data fitting term and the total variation seminorm as regularizer. A variational model involving curvelet coefficients for cleaning multiplicative Gamma noise was considered in [23].
As information carriers, all images are eventually perceived and interpreted by the human visual system. As a result, many researchers have found that human vision psychology and psychophysics play an important role in the image processing. Among them, Shen [24] has proposed Weberized TV model to remove Gaussian additive noise which incorporated the well-known psychological results—Weber's Law.
However, the previous multiplicative removal models pay a little attention to this point. Inspired by the Weberized TV regularization method [24, 25], we propose a nonconvex variational model for multiplicative noise removal. Then we prove the existence and uniqueness of a minimizer for the new model. Moreover, we develop an iterative algorithm based on the linearization technique for the associated nonlinear Euler-Lagrange equation. Our experimental results show that the proposed model has good performance.
The outline of this paper is as follows. In Section 2, we derive a new nonconvex variational model to remove multiplicative Gamma noise under the MAP framework. Moreover, we carry out the mathematic analysis of the variational model in the continuous setting. In Section 3, we develop a linearized gradient method to solve the associated Euler-Lagrange equation via a fixed-point iteration and illustrate our algorithm by displaying some numerical examples. We also compare it with other ones. Finally, concluding remarks are given in Section 4.
2. The Proposed Model and Mathematical Analysis
In this section, we propose the multiplicative noise removal model from the statistical perspective using Bayesian formulation, for which we prove the existence and uniqueness of a solution.
2.1. MAP-Based Multiplicative Noise Modeling
Let  denote
denote  -pixels instances of some random variables
-pixels instances of some random variables  and
and  . Adopting a conditionally independent multiplicative noise model, we have
. Adopting a conditionally independent multiplicative noise model, we have

where  is an image of independent and identically distributed (i.i.d) noise random variables with mean one, following Gamma density:
is an image of independent and identically distributed (i.i.d) noise random variables with mean one, following Gamma density:

After standard computation, we get

Under the MAP frameworks, the original image is inferred by solving a minimization problem with the form

We assume that  follows a Gibbs prior:
follows a Gibbs prior:  , where
, where  is a normalizing constant, and
is a normalizing constant, and  a nonnegative given function. Moreover, since
a nonnegative given function. Moreover, since  is i.i.d, therefore we have
is i.i.d, therefore we have =
=  Then, the previous computation leads us to propose the following model for restoring images corrupted with Gamma noise:
Then, the previous computation leads us to propose the following model for restoring images corrupted with Gamma noise:

Here, the first term is the image fidelity term which measures the violation of the relation between  and the observation
and the observation  . The second term is the regularization term which imposes some prior constraints on the original image and to a great degree determines the quality of the recovery image. And
. The second term is the regularization term which imposes some prior constraints on the original image and to a great degree determines the quality of the recovery image. And  is the regularization parameter which controls the tradeoff between the fidelity term and regularization term.
is the regularization parameter which controls the tradeoff between the fidelity term and regularization term.
2.2. Our Variational Model
As stated above, the choice of  is important. To the best knowledge of our known, total variational functional
is important. To the best knowledge of our known, total variational functional  has been brought into wide use ever since its introduction by Rudin et al. [6].
has been brought into wide use ever since its introduction by Rudin et al. [6].  is defined by
is defined by

which reads for  functions with weak first derivatives in
functions with weak first derivatives in  as
as

This definition for the TV functional does not require differentiability or even continuity of  . In fact one of the remarkable advantages of using TV functional for image restoration is to preserve edges due to its jump discontinuities.
. In fact one of the remarkable advantages of using TV functional for image restoration is to preserve edges due to its jump discontinuities.
As an image model,  does not take into account that our visual sensitivity to the regularity or local fluctuation
does not take into account that our visual sensitivity to the regularity or local fluctuation  depends on the ambient intensity level
depends on the ambient intensity level  [24]. Since all images are eventually perceived and interpreted by the Human Visual System (HVS), as a result, many researchers have found that human vision psychology and psychophysics play an important role in image processing. The classical example is the using of the Just Noticeable Difference Model (JND) in image coding and watermarking techniques [26, 27]. In these fields, the JND model is used to control the visual perceptual distortion during the coding procedure and watermark embedding. Weber's law was first described in 1834 by German physiologist Weber [28]. The law reveals the universal influence of the background stimulus
[24]. Since all images are eventually perceived and interpreted by the Human Visual System (HVS), as a result, many researchers have found that human vision psychology and psychophysics play an important role in image processing. The classical example is the using of the Just Noticeable Difference Model (JND) in image coding and watermarking techniques [26, 27]. In these fields, the JND model is used to control the visual perceptual distortion during the coding procedure and watermark embedding. Weber's law was first described in 1834 by German physiologist Weber [28]. The law reveals the universal influence of the background stimulus  on human's sensitivity to the intensity increment
on human's sensitivity to the intensity increment  , or so called JND, in the perception of both sound and light:
, or so called JND, in the perception of both sound and light:

According to Weber's law, when the mean intensity of the background is increasing with a higher value, then the intensity increment  also has higher value. In literature [24], the authors proposed a nonconvex variational model for additive Gaussian noise removal:
also has higher value. In literature [24], the authors proposed a nonconvex variational model for additive Gaussian noise removal:

where

The essential idea of the above model (10) is that it replaces the TV functional by the functional  , the well known perceptual law-Weber's law, in the classical TV image restoration model of Rudin et al. [6].
, the well known perceptual law-Weber's law, in the classical TV image restoration model of Rudin et al. [6].
Considering that our visual sensitivity to the local fluctuation depends on the ambient intensity level  , we take the regularization term as follows:
, we take the regularization term as follows:

According to the different purposes of image processing, we can design different  . As stated previously, we adopt
. As stated previously, we adopt  and propose the following multiplicative denoising variational model:
and propose the following multiplicative denoising variational model:

where the first two terms are the regularization terms, while the third one is the nonconvex data fidelity term following the MAP estimator for multiplicative Gamma noise.  are regularization parameters, and
are regularization parameters, and  in
in  is the given data. The first regularization term is the TV functional, which preserves important structures such as edges, an important visual cue in human and computer vision. The second term
is the given data. The first regularization term is the TV functional, which preserves important structures such as edges, an important visual cue in human and computer vision. The second term  is the well-known Weberized TV regularization term. To briefly explain the role of this term, we assume that
is the well-known Weberized TV regularization term. To briefly explain the role of this term, we assume that  has a gradient
has a gradient  , then
, then  and the Weberized local variation is
and the Weberized local variation is

which encodes the influence of the background intensity according to Weber's law (9).
The formulation (13) seems to include previous models.
-
(i)
When
 , this reduces to the SO-model [19] by letting
, this reduces to the SO-model [19] by letting  .
. -
(ii)
When
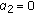 , this reduces to the AA-model [18].
, this reduces to the AA-model [18].
The current paper is devoted to the study of the mathematical properties of this new model, including issues related to the existence and uniqueness of the minimizer, and its computational approach.
2.3. Mathematical Properties of the Variational Model (13)
In this subsection, we first give the admissible space for the restoration model (13) and then investigate the existence and uniqueness of the minimizer to the model. Throughout the paper, we assume that  is a Lipschitz open domain with a finite Lebesgue measure
is a Lipschitz open domain with a finite Lebesgue measure  .
.
Since  denotes the intensity value, thus
denotes the intensity value, thus  . When
. When  , it is the singularity of both Weber's fraction (9) and the Weberized local variation (14). Hence, technically we should stay away from this point and assume that
, it is the singularity of both Weber's fraction (9) and the Weberized local variation (14). Hence, technically we should stay away from this point and assume that  .
.
First, we give the admissible space for the restoration model (13). The regularization term

can be understood in the sense of the following coarea formula.
Lemma 1.
(Coarea formula). Let  be a
be a  function and
function and  ; then
; then

Here the level set is  is the perimeter of the set
is the perimeter of the set  and the space
and the space  is of functions of bounded variation consisting of all
is of functions of bounded variation consisting of all  functions with
functions with  .
.
Proof.
Applying [26, Theorem  ], we get the conclusion.
], we get the conclusion.
From Lemma 1, we give the following nature admissible space for the restoration model (13):

When  , we note that (16) is precisely the classical co-area formula. It means that
, we note that (16) is precisely the classical co-area formula. It means that  , when
, when  . We shall work with
. We shall work with  from now on.
from now on.
Secondly, we give a theorem on the existence and uniqueness of the solution of the problem (13), respectively.
Theorem 1 (Existence).
Suppose that  with
with  ; then problem (13) has at least one minimizer in the admissible space
; then problem (13) has at least one minimizer in the admissible space  .
.
Theorem 2 (Uniqueness).
Assume that  is in
is in  , and
, and  is a minimizer of the restoration energy
is a minimizer of the restoration energy  . Then
. Then  is unique if
is unique if

For the proof of the existence and uniqueness see the appendix for details.
3. Numerical Results
In this section, we present some numerical examples to demonstrate the performance of our method. We also compare it with some existing other ones. All experiments were performed under Windows XP and MATLAB v7.1 running on a desktop with an Intel (R) Pentium (R) Dual E2180 Processor 2.00 GHZ and 0.99 GB of memory.
3.1. Algorithm
To numerically compute a solution to the problem (13), as in [24, 29, 30], we apply the linearization technique to iteratively solve the associated Euler-Lagrange equation, which we call "lagged diffusivity fixed point iteration". Since total variation functional is nonsmooth, which caused the main numerical difficulty, we replace the total variation functional by a smooth approximation like

in (13). Here  is the regularized parameter chosen near
is the regularized parameter chosen near  .
.
We first give a computational lemma.
Lemma 2.
Let  be a
be a  function and
function and

Then the formal Euler-Lagrange differential of  is
is

Proof.
Applying Green's identity, we directly compute the first Gateaux derivative of  and get the conclusion.
and get the conclusion.
Applying the above lemma to our restoration functional, the formal Euler-Lagrange equation for any solution of problem (13) is as follows

Since  , then the Euler-Lagrange equation (22) of minimizing can be rewritten equivalently as
, then the Euler-Lagrange equation (22) of minimizing can be rewritten equivalently as

Define  . Then (23) can be rewritten as
. Then (23) can be rewritten as

with the Neumann adiabatic condition along the boundary of the image domain. It is formally identical to the classical TV denoising equation [6, 29], except that the fitting constant  now depends on
now depends on  . Notice that
. Notice that  since
since  .
.
Equations: (24) can be expressed in operator notation

where  is the linear diffusion operator whose action on a function
is the linear diffusion operator whose action on a function  is given by
is given by

The fixed point iteration is then

Finite difference method is used commonly for discretization of partial differential equation (PDE). Equations (25) can be approximately computed by the first-order accurate finite difference schemes described as follows [6]:

where  . Here, we denote the space step size by
. Here, we denote the space step size by  . These schemes yield approximate form of (26):
. These schemes yield approximate form of (26):

and matrix operators  (cf. (25)) which are symmetric and positive definite and sparse. In our computational experiments,
(cf. (25)) which are symmetric and positive definite and sparse. In our computational experiments,  is set to be
is set to be  .
.
What follows is a generic algorithm for the minimization of  in (13). The superscript
in (13). The superscript  denotes iteration count.
denotes iteration count.  are user-defined tolerance,
are user-defined tolerance,  is an iteration limit, and
is an iteration limit, and  denotes the
denotes the  norm.
norm.
Input:  .
.
Initialization:  .
.
 (1) Compute a descent direction
(1) Compute a descent direction  for
for  at
at  .
.
 (2)
(2)  .
.
 (3) Check stopping criteria (see [29]):
(3) Check stopping criteria (see [29]):  or
or  or
or  .
.
In step 1, we set  and yield
and yield

Equation (30) follows from (27) and (24), respectively. The conjugate gradient method applied to solve the above linear diffusion equations to get the  and the stopping criterion of the inner conjugate gradient iteration is that the residual should be less than
and the stopping criterion of the inner conjugate gradient iteration is that the residual should be less than  . In our computational experiments, we set
. In our computational experiments, we set  , and
, and  .
.
3.2. Parameters Choice
We remark that there are two regularization parameters  and
and  in the proposed algorithm, which controls the tradeoff between the image fidelity term and the regularization term. When
in the proposed algorithm, which controls the tradeoff between the image fidelity term and the regularization term. When  , we note that our model (13) is the AA-model [18] as follows:
, we note that our model (13) is the AA-model [18] as follows:

Borrowing the idea of [6], we dynamically compute the value of  according to the variance of the recovered noise which matches that of our prior knowledge. The Gamma-distributed noise has the mean and variance as follows:
according to the variance of the recovered noise which matches that of our prior knowledge. The Gamma-distributed noise has the mean and variance as follows:

The solution procedure uses a parabolic equation with time as an evolution parameter. This means that we solve

for  . We merely multiply the first equation of (33) by
. We merely multiply the first equation of (33) by  and integrate by parts over
and integrate by parts over  . If steady state has been reached, the left side of the first equation of (33) vanishes, and then we have
. If steady state has been reached, the left side of the first equation of (33) vanishes, and then we have

Then, we determine the best value of  from their tested values such that the peak signal-to-noise ratio (PSNR, see definition here in after) of the restored image is the maximal.
from their tested values such that the peak signal-to-noise ratio (PSNR, see definition here in after) of the restored image is the maximal.
3.3. Other Methods
We have compared our results with some other variational multiplicative denoising methods.
RLO Method. The solution of RLO-model [17] is obtained by using the following gradient projection iterative scheme [17] (the subscripts  are omitted):
are omitted):

In our experiments,  and time step size
and time step size  are set to be
are set to be  and 0.2, respectively. The two Lagrange multipliers
and 0.2, respectively. The two Lagrange multipliers  and
and  are dynamically updated to satisfy the constraints (as explained in [17]).
are dynamically updated to satisfy the constraints (as explained in [17]).
AA Method. The solution of AA-model [18] is obtained by using the gradient projection method:

In our experiments,  take the same value in the RLO method. The regularization parameter
take the same value in the RLO method. The regularization parameter  is dynamically updated according to (34).
is dynamically updated according to (34).
HMW Method. The solution of HMW-model [20] (we note that HMW-model is equivalent to SO-model as  .)
.)

is obtained by using the following alternating minimization algorithm:

The corresponding nonlinear Euler-Lagrange equation of  -subproblem of (3.12)
-subproblem of (3.12)

was solved by using the Newton method. The Chambolle projection algorithm was employed in the denoising  -subproblem of (3.12) [20]. Then the restored image is computed by
-subproblem of (3.12) [20]. Then the restored image is computed by  . Here, the rule to determine the two regularization parameters
. Here, the rule to determine the two regularization parameters  and the stopping criterion of the HMW method are chosen as suggested in [20].
and the stopping criterion of the HMW method are chosen as suggested in [20].
In our computational experiments, we use the initial guess  in RLO and AA method and
in RLO and AA method and  in HMW method. RLO and AA algorithms are terminated once they reached maximal PSNR.
in HMW method. RLO and AA algorithms are terminated once they reached maximal PSNR.
3.4. Denoising of Color Images
In this subsection, we extend our approach to solve the multichannel version of (13). The general framework of the variational approach for color images processing based on the linear RGB color models can be classified into two categories—the channel-by-channel approach and the vectorial approach. Compared with the first approach, the second approach can exploit the spatial correlation and the spectral correlation in processing color images. So the vectorial approach has already been used in most of the literature for RGB images, such as the work of [31–33] solved multichannel total variation (MTV) regularization reconstruction problem. Considering that our multiplicative denoising variational model includes the Weberized TV regularizer, we choose the channel-by-channel approach in this paper for color image multiplicative noise removal due to its simplicity and robustness.
Recently, Zhang et al. [5] proposed an additive denoising scheme by using principal component analysis (PCA) with local pixel grouping (LPG). We refer to this method as LPG-PCA method. For a better preservation of image local structures, a pixel and its nearest neighbors are modeled as a vector variable, whose training samples are selected from the local window by using block matching-based LPG. The LPG-PCA denoising procedure is iterated one more time to further improve the denoising performance, and the noise level is adaptively adjusted in the second stage.
In our experiments, we only compare the denoising results of the noisy color images obtained by our approach with those obtained by the LPG-PCA method. We do it for the following two reasons: first, the LPG-PCA method using the channel-by-channel approach has been extended to solve the color image denoising problem; second, the multiplicative noise can be converted into additive noise by logarithmic transformation. In the LPG-PCA method, we make the size of the variable block and training block 2 and 20, respectively. We use  as the initial guess. Then, the restored image is computed by exponential transform.
as the initial guess. Then, the restored image is computed by exponential transform.
3.5. Results
The six test images (size:  ) used in the experiments, including five grey level images and one color image, are shown in Figures 1(a)–6(a) and Figures 9(a)–10(a), respectively. In our tests, each pixel of an original image is degraded by a noise which follows a Gamma distribution with density function in (3) and
) used in the experiments, including five grey level images and one color image, are shown in Figures 1(a)–6(a) and Figures 9(a)–10(a), respectively. In our tests, each pixel of an original image is degraded by a noise which follows a Gamma distribution with density function in (3) and  is specified to have mean 1 and standard deviation
is specified to have mean 1 and standard deviation  . The noise level is controlled by the value of
. The noise level is controlled by the value of  in the experiments. The noisy images with different levels (
in the experiments. The noisy images with different levels ( ) are shown in Figures 1(b)–6(b) and Figures 9(b)–10(b), respectively. We display the denoising results obtained by our approach as well as by the RLO, AA, HMW, and LPG-PCA methods.
) are shown in Figures 1(b)–6(b) and Figures 9(b)–10(b), respectively. We display the denoising results obtained by our approach as well as by the RLO, AA, HMW, and LPG-PCA methods.
We measure the quality of restoration by the peak signal-to-noise ratio (PSNR), the improved signal-to-noise ratio (ISNR), and the relative error (ReErr) of the restored image, defined by

where  are the original, the restored, the observed image, and the size of the image, respectively.
are the original, the restored, the observed image, and the size of the image, respectively.
Figures 1–6 show the denoising results of the six noisy gray level images by different methods. The subfigures (c–f) are the denoised images by the different methods. In these experiments, it is clear that the restoration results obtained by the proposed method are visually better than those by the HMW, AA, and RLO methods, especially when the noise variance is large, that is, when  is small. Although the most denoised images by the HMW method have better visual quality, we note that some details, such as camera and buildings in Figure 3(e), become hazy. Such hazy details make the reconstructed image visually unpleased in some areas. Next we check the homogeneity of regions of interest in the image and analyze the loss (or the preservation) of contrast. In Figures 7 and 8, we show several lines of the original, noisy, and restored images. It is clear from the figures that the lines restored by the proposed method are better than those restored by the other three methods.
is small. Although the most denoised images by the HMW method have better visual quality, we note that some details, such as camera and buildings in Figure 3(e), become hazy. Such hazy details make the reconstructed image visually unpleased in some areas. Next we check the homogeneity of regions of interest in the image and analyze the loss (or the preservation) of contrast. In Figures 7 and 8, we show several lines of the original, noisy, and restored images. It is clear from the figures that the lines restored by the proposed method are better than those restored by the other three methods.
Table 1 lists the PSNR, ISNR, and ReErr results by different methods on the six noisy gray level images. From Table 1, we can see that the PSNRs and ISNRs of the images restored by using our method are more than those restored by using the other three methods, and ReErrs are less than the other four methods, except for the denoising results of Figure 4(b) obtained by the HMW method. In addition to the quality of the restored images, we also find that the proposed algorithm is efficient. Table 2 shows the number of iterations and the computational times required by the different algorithms. From Table 2, we see that the RLO algorithm takes more time than the other three methods. The spending time of our algorithm is in a middle position in comparison with the other three methods.
We now compare the LPG-PCA method with the proposed method on denoising the noisy color images. Figures 9–10 show the denoising results by the two methods. Table 3 lists the PSNR, ISNR, and ReErr results, the number of iterations, and the computational times of the two algorithm. We see that although LPG-PCA method has the lower PSNR and ISNR measures and higher ReErrs than our method, their denoised images have better visual quality. The LPG-PCA method well preserves the image edges without introducing staircase effect. However, staircase effect is an innate defect of the TV regularization method. From Table 3, we also see that the LPG-PCA method consumes much time than our method to obtain comparable good images.
4. Conclusion
In this paper, we have studied a new nonconvex variational model for multiplicative noise removal under MAP framework. Then we prove the existence and uniqueness of a minimizer for the new model. Moreover, we develop an iterative algorithm based on the linearization technique for the associated nonlinear Euler-Lagrange equation and we demonstrate the good performance of the model on some numerical results. In the future, we will focus on resolving the two remaining problems. First, we will prove the uniqueness issue of the proposed model using the  instead of
instead of  in
in  . Second, we will give the convergence proof of our algorithm.
. Second, we will give the convergence proof of our algorithm.
References
Donoho DL, Johnstone M: Adapting to unknown smoothness via wavelet shrink-age. Journal of the American Statistical Association 1995,90(432):1200-1224. 10.2307/2291512
Bao P, Zhang L: Noise reduction for magnetic resonance images via adaptive multiscale products thresholding. IEEE Transactions on Medical Imaging 2003,22(9):1089-1099. 10.1109/TMI.2003.816958
Geman S, Geman D: Stochastic relaxation, Gibbs distributions, and the Bayesian restoration of images. IEEE Transactions on Pattern Analysis and Machine Intelligence 1984,6(6):721-741.
Zhang L, Lukac R, Wu X, Zhang D: PCA-based spatially adaptive denoising of CFA images for single-sensor digital cameras. IEEE Transactions on Image Processing 2009,18(4):797-812.
Zhang L, Dong W, Zhang D, Shi G: Two-stage image denoising by principal component analysis with local pixel grouping. Pattern Recognition 2010,43(4):1531-1549. 10.1016/j.patcog.2009.09.023
Rudin LI, Osher S, Fatemi E: Nonlinear total variation based noise removal algorithms. Physica D 1992,60(1–4):259-268.
Aubert G, Kornprobst P: Mathematical Problems in Image Processing, Applied Mathematical Sciences. Volume 147. Springer, Berlin, Germany; 2002.
Buades A, Coll B, Morel JM: A review of image denoising algorithms, with a new one. Multiscale Modeling and Simulation 2005,4(2):490-530. 10.1137/040616024
Lewis H: Principle and Applications of Imaging Radar, Manual of Remote Sensing. Volume 2. 3rd edition. John Wiley & Sons, New York, NY, USA; 1998.
Lee JS: Digital image enhancement and noise filtering by use of local statistics. IEEE Transactions on Pattern Analysis and Machine Intelligence 1980,2(2):165-168.
Kuan DT, Sawchuk AA, Strand TC, Chavel P: Adaptive noise smoothing filter for images with signal-dependent noise. IEEE Transactions on Pattern Analysis and Machine Intelligence 1985,7(2):165-177.
Yu Y, Acton ST: Speckle reducing anisotropic diffusion. IEEE Transactions on Image Processing 2002,11(11):1260-1270. 10.1109/TIP.2002.804276
Aja-Fernández S, Alberola-López C: On the estimation of the coefficient of variation for anisotropic diffusion speckle filtering. IEEE Transactions on Image Processing 2006,15(9):2694-2701.
Krissian K, Westin C-F, Kikinis R, Vosburgh KG: Oriented speckle reducing anisotropic diffusion. IEEE Transactions on Image Processing 2007,16(5):1412-1424.
Liu G, Zeng X, Tian F, Li Z, Chaibou K: Speckle reduction by adaptive window anisotropic diffusion. Signal Processing 2009,89(11):2233-2243. 10.1016/j.sigpro.2009.04.042
Deledalle CA, Denis L, Tupin F: Iterative weighted maximum likelihood denois-ing with probabilistic patch-based weights. IEEE Transactions on Image Processing 2009,18(12):2661-2672.
Rudin LI, Lions PL, Osher S: Multiplicative denoising and deblurring: theory andalgorithms. In Geometric Level Set Methods in Imaging, Vision, and Graphics. Edited by: Osher S, Paragios N. Springer, Berlin, Germany; 2003:103-120.
Aubertt G, Aujol J-F: A variational approach to removing multiplicative noise. SIAM Journal on Applied Mathematics 2008,68(4):925-946. 10.1137/060671814
Shi J, Osher S: A nonlinear inverse scale space method for a convex multiplicative noise model. SIAM Journal on Imaging Sciences 2008,1(3):294-321. 10.1137/070689954
Huang YM, Ng MK, Wen YW: A new total variation method for multiplicativenoise removal. SIAM Journal on Imaging Sciences 2009,2(1):22-40.
Bioucas DJ, Figueiredo M: Total variation restoration of speckled images using a split-Bregman algorithm. Proceedings of IEEE International Conference on Image Processing (ICIP '2009), 2009, Cairo, Egypt
Steidl G, Teuber T: Removing multiplicative noise by douglas-rachford splitting methods. Journal of Mathematical Imaging and Vision 2010,36(2):168-184. 10.1007/s10851-009-0179-5
Durand S, Fadili J, Nikolova M: Multiplicative noise cleaning via a variational methodinvolving curvelet coe±cients. In Scale Space and Variational Methods. Edited by: Lie A, Lysaker M, Morken K, Tai X-C. Springer, Voss, Norway; 2009.
Shen J: On the foundations of vision modeling: I. Weber's law and Weberized TV restoration. Physica D 2003,175(3-4):241-251. 10.1016/S0167-2789(02)00734-0
Shen J, Jung Y-M: Weberized mumford-shah model with bose-einstein photon noise. Applied Mathematics and Optimization 2006,53(3):331-358. 10.1007/s00245-005-0850-1
Wei Z, Fu Y, Gao Z, Cheng S: Visual compander in wavelet-based image coding. IEEE Transactions on Consumer Electronics 1998,44(4):1261-1266. 10.1109/30.735825
Wei ZH, Qin P, Fu YQ: Perceptual digital watermark of images using wavelet transform. IEEE Transactions on Consumer Electronics 1998,44(4):1267-1272. 10.1109/30.735826
Weber EH: De pulsu, resorptione, audita et tactu. In Annotationes anatomicae et physio-logicae. Koehler, Leipzig, Germany; 1834.
Vogel CR, Oman ME: Iterative methods for total variation denoising. SIAM Journal of Scientific Computing 1996,17(1):227-238. 10.1137/0917016
Chan TF, Osher S, Shen J: The digital TV filter and nonlinear denoising. IEEE Transactions on Image Processing 2001,10(2):231-241. 10.1109/83.902288
Yang J, Yin W, Zhang Y, Wang Y: A fast algorithm for edge-preserving variationalmultichannel image restoration. SIAM Journal on Imaging Sciences 2009,2(1):569-592.
Brook A, Kimmel R, Sochen NA: Variational restoration and edge detection for color images. Journal of Mathematical Imaging and Vision 2003,18(3):247-268. 10.1023/A:1022895410391
Chan T, Shen J: Variational restoration of nonflat image features: models and algorithms. SIAM Journal on Applied Mathematics 2000,61(4):1338-1361.
Mallat S: A Wavelet Tour of Signal Processing. Academic Press, New York, NY, USA; 1999.
Combettes PL, Wajs VR: Signal recovery by proximal forward-backward splitting. Multiscale Modeling and Simulation 2005,4(4):1168-1200. 10.1137/050626090
Acknowledgments
The authors thank the authors of [5, 20] for sharing their programs. Moreover, they would like to express their gratitude to the anonymous referees and editor for making helpful and constructive suggestions. This work was supported in part by the Natural Science Foundation of China under Grant nos. 60802039 and 60672074, by the National 863 High Technology Development Project under Grant no. 2007AA12Z142, by the Doctoral Foundation of Ministry of Education of China under Grant no. 200802880018, and by the Scientific Innovation project of Nanjing University of Science and Technology no. 2010ZDJH07.
Author information
Authors and Affiliations
Corresponding author
Appendix
Proof of Theorems 1 and 2
To prove the existence Theorem 1, we first give a Maximum Principle type result for the energy form (13).
Lemma A.3.
Suppose that  with
with  ; the solution
; the solution  of the problem (13) has the following property:
of the problem (13) has the following property:


Proof.
The similar assertion appears in [18]; we detail the argument for completeness. Let  , and
, and  . We remark that
. We remark that  is strictly increasing for
is strictly increasing for  . Hence, we have that
. Hence, we have that


Moreover, we have that (see [34, Lemma  in Section
in Section  ], [21, Lemma
], [21, Lemma  in Section
in Section  ])
])


Therefore we deduce that


and the equality holds if and only if  , a.e. Since
, a.e. Since  is a minimizer in
is a minimizer in  , the equality must hold and thus
, the equality must hold and thus  , a.e. We get in the same way that
, a.e. We get in the same way that


and thus  .
.
Based on aforementioned lemma, now we are ready to give the proof of Theorem 1.
Proof of Theorem 1.
Without loss of generality, we assume that  . Applying ideas in [24], let us denote that
. Applying ideas in [24], let us denote that  . We note that the admissible space
. We note that the admissible space  is nonempty since
is nonempty since  . Let
. Let  be a minimizing sequence for problem (13). Thanks to Lemma 2, we can assume that
be a minimizing sequence for problem (13). Thanks to Lemma 2, we can assume that  . This implies that
. This implies that  is bounded (
is bounded ( is bounded).
is bounded).
For a sequence  , we have
, we have  , where
, where  is a constant. Since
is a constant. Since  and
and  reaches its minimum value
reaches its minimum value  when
when  , we get that
, we get that  is bounded in
is bounded in  .
.
Thus, up to a subsequence, there exists u in  such that
such that  in
in  -strong. Furthermore, after a refinement of the subsequence if necessary, we can assume that
-strong. Furthermore, after a refinement of the subsequence if necessary, we can assume that


Using the Lebesgue Dominated Convergence Theorem, then we have


Next we prove that  is lower semicontinuity. Firstly, from the properties of the
is lower semicontinuity. Firstly, from the properties of the  [7], we have
[7], we have


Secondly, the lower semicontinuity of Weberized TV can also be proved. Let us define  and
and  ; then
; then


Let  be a vector-valued function such that
be a vector-valued function such that  . We have
. We have


and also


Since  is compactly supported, the right side of the above inequality belongs to
is compactly supported, the right side of the above inequality belongs to  . Therefore, again by the Lebesgue Dominated Convergence Theorem,
. Therefore, again by the Lebesgue Dominated Convergence Theorem,


Now take sup over  to get
to get


Combining (A.1), (A.2), and (A.3), we have


It is easy to see that  . Since
. Since  is a minimizing sequence, we therefore have shown that
is a minimizing sequence, we therefore have shown that  is in fact a minimizer.
is in fact a minimizer.
Based on the theory of optimization, an objective function possesses a unique minimizer when it is strictly convex and coercive [35]. Since the negative log-likelihood and Weberized TV prior are not convex, as a result, the restoration energy  in (13) is not convex and uniqueness is no longer a direct product of convexity. We address the problem of the uniqueness of the solution of problem (13), which relies on the formal Euler-Lagrange equation of (13):
in (13) is not convex and uniqueness is no longer a direct product of convexity. We address the problem of the uniqueness of the solution of problem (13), which relies on the formal Euler-Lagrange equation of (13):
Proof of Theorem 2.
Let us denote


Define a new reference energy  for the restoration energy
for the restoration energy  as follows:
as follows:


It is easy to derive that (23) is exactly the Euler-Lagrange equilibrium equation for  . We have
. We have


We deduce that if (18) holds, then  and
and  is strictly convex. Now that the TV Radon measure is semiconvex, so the objective function
is strictly convex. Now that the TV Radon measure is semiconvex, so the objective function  is globally strictly convex and possesses a unique minimizer.
is globally strictly convex and possesses a unique minimizer.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License ( https://creativecommons.org/licenses/by/2.0 ), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Huang, LL., Xiao, L. & Wei, ZH. Multiplicative Noise Removal via a Novel Variational Model. J Image Video Proc 2010, 250768 (2010). https://doi.org/10.1155/2010/250768
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1155/2010/250768
 , this reduces to the SO-model [
, this reduces to the SO-model [ .
.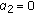 , this reduces to the AA-model [
, this reduces to the AA-model [
 ; denoised images by (c) RLO method; (d) AA method; (e) HMW method
; denoised images by (c) RLO method; (d) AA method; (e) HMW method  ; (f) the proposed method
; (f) the proposed method  .
.
 ; denoised images by (c) RLO method; (d) AA method; (e) HMW method
; denoised images by (c) RLO method; (d) AA method; (e) HMW method  ; (f) the proposed method
; (f) the proposed method  .
.
 ; denoised images by (c) RLO method; (d) AA method; (e) HMW method
; denoised images by (c) RLO method; (d) AA method; (e) HMW method  ; (f) the proposed method
; (f) the proposed method  .
.
 ; denoised images by (c) RLO method; (d) AA method; (e) HMW method
; denoised images by (c) RLO method; (d) AA method; (e) HMW method  ; (f) the proposed method
; (f) the proposed method  .
.
 ; denoised images by (c) RLO method; (d) AA method; (e) HMW method
; denoised images by (c) RLO method; (d) AA method; (e) HMW method  ; (f) the proposed method
; (f) the proposed method  .
.
 ; denoised images by (c) RLO method; (d) AA method; (e) HMW method
; denoised images by (c) RLO method; (d) AA method; (e) HMW method  ; (f) the proposed method
; (f) the proposed method  .
.


 ; denoised images by (c) LPG-PCA method; (d) the proposed method
; denoised images by (c) LPG-PCA method; (d) the proposed method  .
.
 ; denoised images by (b) LPG-PCA method; (c) the proposed method
; denoised images by (b) LPG-PCA method; (c) the proposed method  .
.